5.2. Математический маятник

Математический маятник – это материальная точка на длинной невесомой нерастяжимой нити.

; (5.17)

F = mgsin. (5.18)

При малых колебаниях маятника

(5.19)

Тогда . (5.20)

Сила не упругая по своей природе, но она, как и упругая сила, направлена к положению равновесия и возрастает при увеличении смещения от положения равновесия. Такая сила называется квазиупругой (почти упругой).

Запишем для математического маятника II закон Ньютона для вращающегося тела:

, (5.21)

где - момент инерции материальной точки, - угловое ускорение; - момент силы тяжести.

В проекции на ось вращения, проходящую через точку подвеса маятника, это уравнение имеет вид:

, обозначение , ;

(если ).

Это дифференциальное уравнение имеет решения, аналогичные (5.7):

,

.

Значит, при малых отклонениях от положения равновесия колебания математического маятника являются гармоническими. Период колебаний математического маятника

. (5.22)

5.3. Свободные незатухающие электромагнитные колебания

Электромагнитные колебания – это периодические изменения с течением времени электрических и магнитных величин: q – заряда, I – силы тока; - напряженности электрического поля; - магнитной индукции; - энергии электрического поля; - энергии магнитного поля и т.д.

С вободные незатухающие электромагнитные колебания можно получить в колебательном контуре, не обладающем активным сопротивлением R (рис. 5.4).

, (5.23)

где q – заряд на обкладках конденсатора.

, (5.24)

где I – сила тока, .

Поскольку потери энергии на джоулево тепло отсутствуют, полная энергия контура остается постоянной:

, (5.25)

а ее производная по времени равна нулю:

; .

Найдем производную по времени от полной энергии контура:

; .

Обозначим:

.

Тогда последнее уравнение приобретает вид

. (5.26)

Это дифференциальное уравнение описывает зависимость заряда на обкладках конденсатора от времени. Оно аналогично (5.6). Колебания заряда являются свободными гармоническими. Они описываются уравнениями, аналогичными (5.7):

или .

Период свободных электромагнитных колебаний:

. (5.27)

- (5.28)

- зависимость от времени силы тока в контуре.

- (5.29)

- зависимость от времени разности потенциалов на обкладках конденсатора.

- (5.30)

- зависимость от времени энергии электрического поля.

- (5.31)

- зависимость от времени энергии магнитного поля.

5.4. Сложение гармонических колебаний, происходящих в одном направлении с одинаковой частотой

Гармонические колебания можно представить на векторной диаграмме с помощью вектора, длина которого равна амплитуде колебаний, а угол, образованный этим вектором с положительным направлением оси x в начальный момент времени, равен начальной фазе колебаний.

При вращении конца этого вектора относительно т. 0 с угловой скоростью его проекция на ось x меняется по закону .

Пусть складываются два колебания:

, (5.32)

. (5.33)

Результирующим движением будет гармоническое колебание, происходящее с той же частотой , в том же направлении, что и складываемые колебания. Амплитуда и начальная фаза результирующего колебания определяются соотношениями:

, (5.34)

. (5.35)

Уравнение результирующего колебания имеет вид:

. (5.36)

Пусть амплитуды двух колебаний, происходящих в одном направлении, равны, а частоты мало отличаются.

, (5.37)

, (5.38)

причем ; .

Рассмотрим результат сложения этих колебаний:

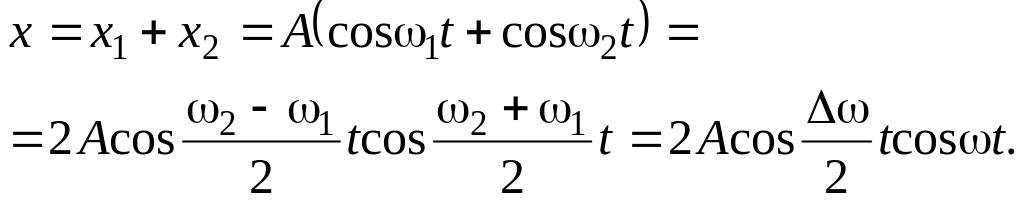(5.39)

Видно, что амплитуда этого колебания меняется с течением времени по гармоническому закону

. (5.40)

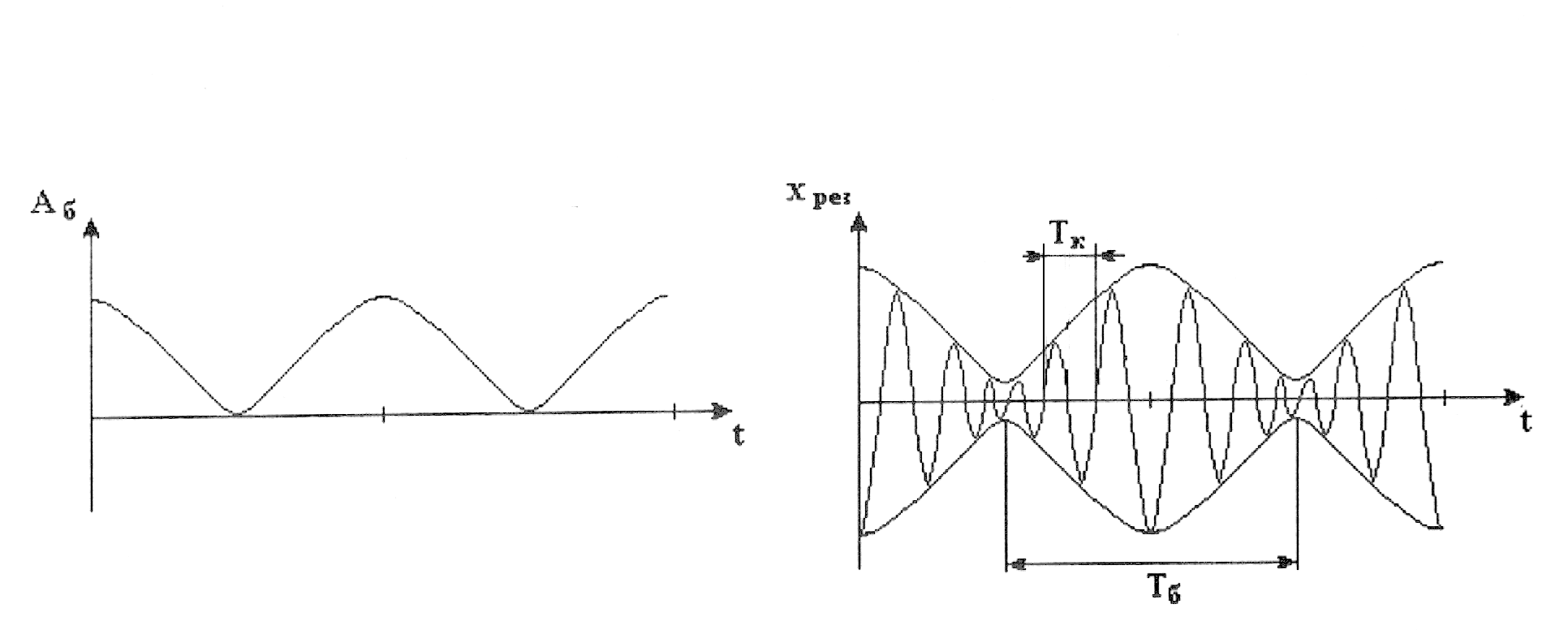
Рис. 5.7

Рис. 5.8

Результирующее колебание называется в этом случае биением.

, (5.41)

где - амплитуда биений;

- частота биений;

- частота колебаний;

- период биений;

- период колебаний.