Метод половинного деления

Пусть при решении задачи (1) определен отрезок [a, b], которому принадлежит точка локального минимума х*, и функция f(x) является унимодальной на этом отрезке.

Далее для сужения отрезка унимодальности используем точки х₁ и х₂, расположенные симметрично относительно середины отрезка [a, b];

Будем считать, что число k гораздо меньше 1 (k << 1). Тогда точки х₁ и х₂ принадлежат отрезку [a, b] и, следуя рассмотренной в прошлом пункте схеме, получим новый суженный отрезок [a₁, b₁] и оценим его длину в каждом из трех возможных случаев:

I. y₁ < y₂, a₁ = a, .

II. y₁ > y₂, .

III. y₁ = y₂, a₁ = x₁, b₁=x₂;

Таким образом, после первого шага преобразований найден новый отрезок унимодальности [a₁, b₁], длина которого уменьшилась.

Название метода (метод половинного деления) мотивировано тем, что если величина k очень мала, то длина отрезка унимодальности b-а уменьшается почти вдвое (в случаях I, II).

Теперь в новом суженном промежутке [а₁, b₁] выберем точки и , симметричные относительно его середины:

.

Проведя вычисления, аналогичные проделанным ранее, получаем отрезок [а₂, b₂], длина которого не больше

,

и т. д.

В результате приходим к последовательности таких вложенных отрезков [a, b], [a₁, b₁] … [а_n, b_n], …, что точка локального минимума х* функции f(x) принадлежит каждому из них и является общим пределом последовательностей {а_n} и {b_n}. Отсюда получаются приближенные равенства

х*  a_n  b_n,

точность которых на n-м шаге вычислений можно оценить неравенством

(2)

Пример 3. Найти точку х* локального минимума функции f(х) = 2x² – ln x на отрезке [0,25; 1] методом половинного деления с точностью  = 0,1. Провести вычисления, полагая k = 0,1 и предварительно оценив минимальное число шагов n для достижения точности .

Решение. Было установлено (см. пример 1), что функция унимодальна на отрезке [0,25;1]; точка х* принадлежит этому отрезку. Воспользуемся неравенством (2) и определим число шагов n:

Обозначим

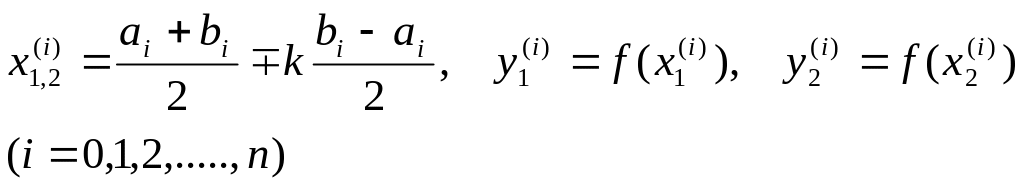(3)

где a₀ = a = 0,25, b₀ = b = 1, a_i, b_i - координаты начала и конца отрезка, полученные на i-м шаге вычислений, точки и принадлежат отрезку [a_i, b_i].

Произведем последовательные вычисления.

Отрезок [a,b] = [0,25; 1]:

x₁ = 0,5375, х₂ = 0,6625, у₁ = 1,2221 < у₂ = -1,2895.

Отрезок [а₁, b₁] = [а, х₂] = [0,25; 0,66251]:

= 0,4356, = 0,4769, = 1,2105 > = 1,1953.

Отрезок [а₂, b₂] = [ , x₂] = [0,4356; 0,66251];

= 0,5377, = 0,5604, = 1,1987 < = 1,2072.

Отрезок [a₃,b₃] = [ , ] = [0,4356; 0,56041]:

= 0,4918, = 0.5043, = 1,1934 > = 1,1932.

Отрезок [a₄, b₄] = [ , ] = [0,4918; 0,5604].

Разность  = b₄ - а₄ = 0.0686 < =0,1. Следовательно, точкой локального минимума, найденной с заданной точностью, является х*  а₄ = 0,4918.

Метод золотого сечения

Термин «золотое сечение» ввел Леонардо да Винчи. Точка х₁ является золотым сечением отрезка [а, b], если отношение длины b-а всего отрезка к длине b-х₁ большей части равно отношению длины большей части к длине х₁-а меньшей части (рис. 3), т.е. х₁ - золотое сечение, если справедливо отношение

Аналогично, точка х₂, симметричная точке х₁ относительно середины отрезка [а, b], является вторым золотым сечением этого отрезка. Так как точки х₁ и х₂ расположены симметрично относительно середины отрезка [а, b], то можно записать

(4)

Учитывая, что , и используя определение золотого сечения, вычислим число k > 0:

.

Отметим свойство золотого сечения, в котором легко убедиться: пусть x₁ и х₂ - два золотых сечения отрезка [а, b]; тогда точка х₁ одновременно является золотым сечением отрезка [а, х₂], а другая точка х₂ - золотым сечением отрезка [х₁, b] (рис. 3).

Т еперь разберем подробнее алгоритм метода золотого сечения при нахождении последовательности вложенных отрезков [a_i, b_i] (i=0, 1, ... , n), сужающихся к точке х* локального минимума унимодальной функции f(x).

Сначала на исходном отрезке [а, b] по формулам (4) при найдем точки х₁ и х₂, а затем разность ₁x = х₂ – х₁. Далее вычисляем значения функции у₁=f(х₁) и у₂=f(х₂) и, следуя схеме, описанной выше, образуем суженный отрезок [а₁, b₁]. Наконец, готовясь к следующему шагу и используя свойство золотого сечения, на отрезке [а₁, b₁] находим два сечения и . При этом возможны три случая:

1. .

2. .

3. .

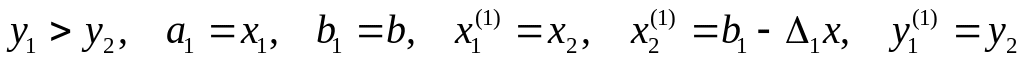Теперь, следуя разобранной схеме, можно переходить к нахождению отрезков [а₂, b₂], [а₃, b₃] и т. д., учитывая при этом, что в случаях I или II значение или целевой функции уже получено на предыдущем шаге (i = 1,2,...,n).

Точность приближенного равенства х*  а_n  b_n на n-м шаге вычислений можно оценить неравенством

(5)

полученным из неравенства (2), где .

Пример 4. Найти точку х* локального минимума функции f(x) = 2х²-ln х на отрезке [0,25; 1] методом золотого сечения с точностью  = 0,1. Провести вычисления, предварительно оценив минимальное число шагов n для достижения точности .

Решение. Определим минимальное число шагов n, используя неравенство (5):

Произведем последовательные вычисления.

Отрезок [a,b] = [0,25; 1]:

x₁ = 0,5375, х₂ = 0,7135, у₁ = 1,1983 < у₂ = 1,3558, x₁ = 0,177.

Отрезок [а₁, b₁] = [а, х₂] = [0,25; 0,7135]:

= 0,4271, = x₁, = 1,2156 > = y_1, x₂ = 0,1094.

Отрезок [а₂, b₂] = [ , x₂] = [0,4271; 0,7135];

= = x₁, = 0,6041, = y₁ < = 1,2339, x₃ = 0,06763.

Отрезок [a₃,b₃] = [ , ] = [0,4271; 0,6041]:

= 0,4947, = = = x₁, = 1,1933 < = y₁, x₄ = 0,0418.

Отрезок [a₄, b₄] = [ , ] = [0,4271; 0.5365];

= 0,4688, = , = 1,1971 > = , x₅ = 0,0258.

Отрезок [a₅, b₅] = [ , ] = [0,4688; 0.5365];

Точкой минимума функции f(x) с погрешностью  = b₅ – а₅ = 0.0677 < 0,1 =  является х*  а₅ = 0,4688.