4.6. Інтеґрування тригонометричних функцій

В цьому пункті ми роглядаємо деякі методи інтеґрування функції

, ( 2 )

яка є раціональною функцією двох арґументів , .

4.6.1. Універсальна тригонометрична підстановка

Теорема 3. Інтеґрування функції (2) завжди зводиться до інтеґрування раціональної функції однієї змінної t за допомогою так званої універсальної тригонометричної підстановки (УТП)

( 3 )

■На підставі (3) ми маємо

,

,

.

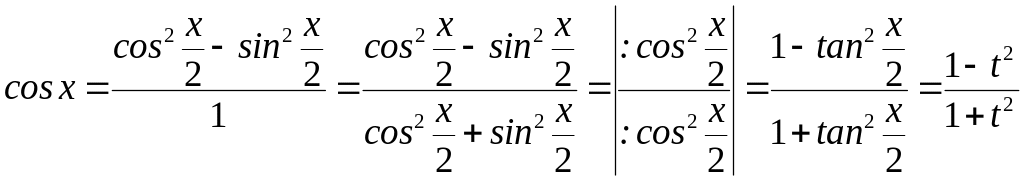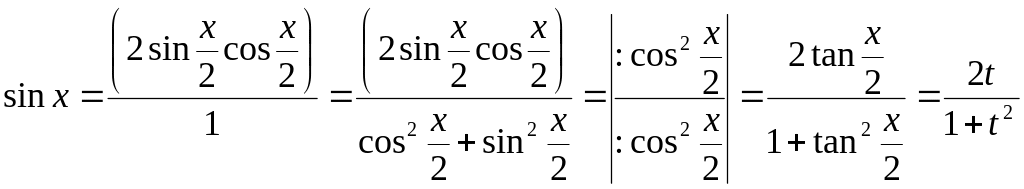отже,

, ( 4 )

і

,

де функція арґументу t

є раціональною.■

Приклад 6. Використовуючи УТП, маємо

.

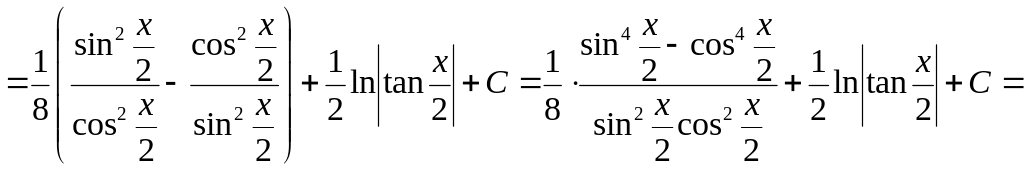
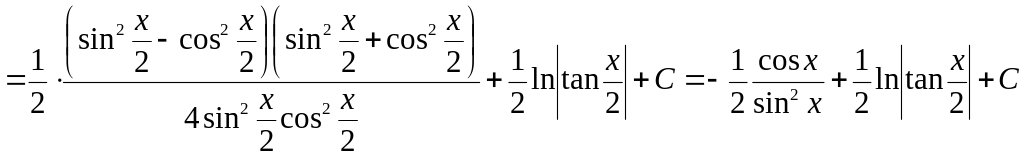Зауважимо, що застосування УТП до схожого інтеґрала

не дає нічого доброго, бо веде до надзвичайно громіздкого раціонального дробу. Дійсно,

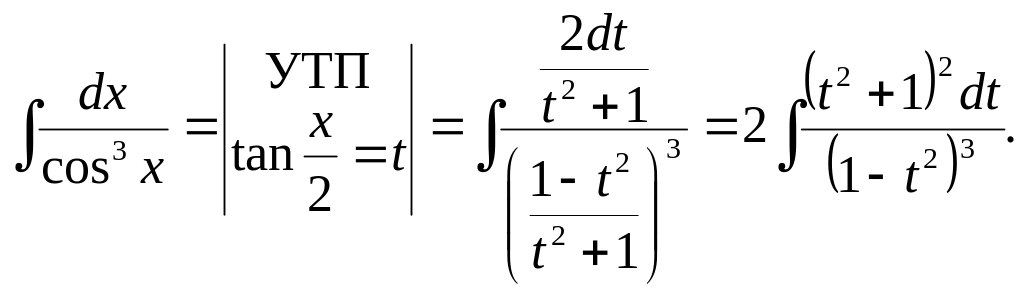
Приклад 7. Для обчислення інтеґрала

можна звести його до попереднього інтеґрала заміною змінної, а саме:

,

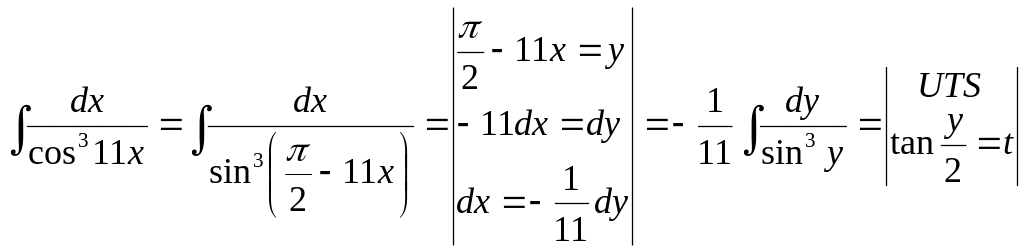і далі діяти як в попередньому прикладі.

Приклад 8.

.

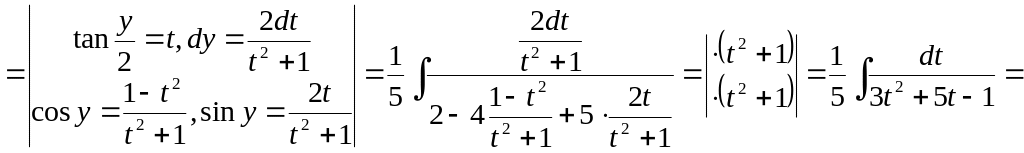
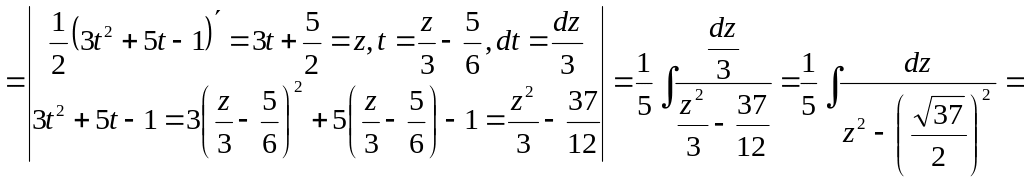
4.6.2. Інші підстановки

I. Якщо функція (2) непарна відносно , тобто

, ( 5 )

то її можна перетворити до вигляду:

,

де - раціональна функція однієї змінної . Заміна

( 6 )

зводить інтеґрування до інтеґрування рациінальної функції від t.

II. Якщо функція (2) є непарною відносно , тобто

, ( 7 )

то її можна звести до вигляду

( - раціональна функція арґумену ) і застосувати підстановку

( 8 )

III. Якщо функція (2) є парною відносно сукупності обох арґументів і , тобто

( 9 )

то її можна привести до раціональної функції від ,

,

и проінтеґрувати за допомоги однієї з підстановок

. ( 10 )

Приклад 9. Обчислити невизначений інтеґрал

.

Підінтеґральна функція непарна відносно , бо

,

і тому маємо справу з випадком І, коли підінтеґральна функція перетворюється в добуток на функцію від . Можна діяти наступним чином:

.

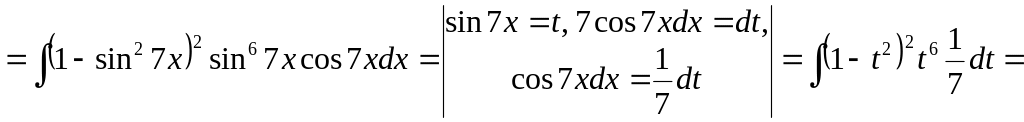
Приклад 10. Підінтеґральна функція невизначеного інтеґрала

непарна відносно і тому, згідно з випадком ІІ, перетворюється в добуток на функцію від з наступною заміною змінної . Маємо

.

Приклад 11. Обчислити інтеґрал

.

Переходячи від котанґенса до танґенса, діємо відповідно до випадку ІІІ.

.

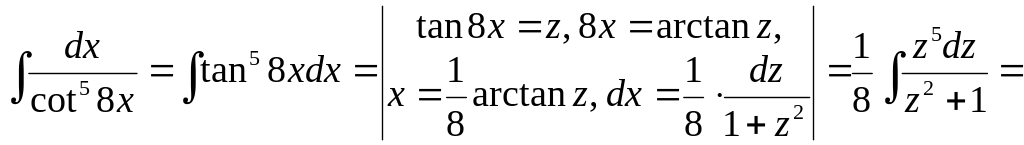
Приклад 12. Обчисліть самостійно інтеґрал

.

Вказівка. Перейдіть до котанґенса і покладіть .

Приклад 13. Знайти невизначений інтеґрал

.

Ми маємо справу з випадком ІІІ, і тому можемо перетворити підінтеґральну функцію в функцію від . Ми зробимо ще краще – перетворимо її в добуток функції від на похідну від . Отримаємо

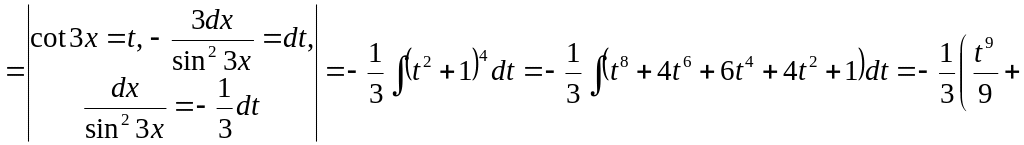
Приклад 14. Невизначений інтеґрал

також можна обчислювати відповідно до випадку ІІІ, оскільки підінтеґральна функція

є парною по сукупності обох арґументів и , тобто

.

Перетворюючи підінтеґральну функцію в добуток функції від на похідну від , отримуємо

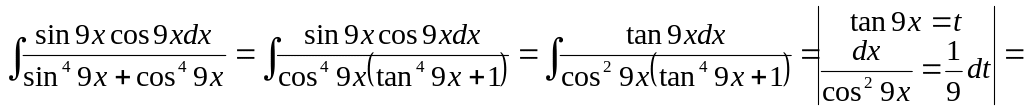
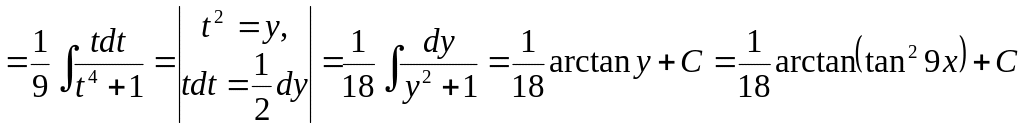
Зауваження. Зазначені підстановки можуть бути застосовними до деяких ірраціональніх функцій від і .

Приклад 15.

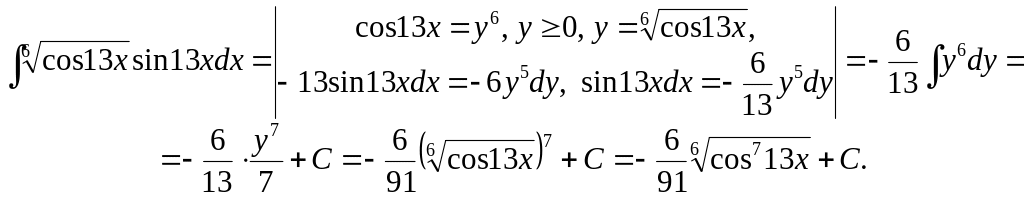
Приклад 16. Для додатних

.
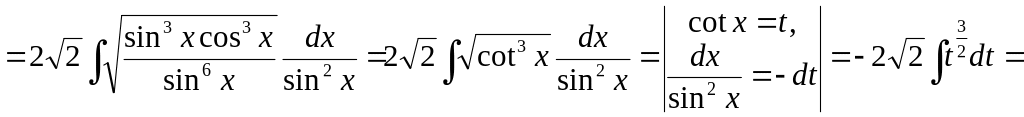