
- •Частина друга: інтеґральне числення. Диференціальні рівняння. Ряди
- •4.1.2. Властивості первісної
- •4.2. Невизначений інтеґрал
- •4.2.1. Означення невизначеного інтеґрала
- •4.2.2. Властивості невизначеного інтеґрала
- •4.3. Інтеґрування підстановкою (заміна змінної)
- •4.4. Інтеґрування частинами
- •4.5. Інтеґрування раціональних дробів та функцій
- •4.6. Інтеґрування тригонометричних функцій
- •4.6.1. Універсальна тригонометрична підстановка
- •4.6.2. Інші підстановки
- •4.6.3. Деякі інші методи а) Застосування формул зниження степеня
- •Б) Застосування формул перетворення добутку тригонометричних функцій в алгебричну суму
- •4.7. Інтеґрування ірраціональних функцій
- •4.7.1. Линійні і дробово-лінійні ірраціональності
- •4.7.2. Квадратичні ірраціональності. Тригонометричні підстановки
- •4.7.3. Квадратичні ірраціональності (загальний випадок)
- •4.8. Поняття про інтеґрали, які не "беруться"
- •5. Визначений інтеґрал
- •5.1. Задачі, які ведуть до поняття визначеного інтеґрала
- •5 .1.1. Площа криволінійної трапеції
- •5.1.2. Кількість виготовленої продукції
- •5.1.3. Довжина пройденого шляху.
- •5.2. Визначений інтеґрал
- •5.3. Властивості визначеного інтеґрала
- •5.3.1. Лінійність та адитивність
- •5 .3.2. Інтеґрування нерівностей. Теорема про середнє
- •5.4. Визначений інтеґрал як функція своєї верхньої межі
- •5.5. Формула ньютона - лейбніца
- •5.6. Основні методи обчислення визначеного інтеґрала
- •5.6.1. Заміна змінної (спосіб підстановки)
- •5.6.2. Інтеґрування частинами
- •6. Застосування визначеного інтеґрала
- •6.1. Дві схеми застосування визначеного интеґрала
- •6.2. Площі плоских фігур: доповнення
- •6.3. Довжина дуги кривої
- •6.4.1. Об"єм тіла з відомими площами паралельних поперечних перерізів
- •6.4.2. Об"єм тіла обертання
- •6.5. Деякі економічні застосування
- •7. Наближене обчислення визначеного інтеґрала
- •7.1. Формули прямокутників
- •7.2. Формула трапецій
- •7.3. Формула симпсона1 (формула парабол)
- •8. Невласні інтеґрали
- •8.1. Невласні інтеґрали першого роду
- •8.2. Невласні інтеґрали другого роду
- •8.3. Ознаки збіжності невласних інтеґралів
- •8.4. Гама-функція ейлера
- •9. Подвійний інтеґрал
- •9.1. Подвійний інтеґрал та його властивості
- •9.2. Обчислення подвійного інтеґрала в декартових координатах
- •9.3. Невласні подвійні інтеґрали. Формула пуассона
- •9.4. Подвійний інтеґрал в полярних координатах
- •4. Невизначений інтеґрал 206
- •4.2. Невизначений інтеґрал 208
5.3. Властивості визначеного інтеґрала
5.3.1. Лінійність та адитивність
1 (однорідність). Сталий множник k може бути винесений за знак визначеного інтеґрала,
![]() .
.
■Утворимо інтеґральні суми для лівої и правої частин. Вони рівні, оскільки
![]() .
.
Тому їх границі, тобто відповідні визначені інтеґрали, є також рівними.■
2 (адитивність відносно
підінтеґральної
функції).
Якщо
![]()
![]() - дві інтеґровні
функції, то
- дві інтеґровні
функції, то
![]() .
.
Доведіть цю властивість самостійно.
Наслідок (лінійність).
Для будь-яких двох
інтеґровних
функцій
і довільних
сталих
![]()
![]() .
.
3 (адитивність відносно інтервалу інтеґрування). Для будь-яких a, b, c
![]() ,
,
якщо принаймні два з трьох інтеґралів існують.
■1) Нехай спочатку c(a, b). Утворимо інтеґральну суму так, щоб c було точкою ділення. В такому випадку (позначення зрозумілі)
![]() ,
,
і перехід до границі при доводить властивість.
2) Нехай
тепер розташування
точок a,
b, c
довільне,
наприклад,
![]() .
Застосовуючи перший
випадок до
інтервала
.
Застосовуючи перший
випадок до
інтервала
![]() і означення
5, отримаємо
і означення
5, отримаємо
![]()
звідки
![]() .■
.■
5 .3.2. Інтеґрування нерівностей. Теорема про середнє
4. Якщо
a < b
і
підінтеґральна
функція
![]() невід"ємна
на відрізку
,
невід"ємна
на відрізку
,
![]() ,
то
,
то
![]() .
.
Інтеґрал строго додатний, якщо функція неперервна на відрізку і не дорівнює нулю тотожно.
■ Невід"ємність
інтеґрала
безпосередньо
випливає
з додатності інтеґраль-ної
суми для
функції
![]() Його строга
додатність,
як можна довести більш
складними міркуваннями, є
результатом неперервності
функції. ■
Його строга
додатність,
як можна довести більш
складними міркуваннями, є
результатом неперервності
функції. ■
5. Якщо
a < b
і
![]() на
,
то
на
,
то
![]() .
.
Інтеґрали пов"язані строгою нерівністю, якщо функції неперервні на відрізку і не рівні тотожно.
■Достатньо
застосувати
попередню
властивість
до різниці![]() .■
.■
Приклад 2.
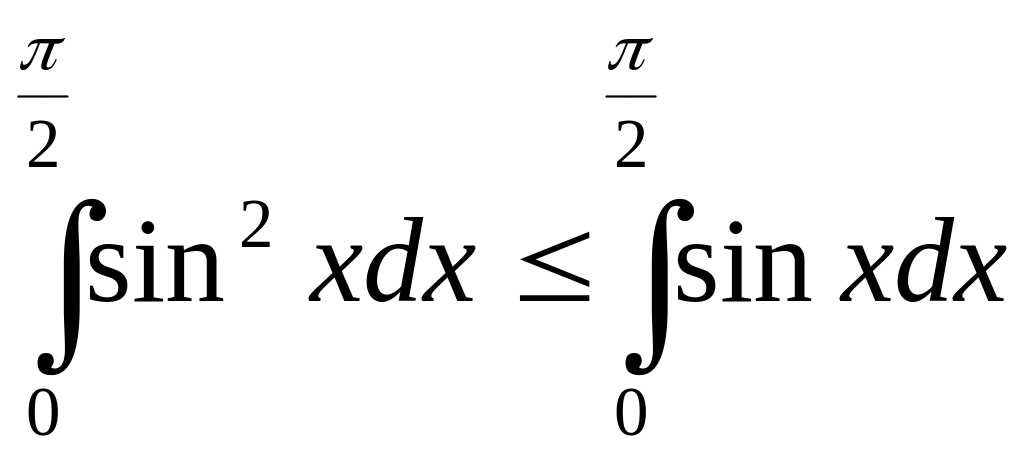 ,
,
оскільки
![]() на відрізку
на відрізку
![]() .
.
6. Якщо a < b, то
![]() ( 17 )
( 17 )
■ Достатньо застосувати властивість 5 до подвійної нерівності
![]() ■
■
7 (двобічна оцінка визначеного інтеґрала). Якщо a < b і функція неперервна на відрізку a, b, то справедливою є подвійна нерівність
![]() .
( 18 )
.
( 18 )
■Доведення випливає
з властивості 5, нерівності
![]() на
та формули
(13).■
на
та формули
(13).■
Приклад 3. Оцінити інтеґрал
![]() .
.
Маємо
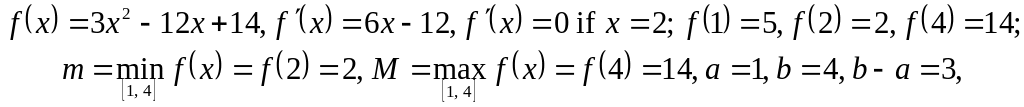
і на підставі формули (18)
![]() .
.
 8.
Теорема про
середнє.
Якщо функція
непнрервна на відрізку
,
то існує точка
8.
Теорема про
середнє.
Якщо функція
непнрервна на відрізку
,
то існує точка
![]() така, що
така, що
![]() ( 19 )
( 19 )
Рис. 3 ■Нехай, наприклад, a < b. Діленням обох частин не-рівності (18) на додатне число отримуємо
![]() .
.
Згідно з теоремою Больцано1–Коші для функції, яка неперервна на відрізку , існує точка така, що
![]() .
.
Випадок
![]() розглядається таким
же чином. Зробіть
це самостійно.■
розглядається таким
же чином. Зробіть
це самостійно.■
Геометричний
сенс
теореми про
середнє
(рис. 3). Площа криволінійної
трапеції
(1) дорівнює
площі
прямокутника
ABCD з
тією ж
основою
AD=a,
b
і висотою
![]() .
.
Означення 6. Вираз
![]() ( 20 )
( 20 )
називається середнім значенням функції на відрізку a, b.
5.4. Визначений інтеґрал як функція своєї верхньої межі
 Нехай
xa,
b.
Розглядемо функцію
Нехай
xa,
b.
Розглядемо функцію
![]() ,
( 21 )
,
( 21 )
тобто
визначений
інтеґрал
с змінною верхньою межею
x.
Геометрично (для невід"ємної підінтеґ-
Рис.
4 ральної
функції
![]() )
цей інтеґрал
дає площу
тієї частини
криволінійної
трапеції
)
цей інтеґрал
дає площу
тієї частини
криволінійної
трапеції
![]() ,
,
яка
лежить між
прямими
![]() (рис. 4).
(рис. 4).
Теорема 2. Якщо функція неперервна на відрезку a, b, то для будь-якого похідна інтеґрала (21) дорівнює
 ,
( 22 )
,
( 22 )
тобто похідна визначеного інтеґрала з змінною верхнью межею x по цій межі дорівнює значенню підінтеґральної функції в точці x.
■За означенням похідної
![]() .
.
Використовуючи адитивність визначеного інтеґрала відносно інтервалу інтеґрування, маємо
![]()
Нехай,
наприклад,
![]() .
На підставі теореми
про середнє
існує така точка
.
На підставі теореми
про середнє
існує така точка
![]() в інтервалі
в інтервалі
![]() ,
що
,
що
![]() .
.
При
цьому
![]() ,
якщо
,
якщо
![]() .
Беручи до уваги неперервність
функції f,
ми дістаємо
.
Беручи до уваги неперервність
функції f,
ми дістаємо
![]() .■
.■
Наслідок (основна теорема інтеґрального числення). Кожна функція, неперервна на відрізку a, b, має первісну на a, b.
■Однією з таких первісних є інтеґрал (21) з змінною верхньою межею x.■
Приклад 4. Знайти похідну функції
![]() .
.
Згідно з формулою (22)
 .
.
Приклад 5. Знайти похідну функції
![]() .
.
Використовуючи властивість адитивності визначеного інтеґрала відносно інтервалу інтеґрування, правило диференціювання складеної функції та формулу (22), отримуємо

![]()
