
- •Дифференциальное исчисление функций одной переменной
- •§1. Производная
- •1. Понятие производной
- •§2. Дифференциал функции
- •1. Понятие дифференциала
- •2. Дифференциал сложной функции
- •3. Таблица формул для дифференциалов
- •§3. Производные высших порядков
- •§4. Возрастание и убывание функций. Максимумы и минимумы.
- •1. Возрастание и убывание функции.
- •2. Максимумы и минимумы функции.
- •§5. Наибольшее и наименьшее значения функции на отрезке
Дифференциальное исчисление функций одной переменной
§1. Производная
1. Понятие производной
Задача о скорости химической реакции.
Пусть дана функция
m=m(t),
где m
- количество некоторого вещества,
вступившего в химическую реакцию к
моменту времени t.
Приращению времени ∆t
будет соответствовать приращение ∆m
величины m.
Отношение
![]() -
средняя скорость химической реакции
за промежуток времени ∆t.
Предел этого отношения при стремлении
∆t
к 0, т.е.
-
средняя скорость химической реакции
за промежуток времени ∆t.
Предел этого отношения при стремлении
∆t
к 0, т.е.
![]() - скорость химической реакции в данный
момент времени t.
Рассмотрим математическую операцию,
требуемую для решения данной задачи:
- скорость химической реакции в данный
момент времени t.
Рассмотрим математическую операцию,
требуемую для решения данной задачи:
Пусть функция f(x) определена в интервале (а;b), возьмем х(а; b). Затем возьмем новое значение аргумента х+∆х из этого промежутка, придав первоначальному значению х приращение ∆х0 (положительное или отрицательное). Этому новому значению аргумента соответствует и новое значение функции у+∆у=f(x+∆х), где ∆у=f(x+∆х)-f(x) – приращение функции.
Составим отношение
∆у
к ∆х:
![]() =
=![]() .
.
Определение1. Если существует предел отношения ∆у к ∆х, когда ∆х→0, то этот предел называется производной от функции у=f(x) в данной точке х и обозначается у или f(x). Таким образом
![]() или
или
![]() .
.
Действие нахождения производной функции называется дифференцированием, а функцию, имеющую производную в точке х, называют дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке промежутка, называется дифференцируемой в этом промежутке.
Пример.
Найдем производную функции у=с (с=const).
Придадим произвольной
точке х приращение ∆х0.
Соответствующее приращение функции:
∆у=с-с=0. Следовательно,
![]() и
и
![]() .
.
![]()
2) Найдем производную функции у = sin х.
![]()
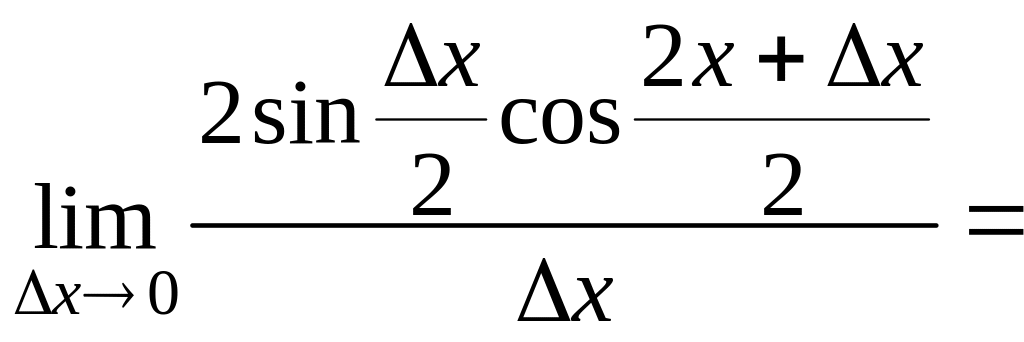

(sinх)=cosх
Замечание. Из рассмотренной выше задачи о скорости химической реакции, получим, что скорость химической реакции есть производная вещества m по времени t, т.е. =m(t).
Теорема (необходимое условие дифференцируемости). Если функция у=f(x)- дифференцируема в некоторой точке х, то она непрерывна в этой точке.
2. Правила дифференцирования и производные элементарных функций
Вывод общих правил дифференцирования.
Пусть даны функции U(x) и V(x), имеющие производные U(x) и V(x)
1) Производная суммы.
Пусть у=U+V, найдем у.
![]()
![]()
![]()

2) Производная произведения
![]()
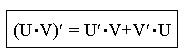
3) Вынесение постоянного множителя за знак производной
![]()
4) Производная частного
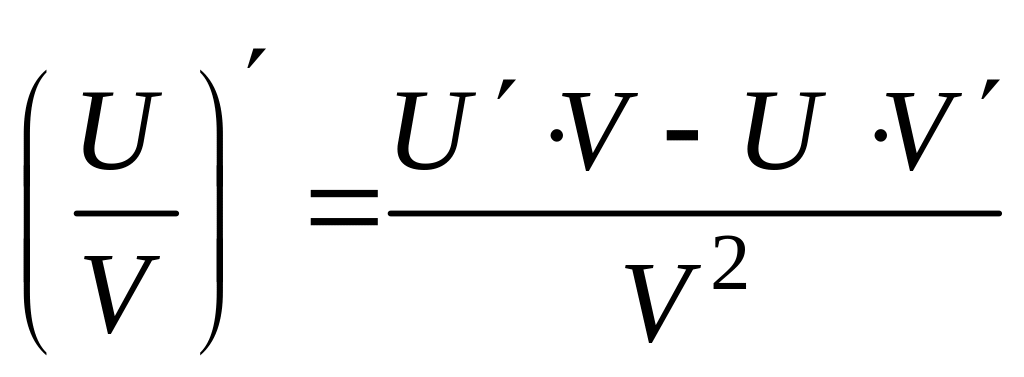
5) Производная сложной функции
Пусть переменная у зависит от переменной U, т.е. у=f(U), а переменная U зависит от переменной х, т.е. U=(x). Функция f(U) имеет производную по переменной U, функция (x) имеет производную по переменной х. Тогда сложная функция y=f((x)) тоже имеет производную по переменной х, которая равна производной внешней функции f(U), умноженной на производную внутренней функции (x):
у(х)= у(U)·U(х)
Пример.
у=sin 3х, у=cos 3х·(3x)=3cos 3x.
6) Производная обратной функции.
Пусть у=f(x)
и х=(у)-
взаимно обратные функции, тогда если
функция у=f(x)
имеет производную у=f(x)0,
то обратная функция имеет производную
(у)
и (у)=![]() или х(у)=
или х(у)=
![]() .
.
Производные тригонометрических функций
1) (sin х)=cos х , (sin U(х)) = U(х)٠cos U(х)
2)
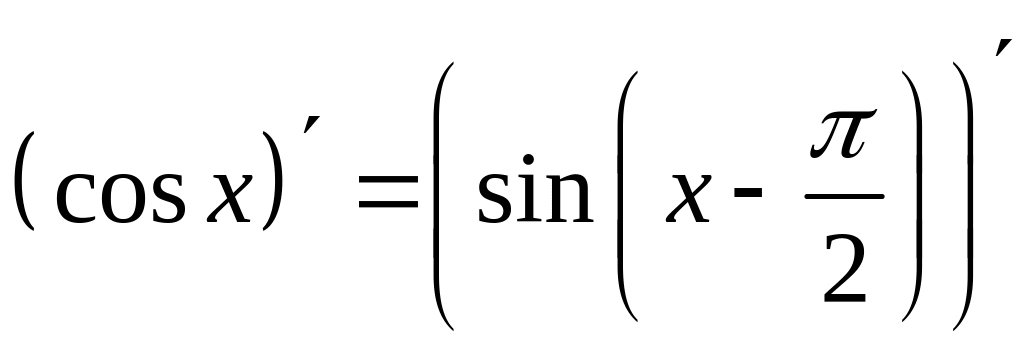

 .
.
(cos U(х)) = - U(х) ٠ sin U(х)
3) (tg
х)
=![]() ,
(tg
U(х))
=
,
(tg
U(х))
=
![]()
4) (сtg
х)
= -
![]() ,
(сtg
U(х))
=
,
(сtg
U(х))
=
![]()
Производная логарифмической функции:
1)(ln
x)
=![]() ,
(ln
U(х))
=
,
(ln
U(х))
=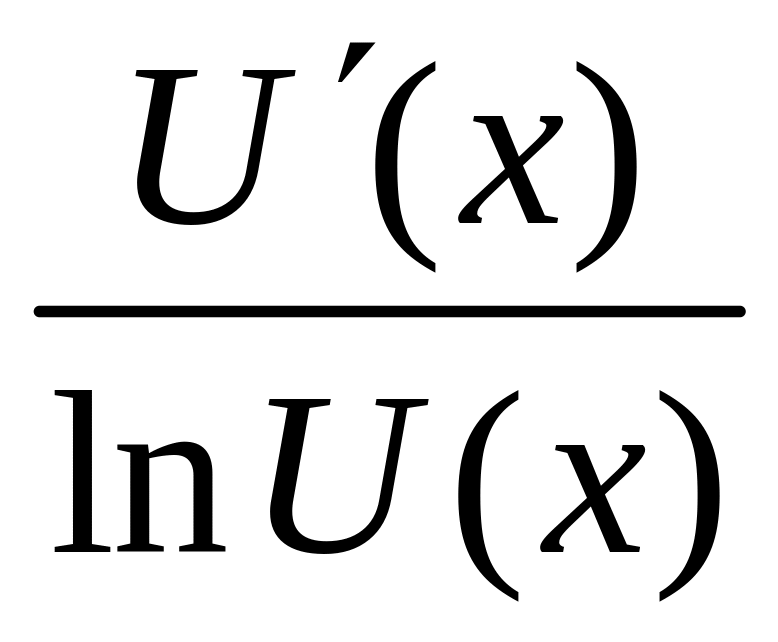
2) (loga
x)=
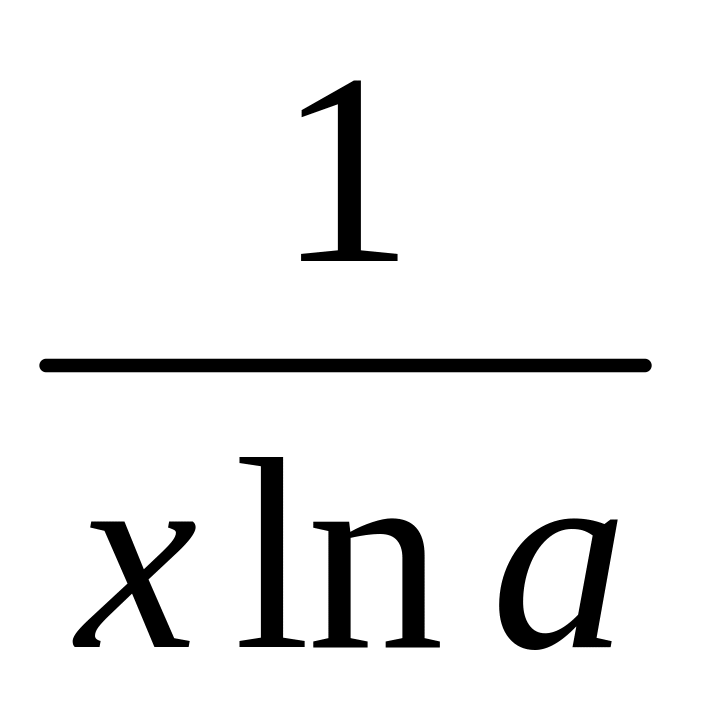 ,
(loga
U
(x))=
,
(loga
U
(x))=
Производная степенной функции:
y = хα , α R, х > 0
(хα) = α · хα-1
((U(х))α) = α ·(U(х))α-1·U(х)
Производная показательной функции:
(ах) = ах · ln а
(ех) = ех
(еU(х)) = еU(х)·U(х)
Производные обратных тригонометрических функций:
Функция у = arcsin х является обратной по отношению к функции х=sin у, тогда
(arcsin
х)=![]() =
=![]() =
=![]() =
=![]() ,
-
,
-![]() y
y
(arcsinx)=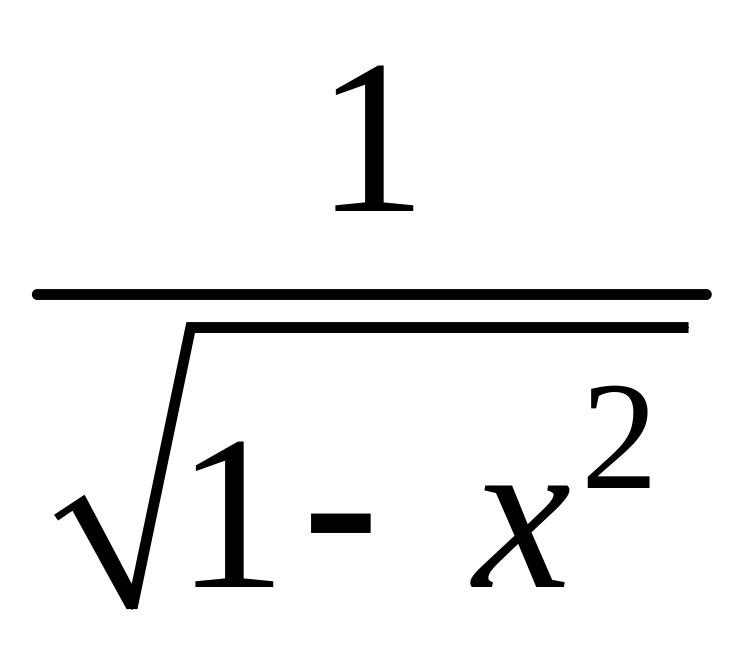
(arcsin
U(х))=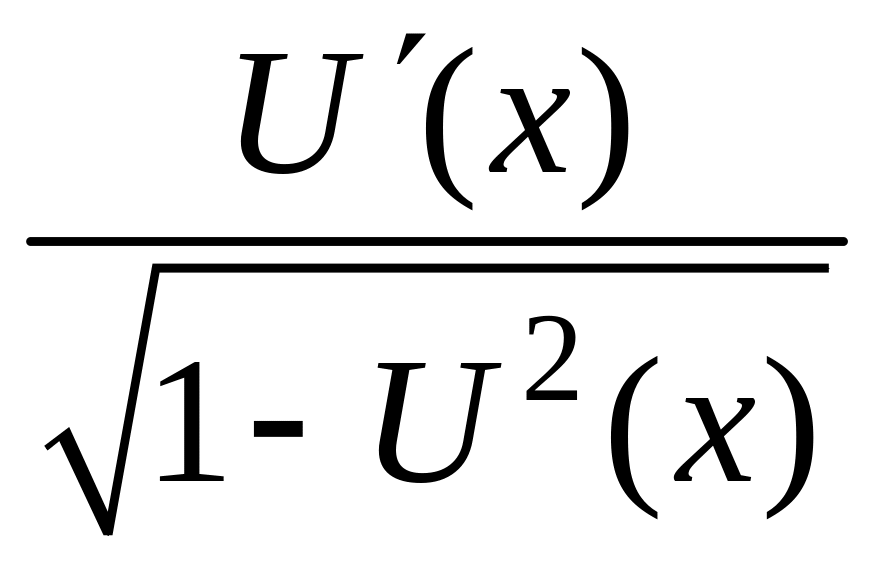
(arccos
х)= ,
0yπ
,
0yπ
(arccos
U(х))=
(arctg x)
=![]() ,
(arctg U(х))=
,
(arctg U(х))=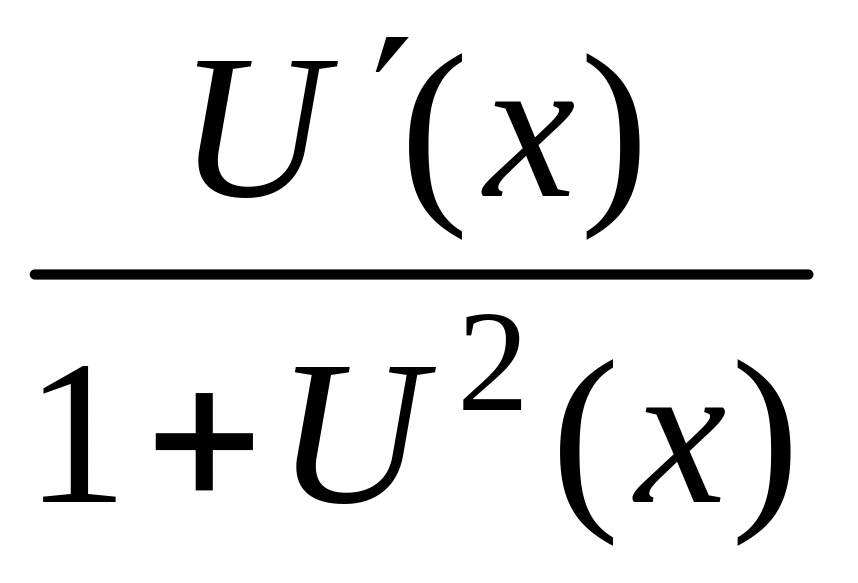
(arcctg
x)=-
,
(arcctg U(х))=

