1. Решение систем нелинейных уравнений

Система нелинейных уравнений с р неизвестными обычно имеет вид

f_i (x₁, .... х_р) = 0, i=1, .... р,

где хотя бы одна функция f_i нелинейная.

Для решения такой системы в редких случаях можно применить метод последовательного исключения неизвест­ных, который приводит решение системы к решению одного нелинейного уравнения с одним неизвестным с последующей подстановкой.

Например, для решения нелинейной системы

x y² +4 = 0,

x - y² +5 = 0

из второго уравнения найдем х = у² — 5 и подставим в первое, получим уравнение с одним неизвестным: у²(у² - 5) + 4 = 0, корни которого

y₁ = 1, у₂ = - 1, y₃ =2, y₄ = -2.

Следовательно, решениями системы являются точки

A (-4, 1), В(- 4, -1), С( -1, 2), D( - 1, -2).

Однако в подавляющем большинстве случаев нели­нейные системы решают итерационными методами.

6.1. Метод простой итерации

Метод простой итерации применим к системам, кото­рые предварительно приведены к виду x₁ = φ₁ (x₁, .... х_р)

…………………………………………. (6.1)

x_p = φ_p (x₁, .... х_р)

или, в векторной форме, х = Ф(х). (6.2)

Пусть x⁽⁰⁾ = (x₁⁽⁰⁾, .... х_р⁽⁰⁾ ) начальное приближение. Последующие приближения в методе простой итерации находятся по формулам

x₁^(m+)1 = φ₁ (x₁^(m), .... х_р^(m) ),

x₁^(m+1) = φ₁ (x₁^(m), .... х_р^(m) _,), (6.3)

……………….….

x₁^(m+1) = φ₁ (x₁^(m), .... х_р^(m) ),

или, в векторной форме, х^(m+1) = Ф(х^(m) . (6.4)

Если последовательность векторов х^(т) = (x₁^(m), .... х_р^(m) )

сходится к вектору x^* = (x₁^*, ..., х_p*), а функции φ_i (x) непрерывны, то вектор х* является решением системы (6.2). Для получения условий сходимости метода итера­ций введем в р-мерном векторном пространстве какую-либо норму (например, кубическую, октаэдрическую или сферическую).

Теорема 3. Пусть для уравнения (6.2) и начального приближения х⁽⁰⁾ выполнены условия:

1) для х', х" из сферы

||х-х⁽⁰⁾|| ≤ δ (6.5)

вектор-функция Ф удовлетворяет условию ||Ф (х')-Ф (х")|| ≤ q ||х'-х"||, (6.6)

где 0 < q < 1;

2) ||Ф (х⁽⁰⁾) – х⁰ || ≤ (1 – q) δ ,

Тогда уравнение (6.2) в сфере (6.5) имеет единствен­ное решение х*, к нему сходится последовательность (6.4) и погрешность метода оценивается неравенством

||х^(m)-х^*|| ≤ ||Ф (х⁽⁰⁾) – х⁰ || . (6.7)

Сходимость метода итераций считается хорошей, если q ≤ 1/2

Приведем достаточное условие, обеспечивающее вы­полнение неравенства (6.6) в кубической норме. Сфера (6.5) в кубической норме является р-мерным кубом с центром в точке x⁽⁰⁾ = (x₁⁽⁰⁾, ..., х⁽_р⁰⁾):

||х-х⁽⁰⁾|| = . (6.8)

Предположим, что в кубе (6.8) функции φ_i ( i = 1, ..., р ) имеют непрерывные частные производные φ_i / x_k, k = 1,... ..., р. Неравенство (6.6) будет выполнено, если φ_i / x_k, удовлетворяют в кубе (6.8) условию

(6.9)

Пример. Методом простой итерации найти реше­ние системы

f₁ (x, y) = 2x – sin 0,5 (x - y) = 0,

f₂ (x, y) = 2y – cos 0,5 (x + y) = 0,

с точностью ε = 10 ^-2.

Решение. Графически отделяем корни системы. Из рис. 5.1 видно, что корень единственный и расположен в квадрате |х| ≤ 0,5, |у — 0,5| ≤ 0,5.

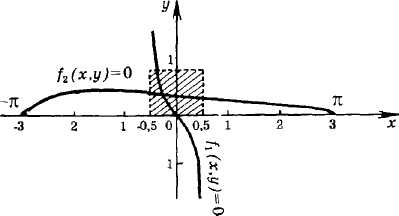
Рис. 6.1

Преобразуем данную систему к виду

х = 0,5 sin 0,5 (х - y) ≡ φ₁ (х, у),

y = 0,5 cos 0,5 (х + y) ≡ φ₂ (х, у).

Убеждаемся, что неравенство (6.9) выполнено q ≤ 0,5. За начальное приближение возьмем х_о = 0, у_о = = 0,5. Дальнейшие вычисления отражены в табл. 6.1.

Таблица 6.1

п	хп yn	0,5 ( xn - yn ) 0.5( уn + хn )	sin 0,5 (хп - уп) cos 0,5 (хп + уп)
0	0 0,5	-0,25 0,25	- 0,234383 0,968913
1	-0,117160 0,48446	-0,30081 0,18365	-0,29659 0,98318
2	-0,148295 0,491592	-0,31994 0,171648	-0,31452 0,98530
3	-0,157246 0,492652	- 0,324949 0,167703	-0,31926 0,98597