Решение нелинейных уравнений с использованием надстройки Подбор параметра.

Корни нелинейного уравнения можно найти, используя надстройку Excel Подбор параметра. Продемонстрируем это для нашего уравнения (5.1).

За нулевое приближение решения уравнения, как это видно из рис.11, можно принять х₀ =2 или х₀ =1,5.

Последовательность действий.

1. Заготовьте таблицу, как показано на рис.11. Введите в ячейку А4 значение нулевого приближения корня, х0=1,5. Значение ячейки В4 будет изменяться в процессе решения (подбора параметра). Первоначально введите туда значение х_0, т.е. 1,5 (B4=1,5).

2. Введите в ячейку С4 формулу левой части уравнения (5.1), т.е. С4=В4*Ln(В4)-1 (смотри строку формул).

Рис. 11.

3. Задайте команду: меню Сервис\Подбор параметра.

4. В появившемся окне, рис.12 , сделайте следующие установки:

• в 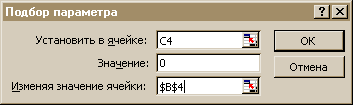поле Установить в ячейке укажите адрес ячейки С4, т.е. формулу левой части уравнения (5.1);

• в поле Значение задайте правую часть уравнения, т.е. 0 (ноль);

• в поле Изменяя значение ячейки укажите ячейку В4, в которой первоначально было занесено нулевое приближение корня х₀ и нажмите кнопку ОК.

Рис.12.

Если все было сделано правильно, то в ячейке В4 будет получено приближенное значение корня нашего уравнения, рис.12.

Повторите расчет для случая х₀ =2.

Сравните полученные результаты с аналогичными, полученными выше.

VI. Реализация методов численного интегрирования с использованием электронных таблиц Microsoft Excel.

Методы численного интегрирования для интеграла (6.1) можно реализовать средствами Excel

(6.1)

Определенный интеграл функции у=f(x) (f(x)>0 или f(x)<0, х[a, b]) пропорционален площади криволинейной трапеции, образованной подынтегральной функцией на отрезке [a, b].

Разобьем отрезок [a, b] на n равных отрезков с шагом . Криволинейная трапеция соответственно разобьется на n элементарных криволинейных трапеций. Площадь каждой элементарной криволинейной трапеции заменяем другой фигурой, площадь которой вычисляется достаточно просто, например прямоугольником (метод прямоугольников) или линейной трапецией (метод трапеций). Сумма площадей этих фигур, называемая интегральной суммой , даст приближенное значение искомого интеграла.

Таким образом, для метода входящих прямоугольников можно записать:

. (6.2)

Аналогичным образом записываются формулы выходящих и средних прямоугольников.

А для метода трапеций интегральная сумма имеет вид:

(6.3)

где

y_i = f(x_i), i=0,1,…,n,

- множество точек (узлов) x_i отрезка [a, b] называемое равномерной сеткой (или просто сеткой):

Вычисления могут сопровождаться значительными погрешностями. Для снижения погрешности следует уменьшить шаг разбивки (метод половинного шага), либо использовать более точные методы.

Метод половинного шага заключается в вычислении двух приближенных значений интеграла (двух итераций) соответственно для двух сеток и , с шагом . Если два соседних приближения близки, т.е. выполняется условие

, (6.4)

тогда за приближенное значение интеграла принимается интегральная сумма с точностью ε, т.е.

Пример 6.1. Используя численные методы вычислить определенный интеграл:

. (6.5)

Последовательность действий

1. Создайте таблицу по образцу рис.13.

2. В ячейку D1 введите количество разбивок n=5. В ячейки В1, В2 и В3 введите значения нижнего и верхнего пределов интегрирования а, b и шаг соответственно. Изменяя в дальнейшем значения этих ячеек, можно вычислить значение интеграла с любой точностью  и для различных пределов интегрирования. Изменение значений этих ячеек должно привести к автоматическому пересчету всей таблицы приложением Excel

3. В столбце А сформируйте номер узла разбивки следующим образом: введите в ячейку А6 ноль, а в ячейку А7 введите формулу =А6+1 и скопируйте ее вниз до конца таблицы, т.е. до n=5.

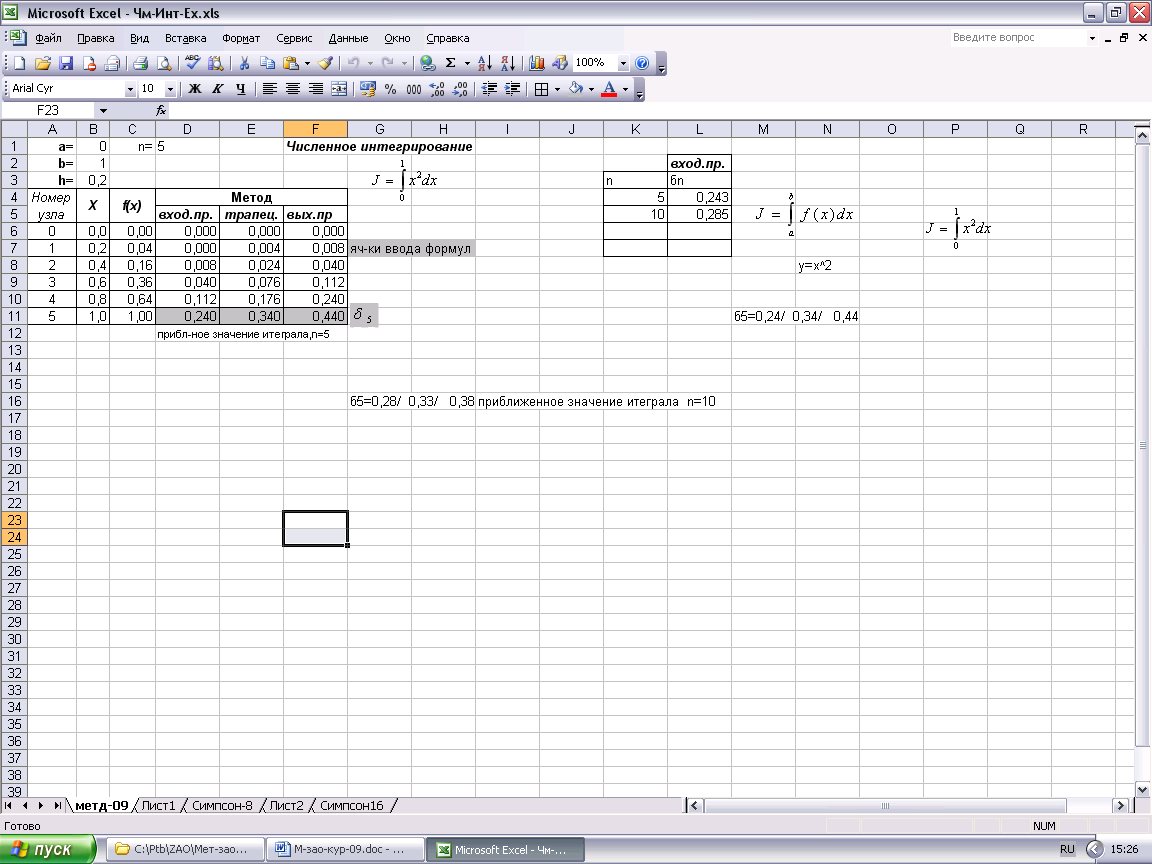
Рис.13

4. В столбце В сформируйте значения узлов равномерной сетки 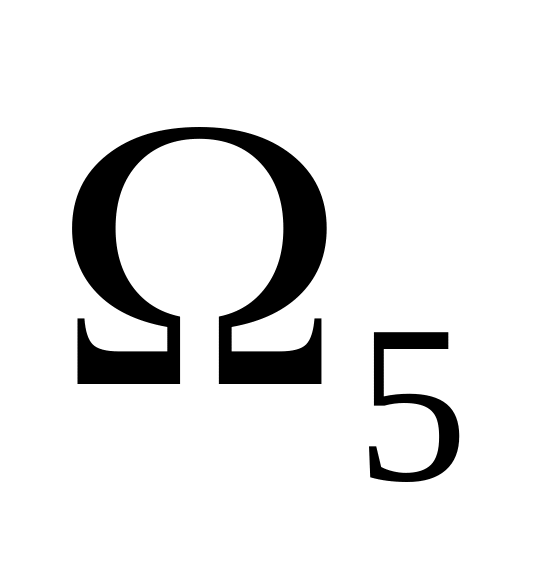, воспользовавшись формулой x_i+1=x_i+h, i=0,1,2,….…Для этого в ячейку В6 введите значение a, т.е. B6=B1. В ячейку В7 запишите формулу B7=B6+$B$3 и скопируйте ее вниз до конца таблицы, т.е. до значения нижнего предела интегрирования b.

5. В столбце С сформируйте значения подынтегральной функции f(x) в узлах сетки. Для этого в ячейку С6 введите формулу С6=В6*В6 и скопируйте ее вниз.

В столбцах D, E и F накапливаются результаты суммирования в соответствии с формулами (6.2), (6.3). Для этого обнулите ячейки D6, E6 и F6. В ячейки D7, E7и F7 запишите формулы численного интегрирования и скопируйте их вниз до конца таблицы:

D7=D6+C6*$B$3

E7=E6+(C6+C7)*$B$3/2

F7=F6+C7*$B$3

Приближенное значение интеграла (6.1) получено в ячейках D11, F11 по методу прямоугольников и в E11 – по методу трапеций соответственно.

В данном случае не составляет труда найти точное значение этого интеграла, используя формулу Ньютона-Лейбница:

и сравнить с полученными результатами.

Изменяя значения ячеек В1 (нижний предел интегрирования а), В3 (шаг h), С6 (формула подынтегральной функции f(x)) вы можете использовать эту таблицу для вычисления любого определенного интеграла с необходимой точностью.

Например. Уменьшите шаг интегрирования, т.е. введите в ячейку D1 величину 10. Выделите последнюю строку таблицы на рис.13 и cкопируйте ее вниз до значения b=1. Вы получили приближенное значение интеграла (интегральную сумму ) с шагом h/2, заметьте, что количество разбивок при этом увеличилось вдвое.

Аналогичным образом можно изменить и другие параметры.