1.Определители и их свойства. Определитель — многочлен от элементов квадратной матрицы (запись чисел в виде квадратной таблицы, в соответствие которой ставится другое число, т.е. «значение» определителя). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца. Свойства:1). Если в определителе есть нулевой столбец, то определитель ревен нулю.2). Если в определителе поменять местами 2 столбца, то определитель изменит знак на противоположный.3). Если в определителе есть 2 одинаковых столбца, то определитель равен нулю.4). Если в определителе элементы какого-либо столбца умножить на любое число, то весь определитель умножится на это число.5). Если в определителе имеются пропорциональные столбцы, то определитель равен нулю.6). Если в определителе столбцы зависимы, то определитель равен нулю.7). Если к какому либо столбцу прибавить любой другой столбец, умноженный на любое число, то определитель не изменится.8). При транспонировании матрицы определитель не изменится.

2.Теорема Лапласа. Разложение определителя по строке. Согласно теореме Лапласа определитель равен сумме произведений всех миноров k-того порядка на их алгебраические дополнения.Δ=∑ (M_k * A_k ) =a₁₁ A₁₁ +a₂₁ A₂₁+…+a_n1 A_n1. Разложение определителя по элементам i-й строке Разложение по i-й строке: где A_ij — алгебраическое дополнение к минору, расположенному в строке с номером i и столбце с номером j. A_ij также называют алгебраическим дополнением к элементу a_ij.

3. Обратная матрица, алгоритм её нахождения. Обратная матрица — такая матрица, которая удовлетворяет равенству: А * A⁻¹ =Е, где Е - единичная матрица. Матрица имеет обратную матрицу только тогда, когда её определитель не равен нулю. Алгоритм нахождения: 1) Δ ≠ 0, находим определитель; 2) а_ij ↔ A_ij подбираем алгебраические дополнения; 3) Строим матрицу из дополнений. 4) Транспонируем матрицу (столбцы записываем как строки); 5) Каждый элемент этой матрицы делим на определитель, получится обратная матрица.

4. Теорема Крамера. Правило Крамера — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы. Из системы уравнений строим матрицу, находим ее определитель. Затем, вместо столбца поочередно подставляем правую часть системы уравнений (получаем матрицу), и находим определители этих матриц. Согласно теореме Крамера: .

5. Построение поля комплексных чисел. Числа вида a+bi , где a и b - вещественные числа, называются комплексными числами. i =(корень из «-1»)

Сложение: (a + bi) + (c + di) = (a + c) + (b + d)i. Вычитание: (a + bi) − (c + di) = (a − c) + (b − d)i. Умножение: Деление: |z| = Корень (a² + b²)

6. Тригонометрическая форма комплексного числа. Формула Муавра. Алгебраическая форма числа z = a + b*i Тригонометрическая форма числа z = |z| * (cos φ + i * sin φ), где φ – аргумент комплексного числа. а = |z| * cos φ b = |z| * sin φ Формула Муавра для комплексных чисел z = |z| * (cos φ + i * sin φ), утверждает, что .

7. Извлечение корней n-ой степени из комплексных чисел. r ( или к) – все числа от 0 до (n-1). Пример: степень = 3 3-1=2, следует: к=0, к=1, к=2.(до двух) Треугольник в круге.

8. Линейные векторные пространства, определение, примеры. Векторным (или линейным) пространством называется множество R, состоящее из векторов, в котором определены операции их сложения и умножения на действительные числа. 1) х + у = у + х (перестановка сложения); 2) (х + у) + z = x + (y + z) (ассоциативность сложения); 3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условию x + 0 = x: для любого вектора x; 4) для любого вектора х существует противоположный ему вектор у такой, что х + у = 0, 5) 1 · х = х, 6) a(bx) = (ab) х (ассоциативность умножения); 7) (a + b) х = aх + bх (распределительное свойство относительно числового множителя); 8) a(х + у) = aх + aу (распределительное свойство относительно векторного множителя). Примеры: Множество всех векторов на прямой со стандартными операциями сложения векторов и их умножения на вещественные числа образует вещественное векторное пространство . Множество всех векторов плоскости образует векторное пространство . Множество всех векторов трехмерного пространства образует векторное пространство . Множество всех строчных матриц размера 1×n образует векторное пространство. Множество всех столбцовых матриц размера n×1 образует векторное пространство. Таким образом, понятие векторного пространства определяется не природой образующих его элементов, а правилами действий над этими элементами, в качестве которых могут выступать реальные векторы, матрицы, функции или иные математические объекты. Свойства л.п.: 1) В каждом линейном пространстве существует только один нулевой элемент. 2) Для каждого элемента существует только один противоположный элемент. 3) Для каждого вектора x, принадлежащему пространству L верно равенство 0*x=0. 4) Длякаждого   R и   L верно  = 5)Если   =  , то  = 0 или   =  6) (-1) *   = -

9. Линейная зависимость системы векторов, основные свойства. Выражение видаλ₁*A₁+λ₂*A₂+...+λ_n*A_n называется линейной комбинацией векторов A1, A2,...,An с коэффициентами λ1, λ2,...,λn. Определение линейной зависимости системы векторов Система векторов A1, A2,...,An называется линейно зависимой, если существует ненулевой набор чисел λ1, λ2,...,λn, при котором линейная комбинация векторов λ1*A1+λ2*A2+...+λn*An равна нулевому вектору, то есть система уравнений: A1x1+A2x2+...+Anxn =Θ имеет ненулевое решение. Набор чисел λ1, λ2,...,λn является ненулевым, если хотя бы одно из чисел λ1, λ2,...,λn отлично от нуля. Определение линейной независимости системы векторов Система векторов A1, A2,...,An называется линейно независимой, если линейная комбинация этих векторов λ1*A1+λ2*A2+...+λn*An равна нулевому вектору только при нулевом наборе чисел λ1, λ2,...,λn, то есть система уравнений: A1x1+A2x2+...+Anxn =Θ имеет единственное нулевое решение. Система векторов называется линейно зависимой, если существуют не все одновременно равные нулю числа λ1, λ2,…, λn, для которых может быть выполнено соотношение .Свойства:1. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы.2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов. 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны. 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны. 6. Любые 4 вектора линейно зависимы. Нахождение: Проверить, является ли линейно зависимой система векторов:

Решение: 1. Составляем систему уравнений. 2. Решаем ее методом Гаусса:

3. Из последних трех строк таблицы записываем разрешенную систему, равносильную исходной системе.

4. Получаем общее решение системы:

5. Задав по своему усмотрению значение свободной переменной x3 =1, получаем частное ненулевое решение X=(-3,2,1).

Ответ: Таким образом, при ненулевом наборе чисел (-3,2,1) линейная комбинация векторов равняется нулевому вектору -3A1+2A2+1A3=Θ. Следовательно, система векторов линейно зависимая.

10. Ранг, базис системы векторов, их свойства. Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля. Ранг матрицы равен наибольшему числу линейно независимых строк (или столбцов) матрицы. Свойства ранга: 1. Ранг матрицы, полученной транспонированием, равен рангу исходной матрицы. 2. Ранг матрицы останется неизменным, если вычеркнуть или приписать нулевую строку (т. е. строку, все элементы которой равны нулю) или нулевой столбец. Базис — множество таких векторов в векторном пространстве, что любой вектор этого пространства можно выразить линейно через векторы из этого множества - базисных векторов. Свойства базиса: Теорема (о базисном миноре): Пусть r = rang A M — базисный минор матрицы A, тогда: базисные строки и базисные столбцы линейно независимы; любая строка (столбец) матрицы A есть линейная комбинация базисных строк (столбцов). Теорема Кронекера - Капелли: система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. В частности: Количество главных переменных системы равно рангу системы. Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.

11. Лемма о замене и ее следствия. (A-λiE) = 0 Φ(x) = λi – x Ax = λix (A-λiE) = 0.

12.Базис и размерность пространства, их свойства. Базисом линейного пространства L  называется такая конечная упорядоченная линейно независимая система векторов, что любой вектор пространства L является линейной комбинацией этих векторов. В отличие от трехмерного пространства векторов, в некоторых линейных пространствах базис не существует. Пусть L -- линейное пространство всех многочленов с веществеными коэффициентами. Покажем, что в этом пространстве базис не существует. Предположим противное. Пусть векторы   образуют в этом пространстве базис. Каждый вектор пространства L  -- это многочлен. Пусть

Из степеней многочленов   выберем наибольшую и обозначим ее буквой m . Возьмем многочлен   . Так как   и векторы  образуют базис, то   , где    -- вещественные числа. Следовательно,   является суммой многочленов степеней меньших, чем   , и поэтому его степень должна быть меньше, чем   . С другой стороны, по определению, многочлен   имеет степень   . Получили противоречие. Значит, предположение о существовании базиса неверно.         

13.Координаты векторов в базисе, связь между ними при замене базиса.

Пусть в n-мерном линейном пространстве L выбран базис , который мы будем для удобства называть "старый" и другой базис , который мы будем называть "новый". Возьмем призвольный вектор “a” из L . Его координатный столбец в старом базисе обозначим

, а в новом - 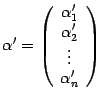. Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно "связать" друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису 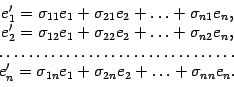Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса Эта матрица называется матрицей перехода от старого базиса к новому. Замечание 18.1 Матрица перехода всегда невырождена, то есть . Предложение 18.5 Координатные столбцы в старом базисе и в новом базисе связаны формулой где справа стоит произведение матрицы перехода на матрицу-столбец. Доказательство. Так как - координатный столбец вектора в новом базисе, то

Заменив векторы их разложениями по старому базису, получим Изменим порядок суммирования

Здесь мы получили разложение вектора по старому базису, причем координата вектора с номером равна . Элемент с номером столбца будет иметь такой же вид. Следовательно, формула доказана.

14. Подпространства, линейная оболочка системы векторов, прямая сумма подпространств. Подпространство - множество P' элементов пространства Р, которое само является пространством в том же смысле, что и пространство Р. Например, всякое множество элементов метрического пространства есть метрическое пространство. В трёхмерном векторном пространстве R3 любая прямая или плоскость являются соответственно пространством. R1 и R2 пространства R3. В частности, пространство, состоящее из одного элемента {θ}, является подпространством любого пространства; любое пространство является само себе подпространством. Подпространства, не совпадающие с этими двумя, называют собственными или нетривиальными. Линейная оболочка L (x) подмножества X линейного пространства L — пересечение всех подпространств L, содержащих X. Линейная оболочка является подпространством L. Линейная оболочка также называется подпространством, порожденным X. Говорят также, что линейная оболочка L (x) натянута на множество X. Линейная оболочка L (x) состоит из всевозможных линейных комбинаций различных конечных подсистем элементов из X. В частности, если X — конечное множество, то L (x) состоит из всех линейных комбинаций элементов X. Если X — линейно независимое множество, то оно является базисом L (x) и тем самым определяет его размерность. Понятие прямой суммы распространяется на случай, когда изначально не являются подпространствами какого-либо одного объемлющего линейного пространства. Определим X как декартово произведение и определим в нём операции линейного пространства с помощью формул

Тогда X является линейным пространством, содержащим подпространства Согласно построению, каждый вектор однозначно представим в виде следовательно,

15. Ранг матрицы, его связь с порядками миноров, алгоритм нахождения ранга матрицы методом окаймления миноров. Минор k-го порядка матрицы называется её базисным минором, если он не равен нулю, а все миноры матрицы порядка (k+1) и выше, если они существуют, равны нулю. Ранг матрицы – это порядок её базисного минора. Метод окаймляющих миноров: Метод окаймляющих миноров: Смотри в тетради на странице с точкой.

16. Алгоритм нахождения ранга матрицы методом Гаусса. Смотри в тетради на странице с двумя точками.

17. Общее решение систем линейных уравнений методом Гаусса. В тетради

18. Общее решение систем линейных уравнений путем нахождения базисного минора. В тетради

19. Евклидовы пространства, задание скалярного произведения с помощью матрицы Гаусса. Евклидово пространство — пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3. Обычно n - мерное евклидово пространство как Rⁿ. Действительное линейное пространство E называется евклидовым, если каждой паре векторов сопоставляется число так, что и выполняются аксиомы:

I.

II.

III.

IV.

Число называют скалярным произведением векторов x и y, - скалярным квадратом вектора (пишут ). Введенная операция называется скалярным умножением векторов x и y.

20. Процесс ортогонализации Грама - Шмидта. Ортонормированный базис. Процесс Грама (англ.) ― Шмидта ― наиболее известный алгоритм ортогонализации, при котором по линейно независимой системе строится ортогональная система такая, что каждый вектор bi линейно выражается через , то есть матрица перехода от {ai} к {bi} ― верхнетреугольная матрица. При этом можно добиться того, чтобы система {bi} была ортонормированной и чтобы диагональные элементы матрицы перехода были положительны; этими условиями система {bi} и матрица перехода определяются однозначно. Верхнетреугольная матрица — квадратная матрица, в которой все элементы ниже главной диагонали равны нулю. Базис конечномерного евклидова пространства называется ортонормированным базисом, если образующие его векторы попарно ортогональны и имеют единичную длину.

21. Ортогональное дополнение подпространства, ортогональные проекции и ортогональные составляющие векторов. Ортогональное дополнения подпространства. Пусть в E задано некоторое подпространство E1. Рассмотрим множество E2ЄE элементов x, ортогональных всем элементам из E1. В евклидовом пространстве E совокупность элементов таких, что для называется ортогональным дополнением множества E1. Теорема Ортогональное дополнение k - мерного подпространства является подпространством размерности . Пусть в Eⁿ со стандартным скалярным произведением дан ортонормированный базис и пусть E2 ортогональное дополнение к E1 . Выберем некоторый базис в E1 . Тогда из условия ортогональности произвольного элемента xЄE2 каждому элементу E1 следует (см. теорему 7.4.1.), что или же, в координатной форме,

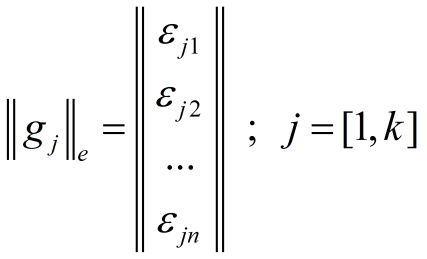, где и .

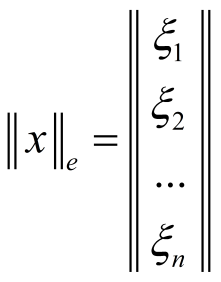Эта однородная система линейных уравнений (неизвестные в которой есть компоненты элемента x), определяющая ортогональное дополнение E2 , имеет ранг k в силу линейной независимости элементов . Тогда, по теореме 6.7.1., у нее есть линейно независимых решений, образующих базис подпространства E2. Теорема доказана. Теорема Если E2 ортогональное дополнение подпространства E1ЄE, то E1 является ортогональным дополнением E2 . Доказательство:

Для каждого элемента xЄE2 по условию следствия имеет место равенство . Но это означает, что для каждого yЄE1 справедливо , то есть E1 является ортогональным дополнением к E2 в E . Теорема доказана. Ортогональная проекция - частный случай параллельной проекции, когда ось или плоскость проекций перпендикулярна (ортогональна) направлению проектирования.

22. Линейные операторы векторных пространств, матрицы операторов. В тетради (лекции) с точкой Линейный оператор - действие, сопоставляющее каждому вектору из Хn единственный вектор из Ym. Матрица оператора в данном базисе – матрица, составленная из коэффициентов разложения образов базисных векторов по базису, записанных по столбцам.

23. Ядро, образ, дефект и ранг линейного оператора. Ядро линейного оператора - множество векторов «х» из пространства «Хn», которые оператором «А» переводятся в нулевой вектор «Уm». Обозначается как ker A. 1. Ядро линейного оператора - подпространство. 2. Размерность ядра равна n-r, где r - ранг оператора. Образ линейного оператора - множество векторов Ах, в которое отображаются всевозможные вектора пространства Хn. (т.е. образ — это область значений оператора). Дефект линейного оператора - называется размерность его ядра. Дефект оператора обозначается как def. (def A= dim ker A) Ранг линейного оператора - размерность его образа. Ранг оператора будем обозначать Rg = dim Img .

24. Собственные векторы и собственные значения линейного оператора, алгоритм их нахождения. Диагонализируемые операторы. (Ненулевой вектор из одномерного подпространства, инвариантного относительно , называется собственным вектором оператора . Таким образом, собственный вектор оператора удовлетворяет условию . При этом скаляр называется собственным значением оператора .) Собственные значения и собственные векторы линейного оператора Пусть A - линейный оператор, действующий в линейном пространстве. Число λ - называется собственным значением, а ненулевой вектор x соответствующим собственным вектором линейного оператора A, если они связаны между собой соотношением Ax = λx . Пусть A - матрица оператора в некотором базисе. Собственные значения оператора и соответствующие им собственные векторы связаны соотношением (A - λE) x = 0, где E - единичная матрица, а 0 - нулевой элемент пространства x. Это означает, что собственный вектор оператора является ненулевым решением линейной однородной системы (A - λE) x = 0, которое существует тогда и только тогда, когда det(A - λE) x = 0. Следовательно, собственные значения линейного оператора могут быть вычислены как корни уравнения det(A - λE) x = 0, а собственные векторы -- как решения соответствующих однородных систем. Уравнение det(A - λE) x = 0 называется характеристическим уравнением оператора, а многочлен det(A - λE) x - характеристическим многочленом оператора. Для собственных значений и собственных векторов линейного оператора справедливы следующие утверждения: характеристический многочлен оператора, действующего в n-мерном линейном пространстве является многочленом n-й степени относительно λ; линейный оператор, действующий в n-мерном линейном пространстве имеет не более n различных собственных значений; собственные векторы, отвечающие различным собственным значениям, линейно независимы; если линейный оператор, действующий в n-мерном линейном пространстве X, имеет n различных собственных значений, то собственные векторы оператора образуют базис в пространстве X; этот базис называют собственным базисом оператора; матрица оператора в базисе из его собственных векторов имеет диагональную форму с собственными значениями на диагонали. Алгоритм нахождения: Составим характеристическое уравнение

или

Раскроем скобки и приведём подобные слагаемые

Отсюда

или Вынесем общий множитель за скобки. Тогда получим уравнение Произведение равно нулю, когда один из сомножителей равен нулю. Получаем совокупность уравнений Второе уравнение совокупности - квадратное уравнение с отрицательным дискриминантом Следовательно оно не имеет действительных корней. Поэтому характеристическое уравнение имеет только один действительный корень , а матрица только одно собственное значение . Найдём собственный вектор, принадлежащий этому собственному значению, решая уравнение Расписывая по компонентам и подставляя , получим систему из трёх уравнений с тремя неизвестными:

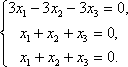Второе и третье уравнения одинаковые. Поэтому систему можно переписать в виде: Сложим оба уранения, а затем из второго вычтем первое. Получим Отсюда

и мы имеем, что собственный вектор x= . Диагонализируемые операторы. Def. Оператор называется диагонализируемым, если существует базис, в котором матрица этого оператора диагональна. Примеры: 1) операторы проектирования диагонализируемы, 2) нильпотентные операторы не диагонализируемы (если они не нулевые). Лемма. Пусть характеристический многочлен имеет различных корней, тогда оператор диагонализируемый. Доказательство. Пусть - корни , т.е. собственные значения оператора , а - отвечающие им собственные вектора, т.е. . Значит, если - базис, то матрица оператора в этом базисе имеет вид: 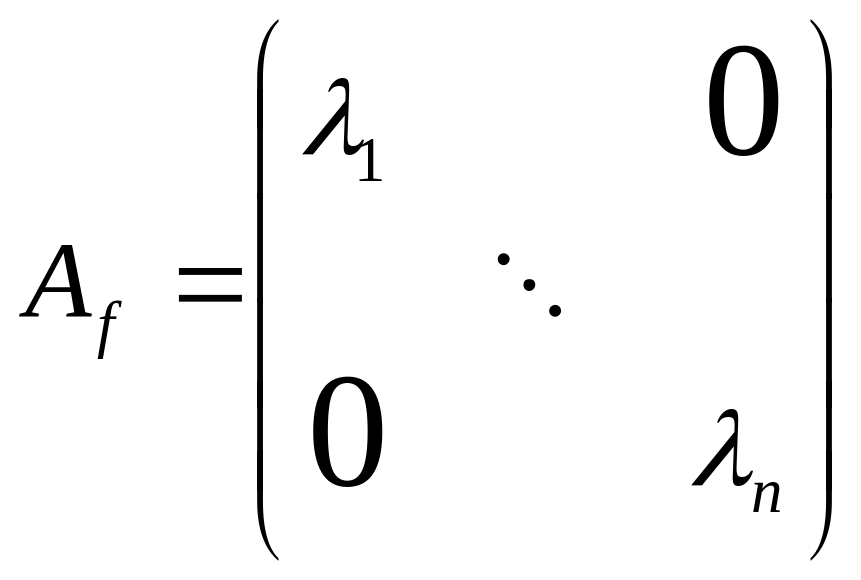. Докажем, что является базисом, для этого нам достаточно доказать линейную независимость этих векторов. Т. dim R³ = dim L₁ + dim L₂ + dim L₃, это значит, что Аφ.

25. Симметричные операторы. Канонический вид и канонический базис симметричного оператора. Оператор φ симметричный если для любых двух векторов эти скалярные произведения верны: ( φ(x) , y ) = ( x , φ(y) ) Для того чтобы линейный оператор был симметричен, необходимо и достаточно, чтобы его матрица в ортонормированном базисе была симметрична. Каноническим видом формы является такой вид, в котором нет произведений переменных. Канонический вид симметричного оператора –

26. Ортогональные операторы и матрицы. Канонический вид и канонический базис ортогонального оператора. Оператор называется ортогональным, если он сохраняет скалярное произведение, т.е. (Ax, Ay) = (x,y). Ортогональная матрица — квадратная матрица A с вещественными элементами, результат умножения которой на AT равен единичной матрице: AAT = ATA = E, или, что эквивалентно, её обратная матрица равна транспонированной матрице: A^-T = A^T Канонический вид ортогонального оператора В тетради (лекции)на странице с 3 точками. Там же и теорема с определением базиса.

27. Квадратичные формулы, их матрицы, преобразование формы при преобразовании переменных. Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора. Гугл в помощь…

28. Канонический вид квадратичной формы, закон инерции. Метод Лагранжа приведения формы к каноническому виду. Квадратичная форма называется канонической, если все т. е. Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующий способ: Метод Лагранжа - последовательное выделение полных квадратов. Например, если

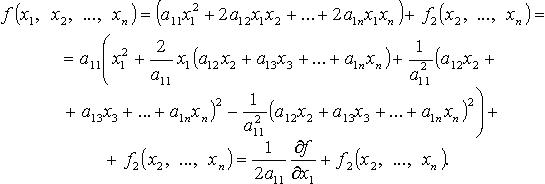Затем подобную процедуру проделывают с квадратичной формой и т. д. Если в квадратичной форме все но есть то после предварительного преобразования дело сводится к рассмотренной процедуре. Так, если, например, то полагаем . Закон инерции квадратичных форм. Приводя квадратичную форму к сумме квадратов: вообще говоря, будем получать различные коэффициенты при квадратах. Однако, справедлива следующая теорема, которая носит название "закон инерции квадратичных форм". Теорема. Если квадратичная форма приводится к сумме квадратов в двух различных базисах, то число членов с положительными коэффициентами и число членов с отрицательными коэффициентами в обоих случаях одни и те же.