
- •Алгебра
- •График учебного процесса
- •III семестр
- •IV семестр
- •1. Цели и задачи дисциплины, место в учебном процессе, требования к уровню содержания дисциплины.
- •2. Технологическая карта дисциплины
- •3. Содержание дисциплины
- •Самостоятельная работа (темы , выносимые на срс и методическая поддержка срс)
- •Литература для самостоятельной работы
- •4. Организация текущего и промежуточного контроля знаний
- •5. Методические рекомендации преподавателю
- •6. Работа с ресурсами Internet
- •7. Материальное обеспечение дисциплины
- •8. Методическое обеспечение дисциплины:
- •Глоссарий
- •Вопросы, выносимые на экзамены
- •III семестр
- •IV семестр
- •Методические рекомендации по организации внеаудиторной и аудиторной самостоятельной работы студентов
- •Контрольно - измерительные материалы
- •III семестр Модуль 1
- •Модуль 2 Контрольная работа по теме «Многочлены от одной переменной»
- •IV семестр Модуль 1 Тест по теме «Многочлены над полем рациональных чисел» для межсессионного учета знаний
- •Контрольная работа по теме «Многочлены над полями рациональных, действительных и комплексных чисел»
- •Модуль 2 Контрольная работа по теме «Расширения полей и задачи, связанные с этим»
- •Методические указания по подготовке практических занятий
- •Методические рекомендации по выполнению курсовых работ
- •Темы курсовых работ
- •1. Вопросы делимости и решения уравнений в кольце целых чисел.
- •. Программа итоговой государственной аттестации студентов
- •Группы и подгруппы
- •Группа подстановок
- •Подгруппы
- •Циклические группы
- •Разложение группы по подгруппе
- •6. Задачи и упражнения для самостоятельного выполнения
- •Нормальные делители. Фактор - группы.
- •1. Нормальные делители
- •2. Фактор – группы
- •Гомоморфизмы групп
- •Задачи и упражнения для самостоятельного выполнения
- •Элементарные сведения о кольцах
- •Кольцо с единицей
- •Делители нуля. Область целостности
- •Поле частных
- •Задачи и упражнения для самостоятельного выполнения
- •Гомоморфизмы колец
- •Понятие идеала. Примеры
- •Операции над идеалами
- •Сравнения и классы вычетов по идеалу. Фактор – кольцо
- •Гомоморфизм колец. Теорема о гомоморфизмах
- •Характеристика кольца с единицей
- •Задачи и упражнения для самостоятельного выполнения
- •Делимость в области целостности
- •2. Кольцо главных идеалов
- •Евклидовы кольца.
- •Задачи и упражнения для самостоятельного выполнения
- •1. Многочлены над полем
- •2. Кольцо многочленов как евклидово кольцо
- •3. Техника деления с остатком. Схема Горнера
- •4. Теорема Безу
- •5. Наибольший общий делитель. Алгоритм Евклида
- •6.Наименьшее общее кратное
- •7. Неприводимые многочлены
- •8. Каноническое разложение многочлена
- •9. Вопросы и упражнения для самостоятельной работы
- •Комплексных чисел
- •1. Вводные замечания
- •2. Свойства модуля многочлена
- •3. Основная теорема алгебры комплексных чисел
- •4. Разложение многочлена над полем с в произведение линейных множителей
- •5. Разложение многочленов над полем r в произведение неприводимых множителей
- •6 Задачи и упражнения для самостоятельного выполнения
- •IV семестр
- •Приводимость и неприводимость многочленов над полем действительных, комплексных и рациональных чисел
- •Рациональные корни многочлена с рациональными коэффициентами
- •Понятие алгебраического числа
- •1. Вводные замечания
- •2. Свойства модуля многочлена
- •3. Основная теорема алгебры комплексных чисел
- •4. Разложение многочлена над полем с
- •5. Разложение многочленов над полем r
- •6 Задачи и упражнения для самостоятельного выполнения
- •1. Алгебраические числа.
- •2. Простое алгебраическое расширение поля.
- •3. Уничтожение иррациональности в знаменателе.
- •4. Конечные расширения полей.
- •6. Вопросы и упражнения для самостоятельной работы.
- •Лекции 7-8
- •Поле алгебраических чисел
- •Понятие разрешимости в квадратных радикалах
- •Определение 1. Алгебраическое уравнение
- •Связь с расширением числовых полей
- •4. Признаки того, что число выражается в квадратных радикалах.
- •5. Общий критерий разрешимости в квадратных радикалах
- •6. Примеры геометрических задач, сводящихся к уравнениям, неразрешимым в квадратных радикалах
- •Задача об удвоении куба
- •Задача о трисекции угла
- •Задача о квадратуре круга
- •7. Вопросы и упражнения для самостоятельной работы
6. Примеры геометрических задач, сводящихся к уравнениям, неразрешимым в квадратных радикалах
Поставим вопрос о возможности того или иного геометрического построения с помощью циркуля и линейки. Такой вопрос относится скорее к алгебре многочленов, нежели к геометрии. Впервые это понял, наверное, Гаусс. В 1801 году в работе «Арифметические исследования» он установил связь между построением правильного
n –
угольника и решением уравнения
![]() в поле комплексных чисел. Он показал,
что если
в поле комплексных чисел. Он показал,
что если
![]() ,
то n-угольник построить
можно.
,
то n-угольник построить
можно.
Например, можно с помощью циркуля и линейки построить правильный
5-угольник, так
как![]() ;
;
17-угольник, так
как![]() .
.
В геометрии
показывается, что корни уравнения
![]() с рациональными коэффициентами могут
быть построены с помощью циркуля и
линейки тогда и только тогда, когда это
уравнение разрешимо в радикалах, то
есть когда решение этого уравнения
сводится к решению цепочки квадратных
уравнений. Покажем, как доказывается
неразрешимость некоторых классических
задач на построение циркулем и линейкой.
с рациональными коэффициентами могут
быть построены с помощью циркуля и
линейки тогда и только тогда, когда это
уравнение разрешимо в радикалах, то
есть когда решение этого уравнения
сводится к решению цепочки квадратных
уравнений. Покажем, как доказывается
неразрешимость некоторых классических
задач на построение циркулем и линейкой.
Задача об удвоении куба
Построить куб, объем которого вдвое больше объема данного куба. Для того, чтобы трактовать эту задачу как задачу на построение на плоскости, нужно понимать её так: на плоскости дан отрезок, равный ребру искомого куба. Итак, пусть дан отрезок – ребро данного куба. Примем этот отрезок за единицу измерения.
Тогда объем
данного куба равен
![]() .
.
Объем искомого
куба равен 2, значит ребро искомого куба
равно
.
Но число
является корнем уравнения
![]() .
.
Значит, длина x ребра искомого куба удовлетворяет условию:
(6).
Но это уравнение имеет
корни:
![]() - комплексные.
- комплексные.
То есть, это уравнение не имеет рациональных корней. А, значит, оно неразрешимо в квадратных радикалах. А это значит, что корни уравнения (6) не могут быть построены с помощью циркуля и линейки.
Задача о трисекции угла
Разделить данный
угол на три равные части.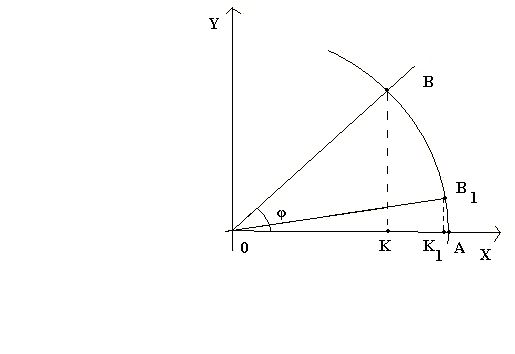 Очевидно, что существуют углы, которые
можно разделить на три равные части с
помощью циркуля и линейки, например
прямой угол. Но эту задачу надо понимать
так: требуется указать алгоритм трисекции
угла с помощью циркуля и линейки,
применимый к любому углу. Пусть угол
АОВ равен φ – мера угла в радианах, а
угол АОВ – произвольный угол. Проведем
окружность произвольного радиуса с
центром в точке О. Выберем систему
координат с центр в точке О и осью ОХ,
совпадающий с прямой ОА. Пусть ОА –
единичный отрезок, тогда точка А имеет
координаты (1,0). Пусть
точка К – проекция точки В на ось ОХ,
тогда К имеет координаты (cos
φ, 0). Пусть теперь точка В1 – такова, что
угол АОВ1 = 1/3 угла АОВ, то есть равен φ/3,
а К1- проекция точки В1 на ось ОХ. И задача
о трисекции угла может пониматься как
задача построения точки В1 по точкам А,
О, К, так чтобы точка В1 имела координаты
(cos φ,0).
Очевидно, что существуют углы, которые
можно разделить на три равные части с
помощью циркуля и линейки, например
прямой угол. Но эту задачу надо понимать
так: требуется указать алгоритм трисекции
угла с помощью циркуля и линейки,
применимый к любому углу. Пусть угол
АОВ равен φ – мера угла в радианах, а
угол АОВ – произвольный угол. Проведем
окружность произвольного радиуса с
центром в точке О. Выберем систему
координат с центр в точке О и осью ОХ,
совпадающий с прямой ОА. Пусть ОА –
единичный отрезок, тогда точка А имеет
координаты (1,0). Пусть
точка К – проекция точки В на ось ОХ,
тогда К имеет координаты (cos
φ, 0). Пусть теперь точка В1 – такова, что
угол АОВ1 = 1/3 угла АОВ, то есть равен φ/3,
а К1- проекция точки В1 на ось ОХ. И задача
о трисекции угла может пониматься как
задача построения точки В1 по точкам А,
О, К, так чтобы точка В1 имела координаты
(cos φ,0).
Найдем
(cos
φ/3 + ί sin φ/3)![]() = cos φ + ί sin
φ (по формуле Муавра)
= cos φ + ί sin
φ (по формуле Муавра)
С другой стороны
(cos
φ/3 + ί sin φ/3)
= cos
φ/3
+ 3 ί cos![]() φ/3
sin φ/3 - 3 cos
φ/3 sin
φ/3-
– ί sin
φ/3 = cos φ/3 ( cos
φ/3
- 3 sin
φ/3)
+ ί sin φ/3 ( 3cos
φ/3
- -sin
φ/3)
φ/3
sin φ/3 - 3 cos
φ/3 sin
φ/3-
– ί sin
φ/3 = cos φ/3 ( cos
φ/3
- 3 sin
φ/3)
+ ί sin φ/3 ( 3cos
φ/3
- -sin
φ/3)
А значит:
cos φ = cos φ/3 - 3 cos φ/3 sin φ/3 = cos φ/3 ( cos φ/3 - 3 sin φ/3).
Откуда:
4 cos φ/3 - 3 cos φ/3 - cos φ = 0
А значит cos φ/3 является корнем уравнения
![]() (7)
(7)
При φ = π/2 получаем
![]() ;
;
![]() уравнение разрешимо в квадратных
радикалах.
уравнение разрешимо в квадратных
радикалах.
Если же φ = π/3 то
![]() = cos π/3 = 1/2 и получаем
уравнение
= cos π/3 = 1/2 и получаем
уравнение
![]() 1/2 = 0 или
1/2 = 0 или
![]() 1
= 0
1
= 0
Положим в нем y
= 2x, получим
![]() - оно не имеет рациональных корней.
Значит, неразрешимо в квадратных
радикалах.
- оно не имеет рациональных корней.
Значит, неразрешимо в квадратных
радикалах.
А значит корни невозможно построить с помощью циркуля и линейки. Значит угол π/3 невозможно разделить на три равные части циркулем и линейкой.
