1 и 2кр. вариант 7

Задание 1

Даны четыре вектора , , и в некотором базисе. Показать, что векторы ,, образуют базис, найти координаты вектора в этом базисе.

7. (3, 4, -3); (-5, 5, 0); (2, 1, -4); (8, -10, 17).

Решение:

Положим что ,, образуют базис

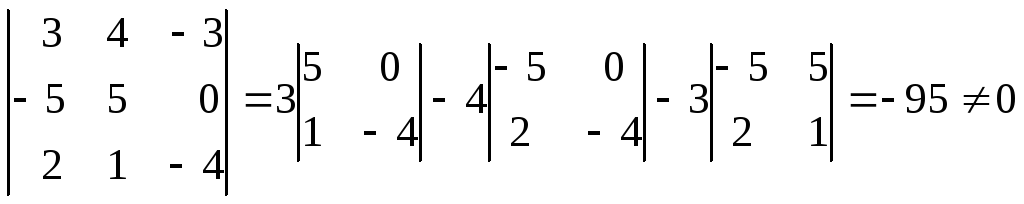
Значит вектора образуют базис

Найдем координаты в новом базисе по правилу Крамера:

=-3-5

Задание 2

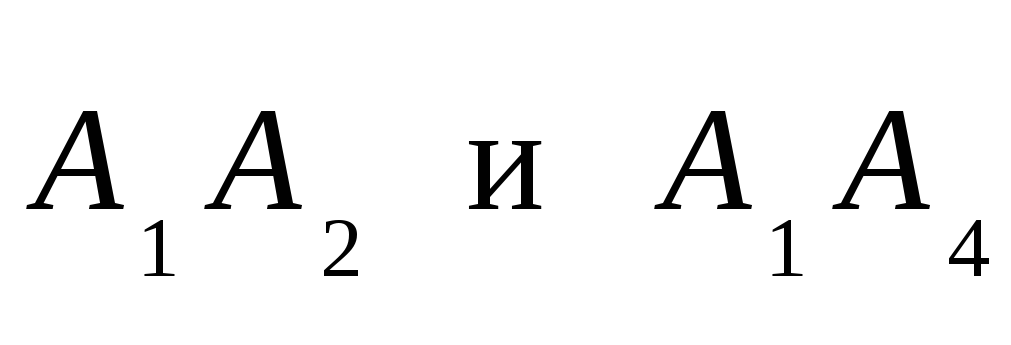Даны координаты вершин пирамиды . Найти:1) длину ребра ; 2) угол между ребрами ; 3) угол между ребром и гранью ; 4) площадь грани ; 5) объем пирамиды; 6) уравнения прямой; 7) уравнение плоскости ; 8) уравнение высоты, опущенной из вершины на грань . Сделать чертеж.

17.

Решение:

=(3-5;8-5;4-4)=(-2;3;0)

=(3-5;5-5;0-4)=(-2;0;6)

=(5-5;8-5;2-4)=(0;3;-2)

1) Длина ребра

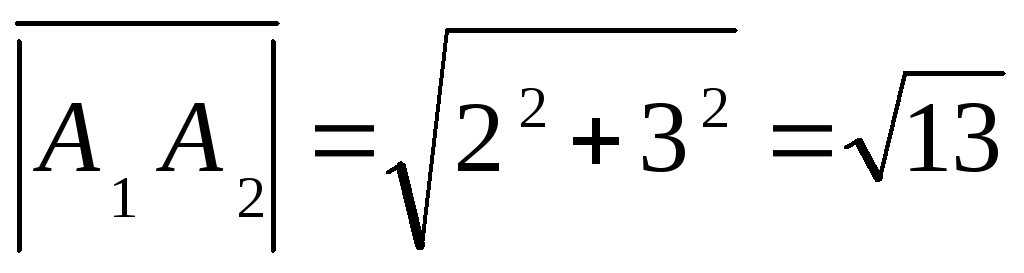
2) Угол φ

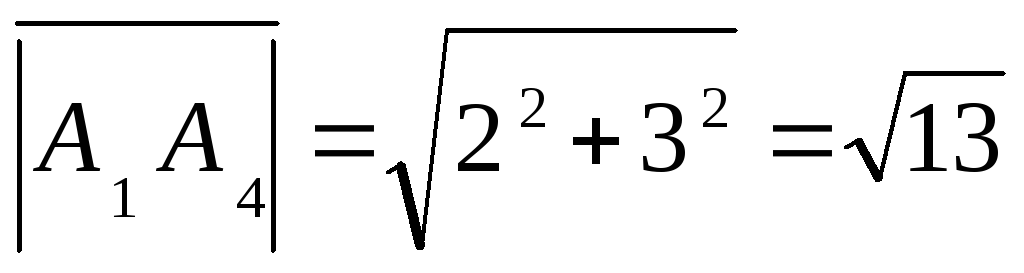
3) Угол между ребром и гранью ; 4) площадь грани

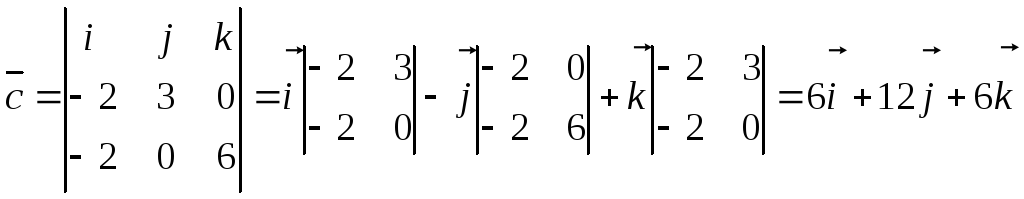
4) Площадь грани

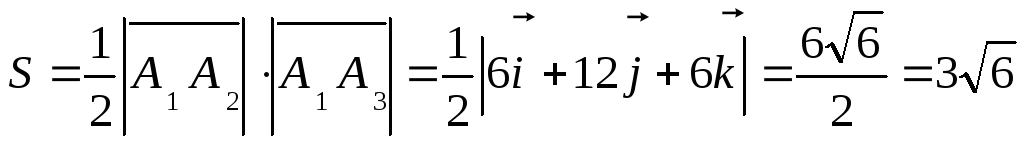
5) Объем пирамиды

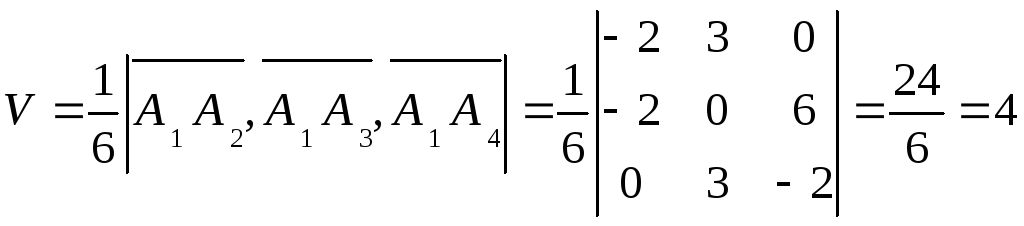
6) Уравнения прямой

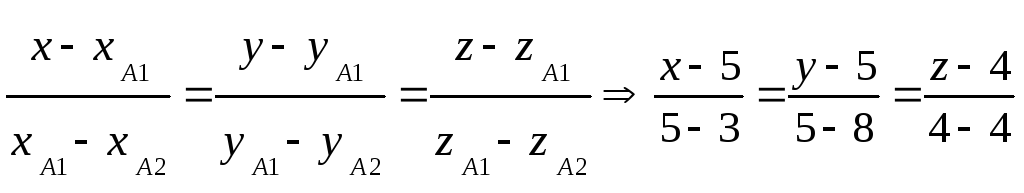
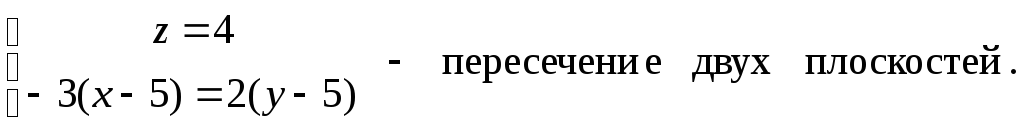
7) Уравнение плоскости

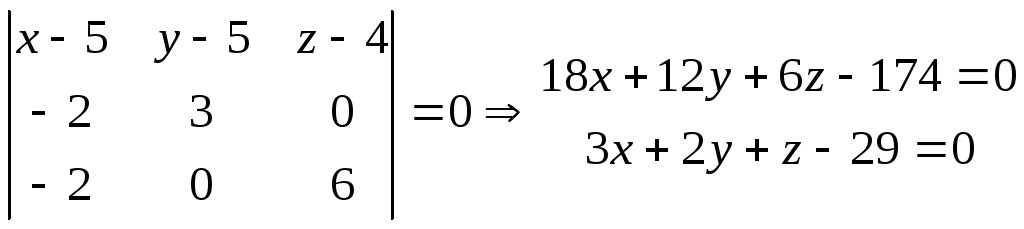
8) Уравнение высоты, опущенной из вершины на грань

вектор нормальный к плоскости (3;2;1)

- каноническое уравнение.

9) Чертеж

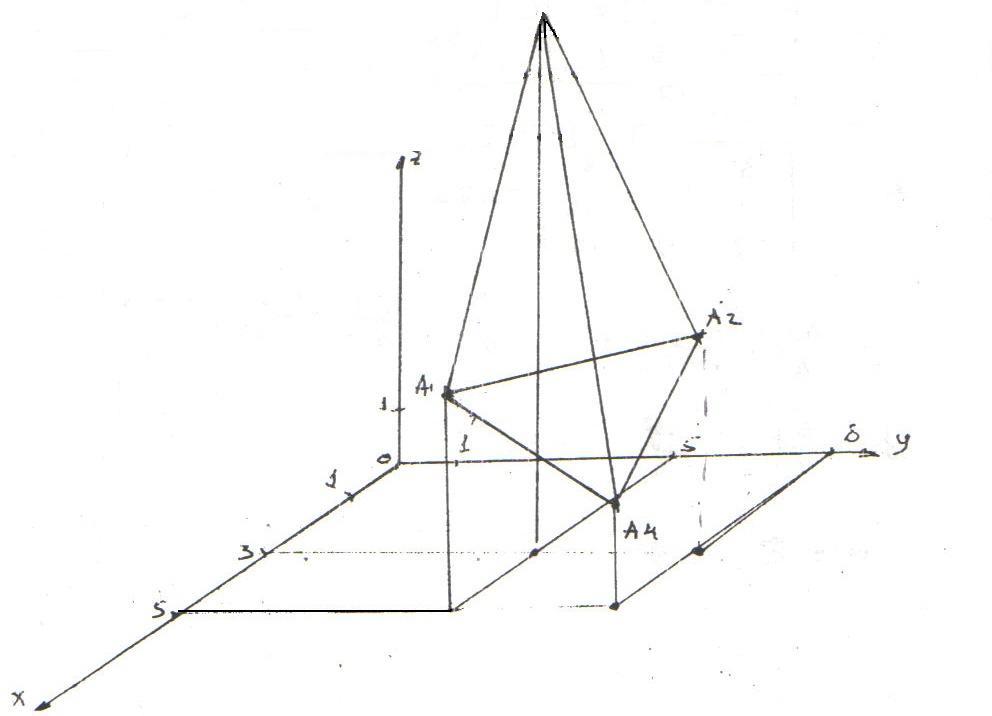
Задание 3

27. Составить уравнение линии, для каждой точки которой расстояние от точки А(0,1) вдвое меньше расстояния от прямой у=4.

Решение:

А(0,1), y=4

По условию

MB=2MA

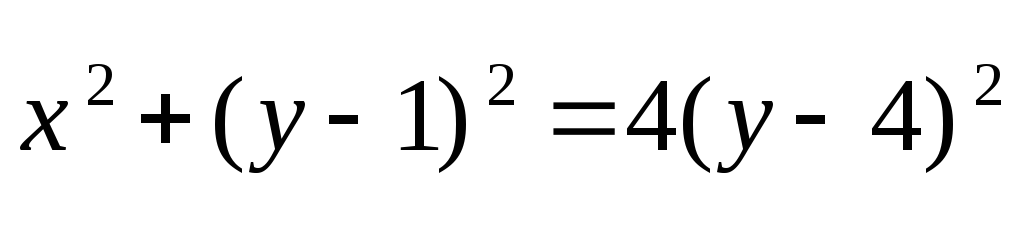
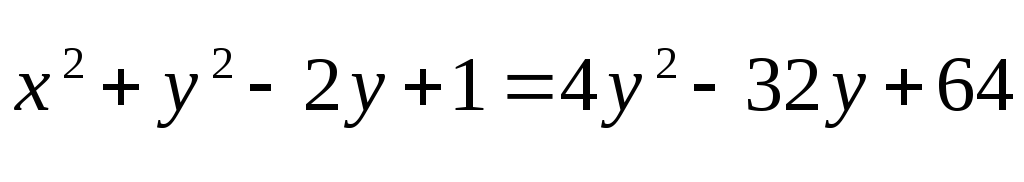
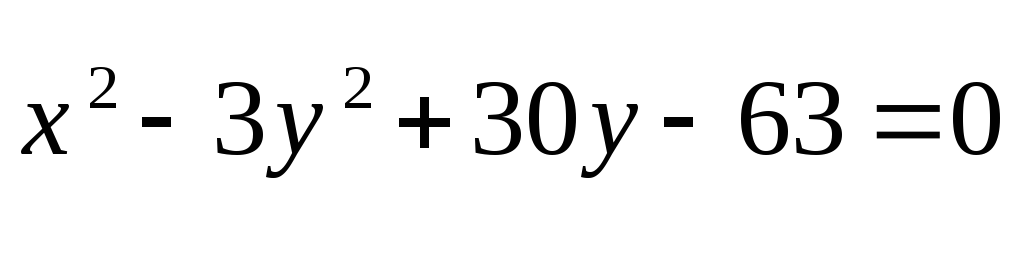
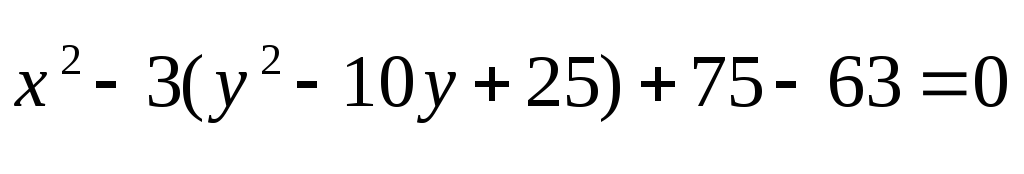
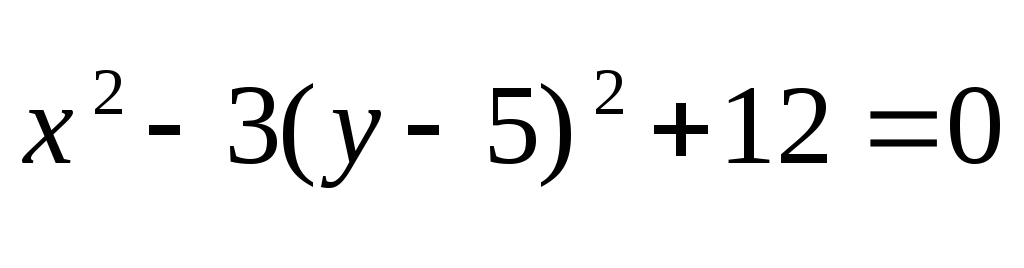
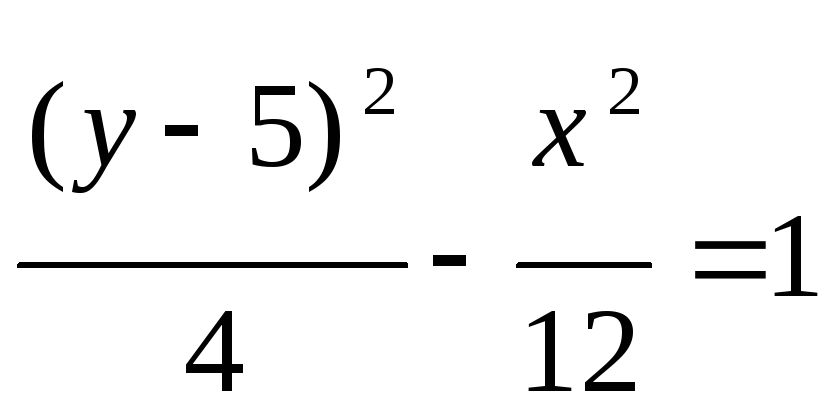- гипербола с большими полуосями:

Ответ:

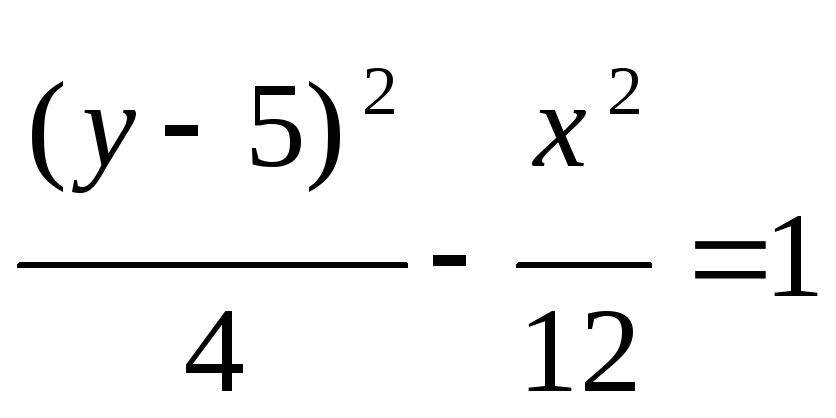
Задание 4

Доказать совместимость данной системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления:

Решение:

1) Рассмотрим расширенную матрицу

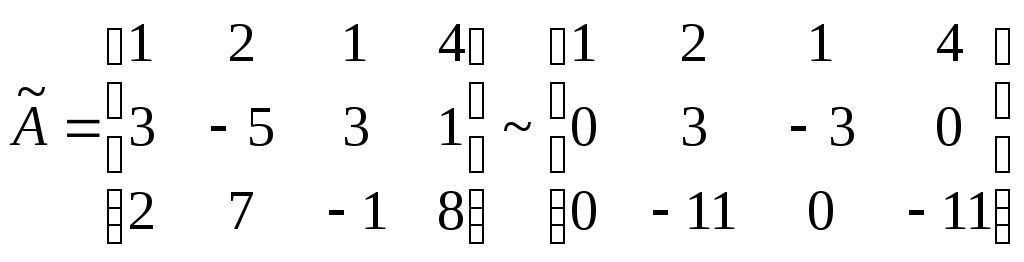
Ранг основной матрицы и расширенной равны 3. система имеет единственное решение:

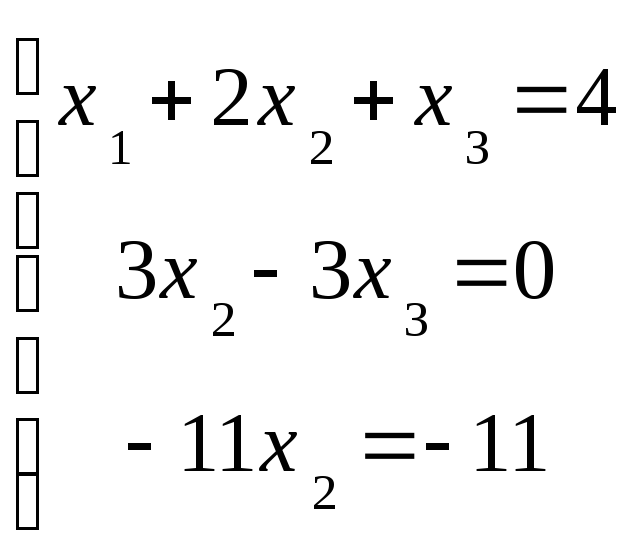
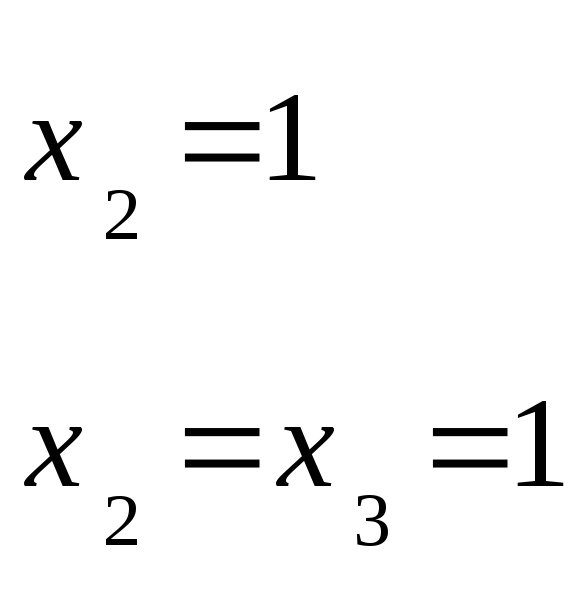
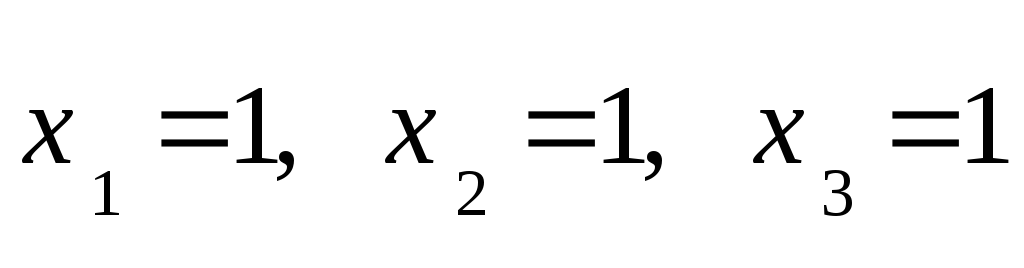
2) средствами матричного исчисления:

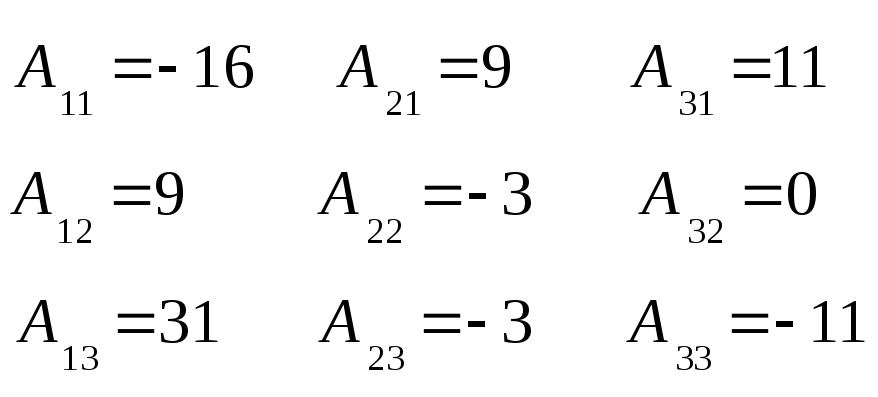
Задание 5

Найти размерность и базис пространства решений однородной системы линейных уравнений:

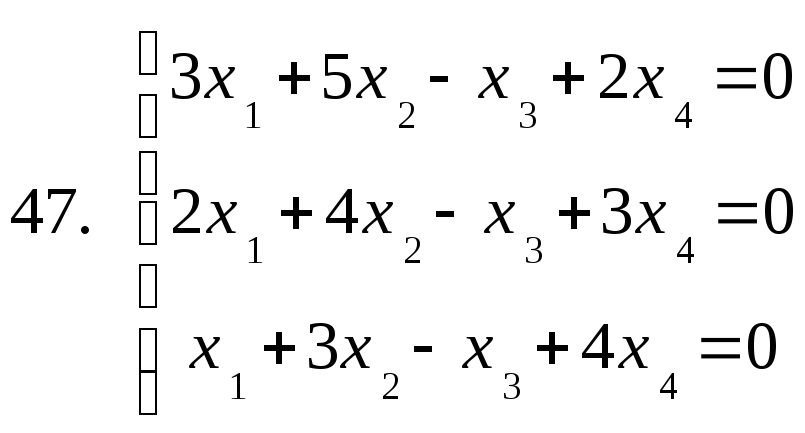
Решение:

Так как ранг системы меньше числа неизвестных, то система имеет ненулевые решения. Размерность пространства решений этой системы n - r =2

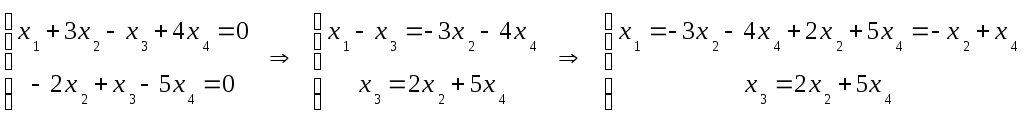
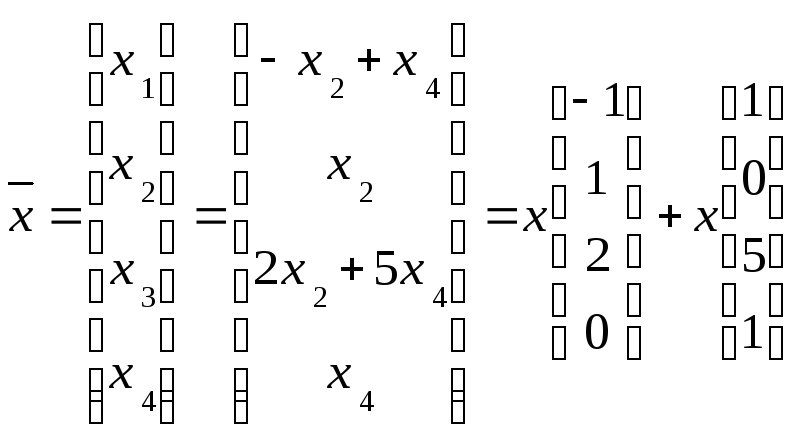
Базис пространства решений данной системы

Задание 6

Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей:

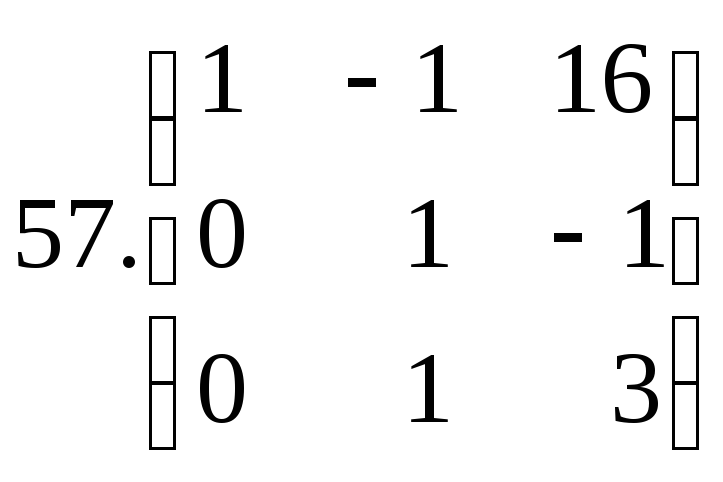
Решение:

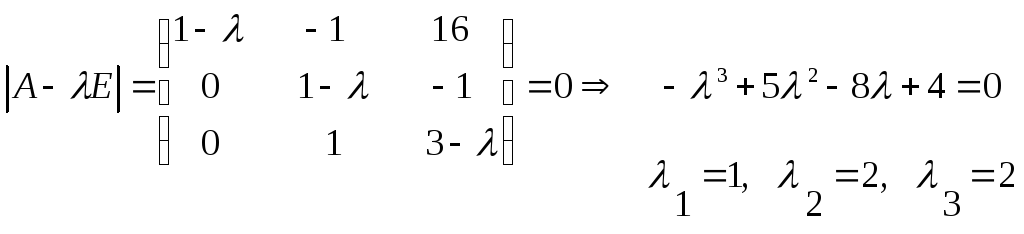
Находим собственные векторы:

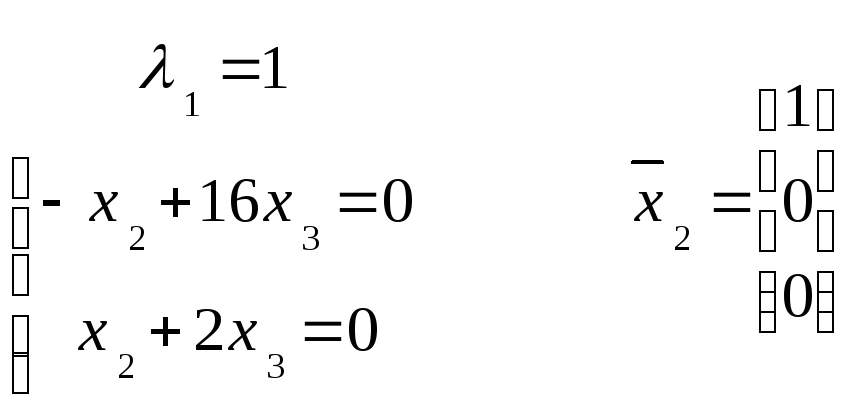
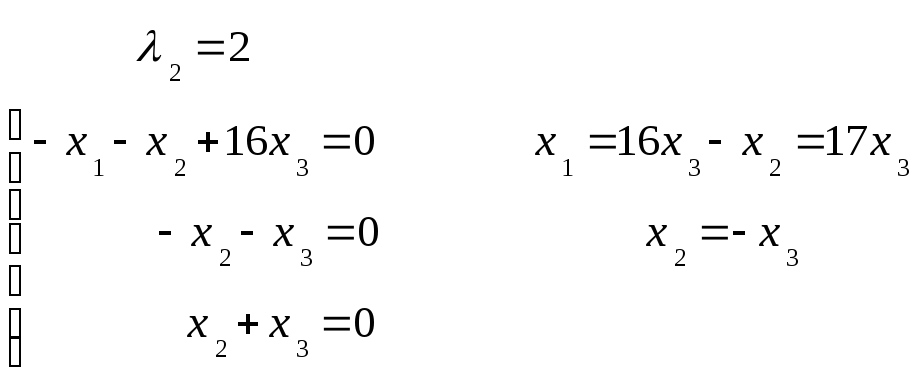
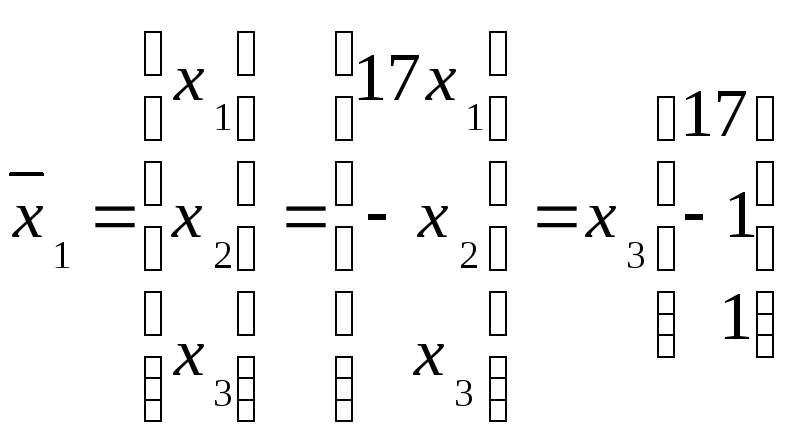
Собственные значения

Собственный вектор

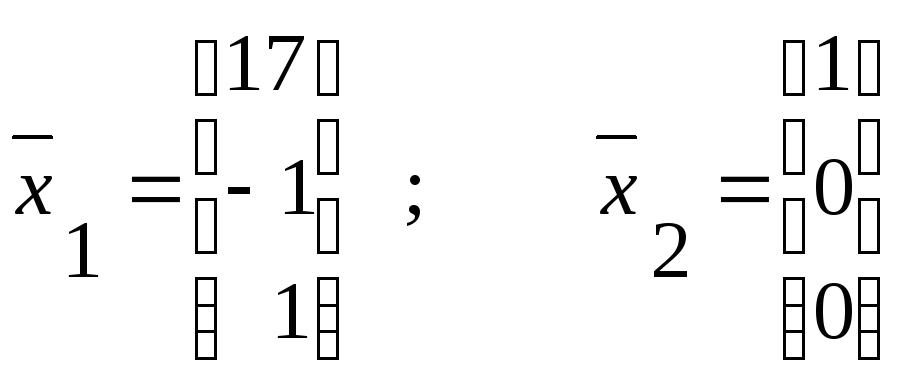
Задание 7

Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм:

67.

Решение:

Квадратичная форма с матрицей А=

Рассмотрим характеристическое уравнение:

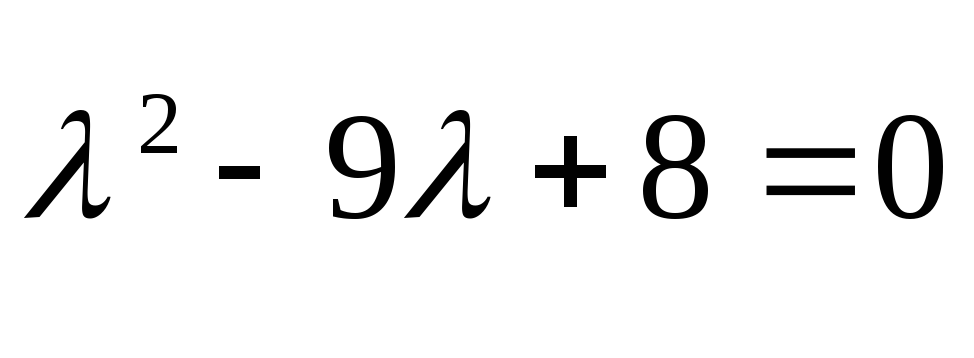
Находим собственные вектора:

Номеруем собственные вектора:

Матрица перехода от старого базиса к новому:

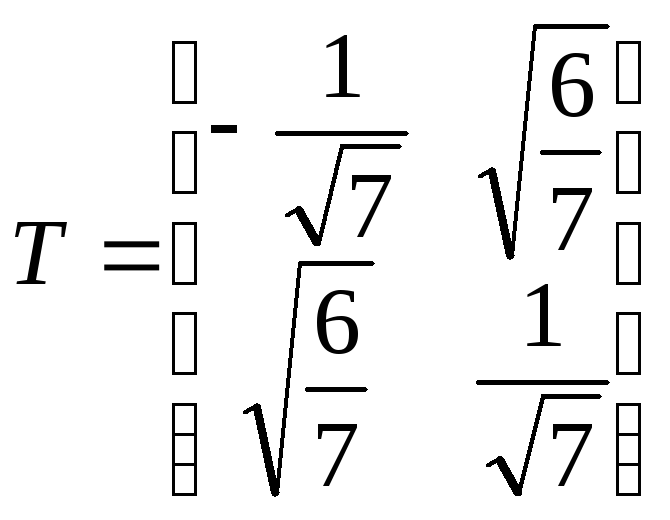
Выполняем преобразование:

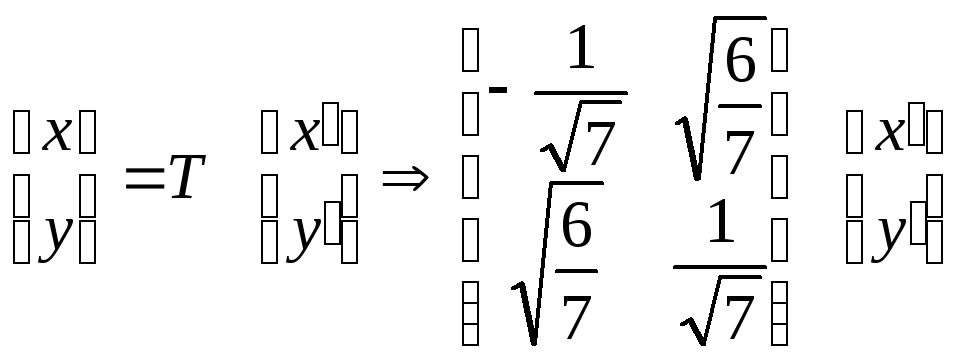
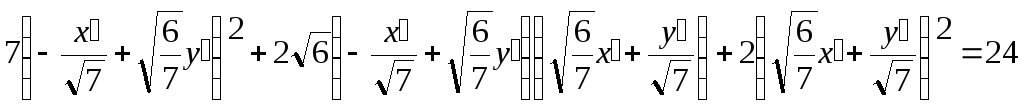
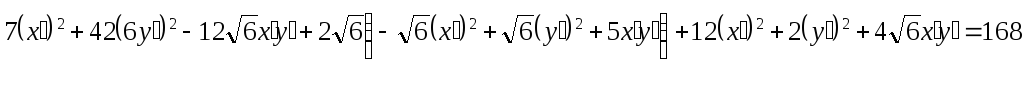
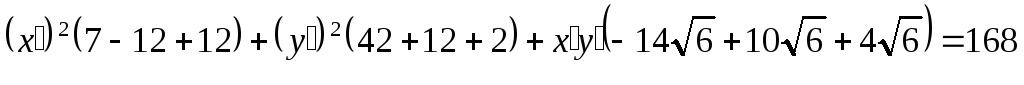
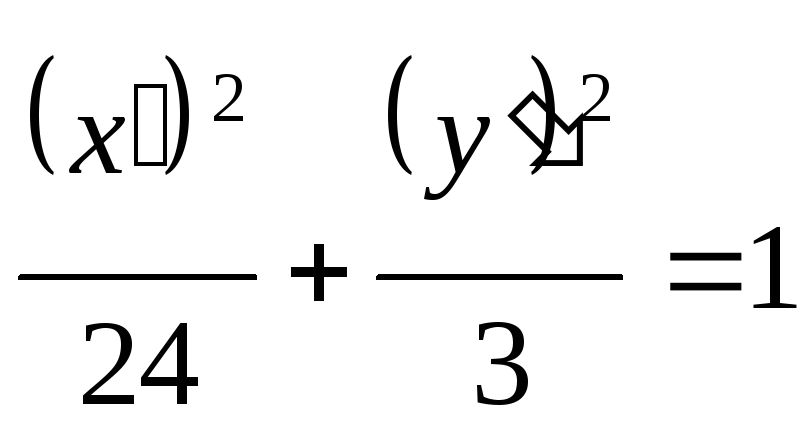- эллипс с большими полуосями

Задание 8

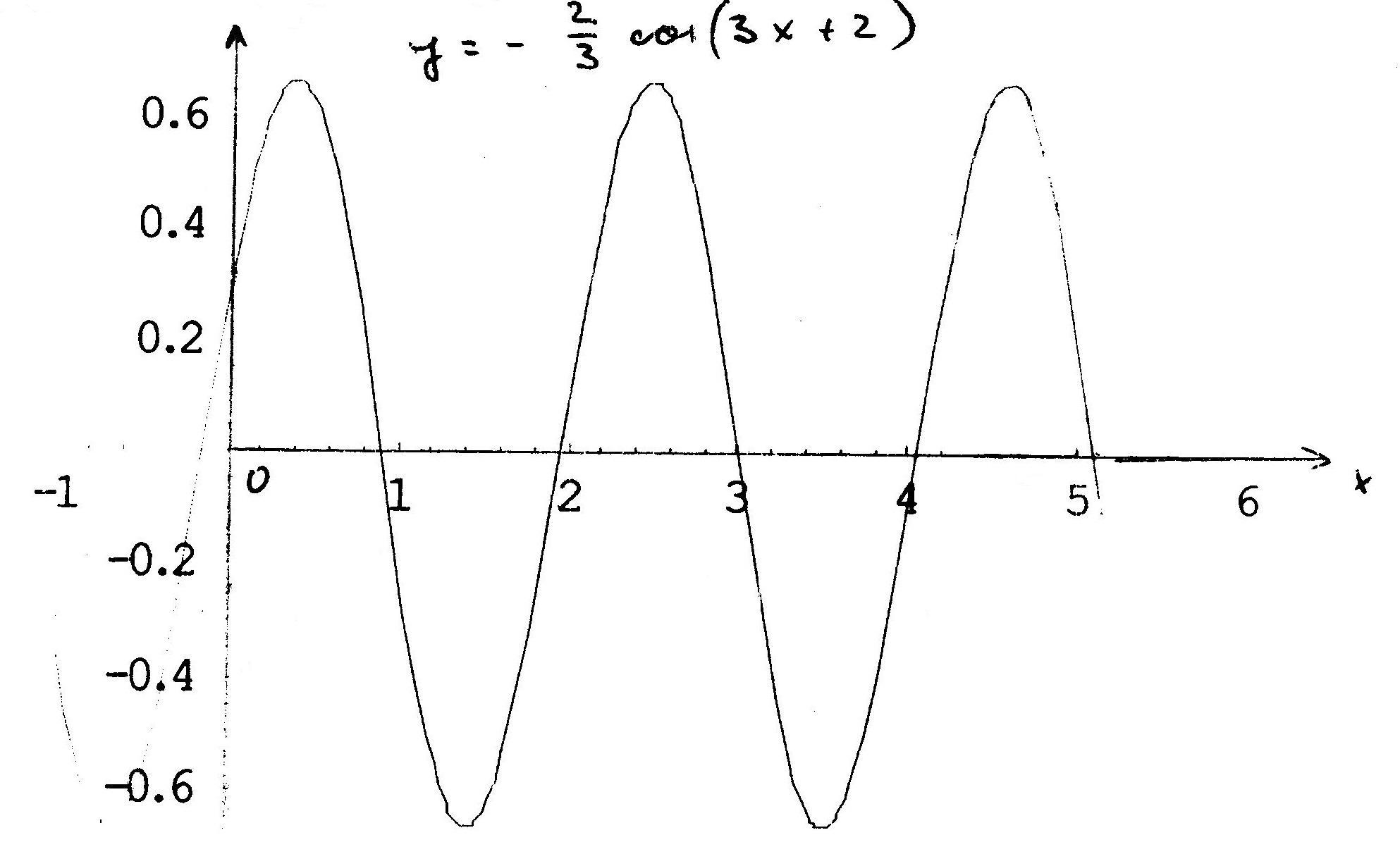
Построить график функции y=f(x) преобразованием графика функции y=cos x:

77.

Решение:

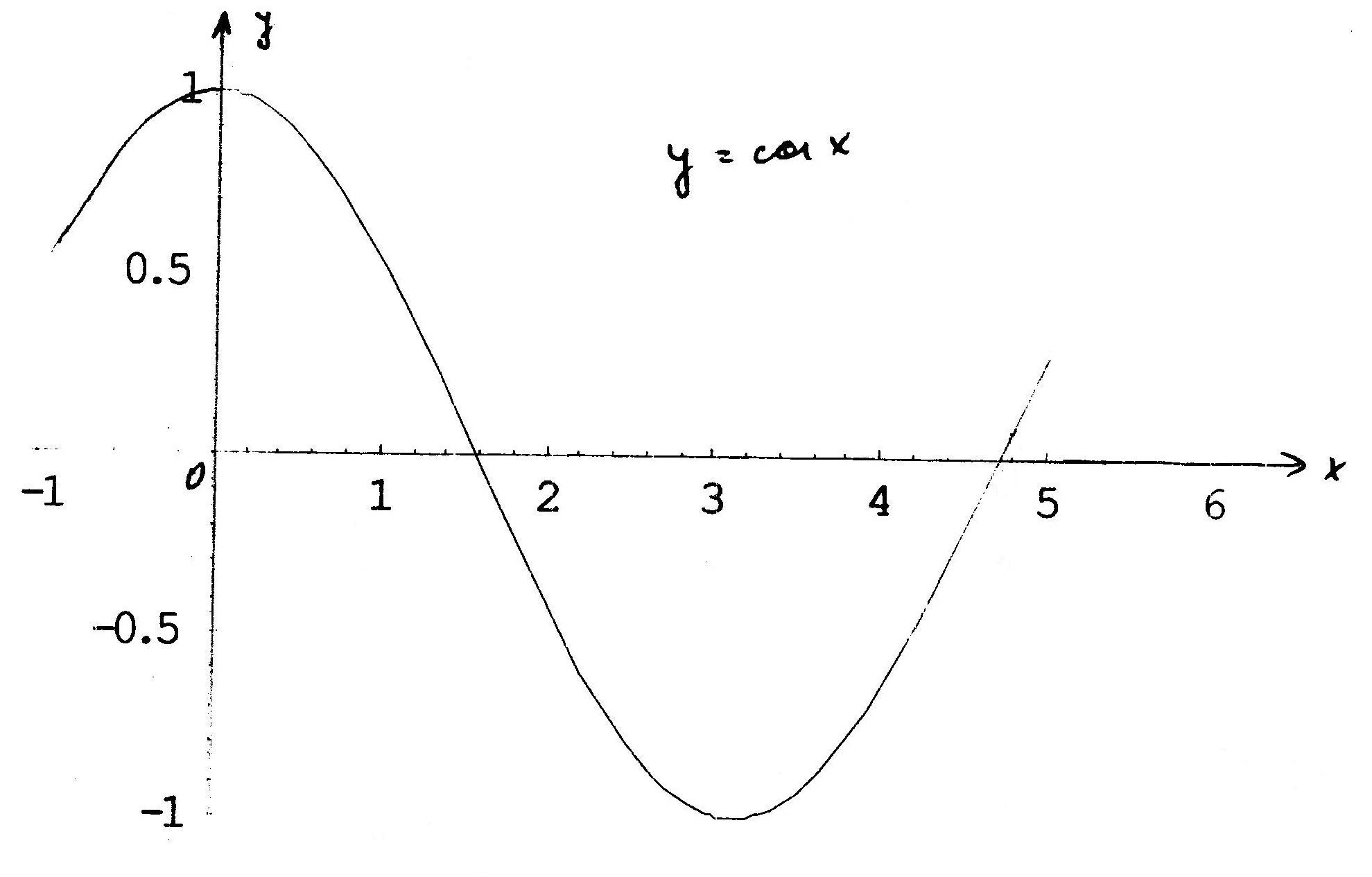
График сжат в 2/3 раза, отражен относительно оси ОХ, период сжат в 3 раза и начало сдвинуто на -2/3 радиан.

Задание 9

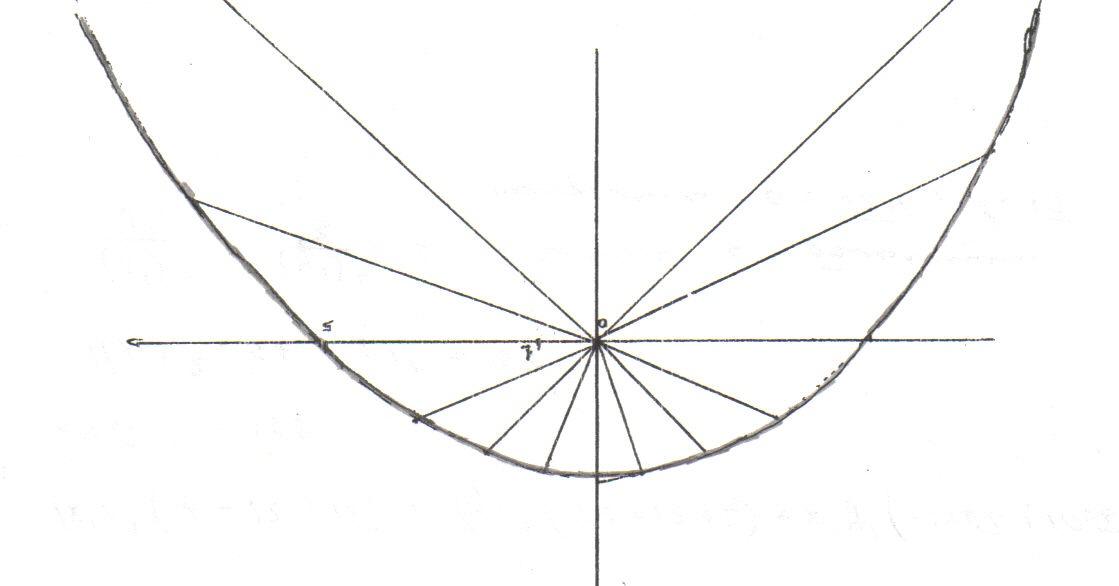
Дана функция r=f(x) на отрезке 0≤φ≤2π. Требуется: 1) построить график функции в полярной системе координат по точкам, давая φ значения через промежуток π/8, начиная от φ=0; 2) найти уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, и по уравнению определить, какая это будет линия.

Решение:

1)

	0
r	5	3,6	2,9	2,6	2,5	2,6	2,9	3,6	5	8,1	17,1	66	∞	66	17,1

r	8,1	5

2) ,

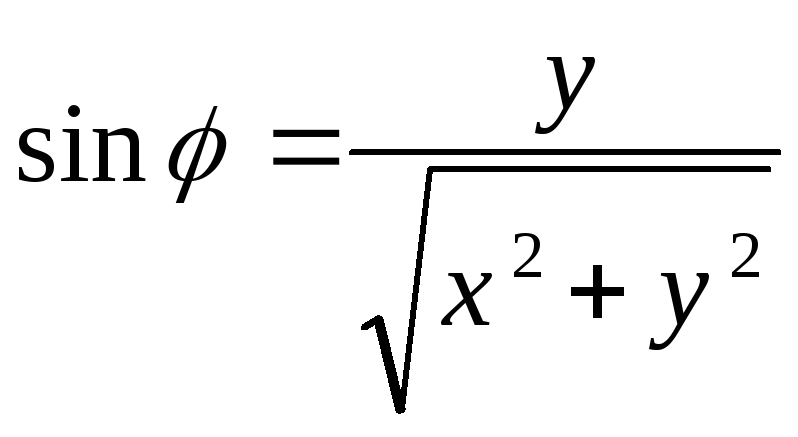
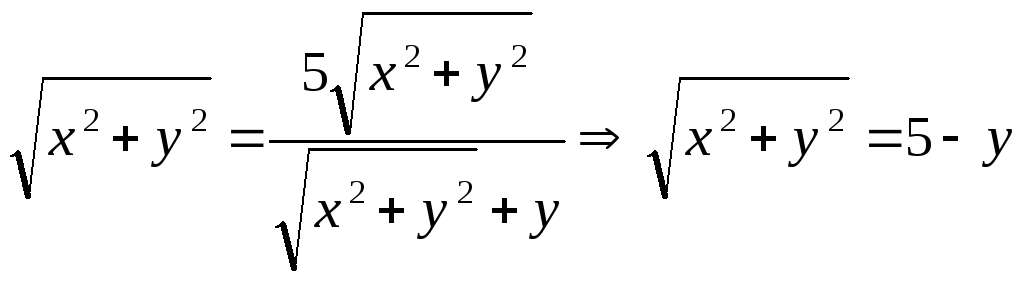
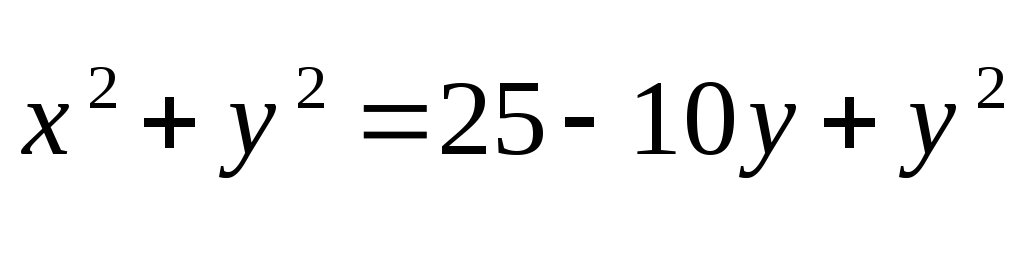
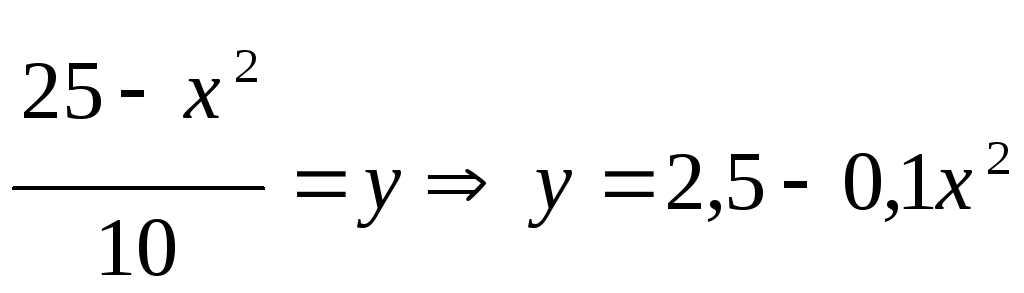- парабола.

3) Рисунок:

Задание 10

Найти указанные пределы, не пользуясь правилом Лопиталя:

Решение:

а)

б)

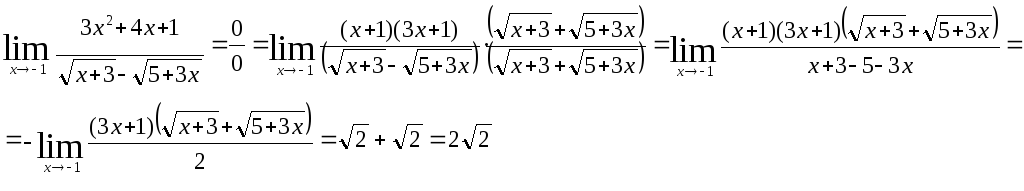
в)

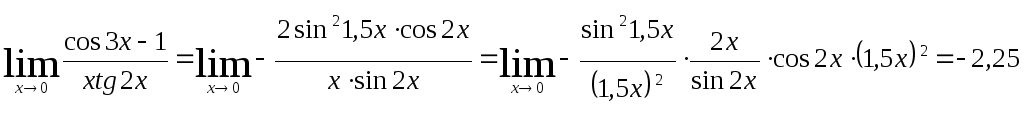
г)

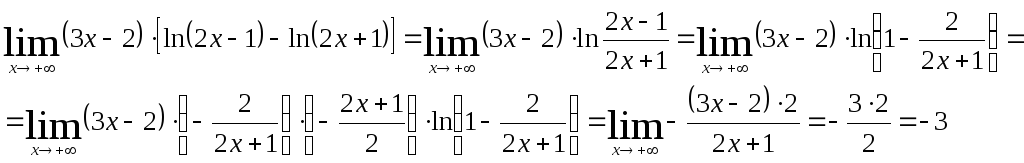
Задание 11

Заданы функция y=f(x) и два значения аргумента 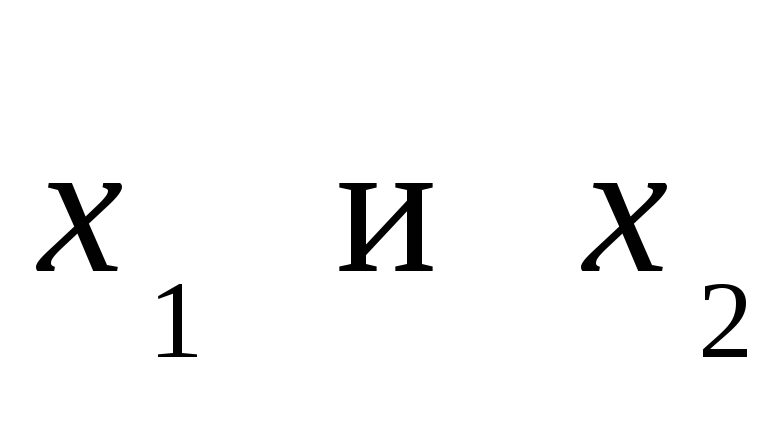. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого пиз данных значений аргумента; 2) в случае разрыва функции найти ее пределы при приближении к точке разрыва слева и справа; 3) сделать схематический чертеж.

Решение:

,

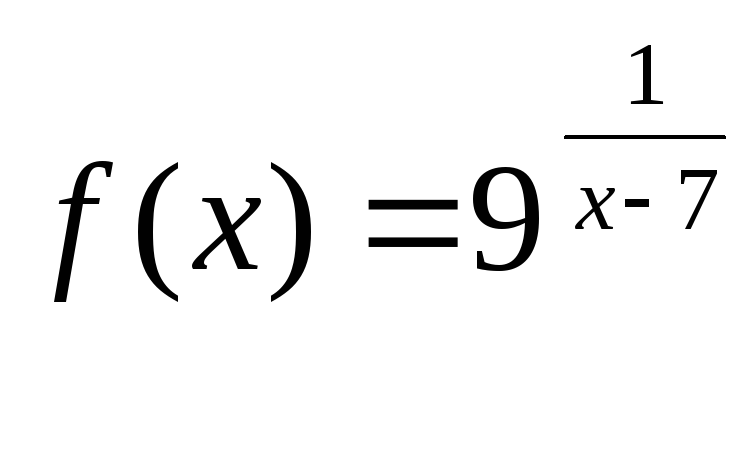
Функция в т. - непрерывна, т.к. и - непрерывны в этой точке

т. - точка разрыва

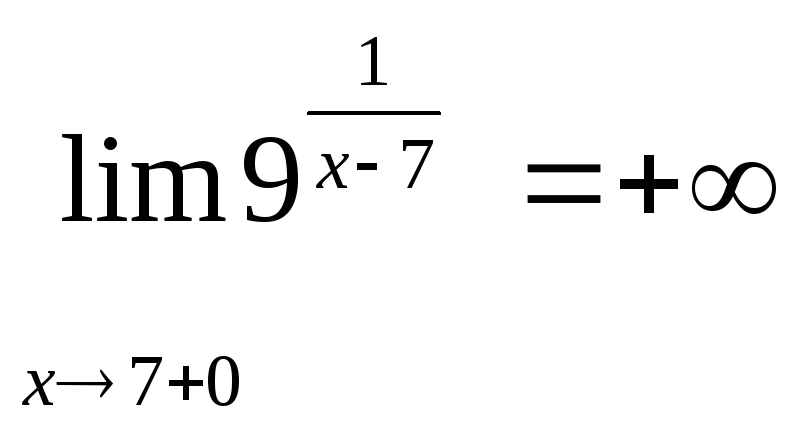
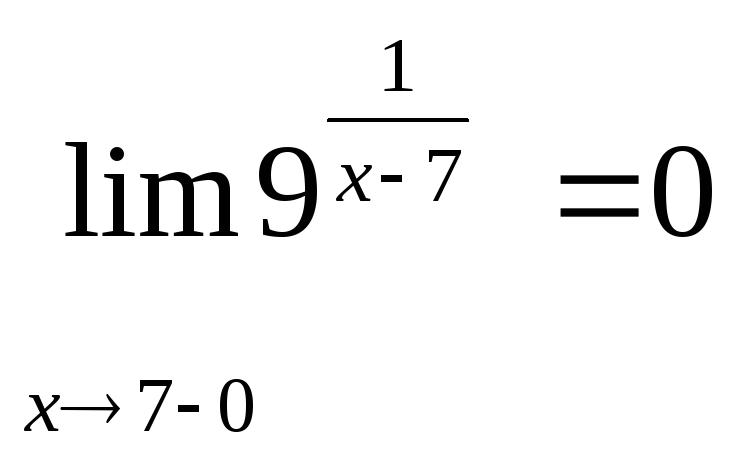
Значит - точка разрыва второго рода

Задание 12

Задана функция y=f(x) различными аналитическими выражениями для различных областей изменения независимой переменной. Найти точки разрыва функции, если они существуют. Сделать чертеж.

117.

Решение:

Функция sinx , непрерывна на (-∞; 0), функция х , непрерывна на [0; 2].

Исследуем f(x) в точке х=0

- y в точке - непрерывна

Исследуем f(x) в точке х=2

Точка - точка разрыва I рода.

Литература:

Беклемишев Д. В Курс аналитической геометрии и линей­ной алгебры.— 4^:е изд., переработ.— М: Наука. Главная редакция физико-математической литературы, 1980.—336 с.

15