КР №1 по вышке 2 вариант

Факультет: З и Д О

Курс:1

Вариант:2

Контрольная работа по высшей математике

Контрольная работа №1

Тема: ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

2. Даны четыре вектора и

в некотором базисе. Показать, что векторы образуют базис, и найти координаты вектора в этом базисе.

Решение. Базисом в пространстве являются любые три некомпланарных вектора. Условием компланарности трех векторов является равенство их смешанного произведения нулю. Итак, находим

 

Значит, векторы некомпланарны и образуют базис, то любой вектор можно представить в виде

Составим систему уравнений (1.1) в координатном виде

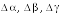
и найдем определители . Определитель найден выше.

Применяя правело Крамера, имеем

Значит:

12. Даны координаты вершин пирамиды A₁A₂A₃A₄. Найти: 1) длину ребра А₁А₂; 2) угол между ребрами А₁А₂ и А₁А₄; 3) угол между ребром А₁А₄ и гранью А₁А₂А₃; 4) площадь грани А₁А₂А₃; 5) объём пирамиды; 6) уравнения прямой А₁А₂; 7) уравнение плоскости А₁А₂А₃; 8) уравнения высоты, опущенной из вершины А₄ на грань А₁А₂А₃. Сделать чертёж, если

Решение. 1). Находим координаты вектора

и длину ребра

2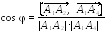). Угол между ребрами и вычисляется по формуле

из скалярного произведения.

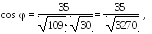
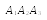Поэтому,

3



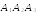). Угол между ребром и плоскостью - это угол между вектором и его ортогональной проекцией на грань.

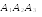
Вектор перпендикулярен грани , что вытекает из

определения векторного произведения векторов и :

Здесь Как и в предыдущем пункте, находим :

4). Площадь грани находим , используя геометрический смысл векторного произведения

5). Объем пирамиды численно равен одной шестой модуля

смешанного произведения векторов

6). Для составления уравнений прямой воспользуемся формулой уравнение прямой в пространстве, проходящей через две заданные точки и

:

В таком виде уравнения прямой называются каноническими. Они могут быть записаны и в виде

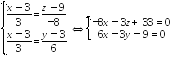
т.е. уравнение прямой как линии

и пересечения двух плоскостей.

7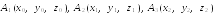). Для составления уравнения плоскости. , проходящей через три заданные точки :

8). Искомые уравнения высоты получим из канонических уравнений прямой, .

где - точка, лежащая на искомой

прямой, m, n, p - координаты вектора , параллельного искомой прямой. При этом в качестве точки возьмем точку , а в качестве вектора возьмем нормальный вектор плоскости , т.е. . . Имеем

.

9). Сделаем чертеж

22. На прямой 2x+y+11=0 найти точку, равноудалённую от двух данных точек A(1, 1) и B(3, 0).

Решение. Пусть точка М(х, у) лежащая на прямой 2х+у+11=0, равноудалена

От точек А и В , т.е. |AM| = |BM|.

Применив формулу отрезка в декартовой системе координат, получим:

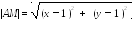
и

Тогда согласно условию составим систему уравнений:

После преобразований получим

Подставляя второе уравнение в первое имеем

тогда: , следовательно координаты искомой точки

32. Построить на плоскости область решений системы линейных неравенств.

Решение. Рассмотрим по отдельности каждое неравенство:

1). Чтобы решить неравенство 3х-у>9, построим прямую 3х-у=9 . Она проходит через две точки ( 3, 0) и (0, -9). При х=0 и у=0 неравенство является неверным. Следовательно, ему удовлетворяют все точки лежащие правее прямой 3х-у=9 и на прямой.

2). Решаем второе неравенство таким же образом, т.е. строим прямую

2х+3у<50 проходящую через две точки и .

Точка (0, 0) также является верным для неравенства 2х+3у<50 , следовательно, ему удовлетворяют все точки лежащие ниже прямой 2х+3у=50 и на этой прямой.

3). Находим точку А пересечения прямых 3х-у=9 и 2х+3у=50,решая систему

4). Наконец решаем неравенство –х+4у>19 . Для этого строим прямую

–х+4у=19 проходящую через точки и . Точка (0, 0) также

является неверным для неравенства –х+4у>19 следовательно, ему удовлетворяют все точки лежащие выше прямой ­–х+4у=19 и на этой прямой.

Решая системы уравнений:

Итак получили треугольник с вершинами А(7,30) , В(5б 24) и С(13, 8).

Данной системе неравенств удовлетворяют все точки внутри треугольника АВС и на его границе.

42. Составить уравнение линии, каждая точка которой находится вдвое дальше от точки A(3,0), чем от оси ординат.

Решение. Пусть М(x, y) – произвольная точка данной линии, P- основание перпендикуляра, проведенного через точку М к прямой x=0 . Расстояние точки М до точки А и до прямой x=0 определяется соответственно

формулами: . По условию задачи:

. Преобразуем это уравнение:

Выделим полные квадраты в левой части уравнения:

Если перейти к новым координатам, Y=y и X=x+1 , последнее уравнение

примет вид:

Полученное уравнение определяет гиперболу с полуосями a=2 и b= .