КР №1 Вар 9
.docxКонтрольная работа №1
Варианты
1 – 10. Даны три комплексных числа

 и
и
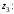
1) выполните действия в алгебраической, тригонометрической и показательной формах;
2)
найдите расстояние между точками
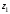 и
и
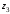 на комплексной плоскости.
на комплексной плоскости.
9.
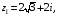


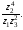
Решение.
Выполним действие в алгебраической форме.

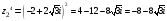
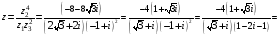
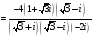
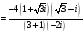
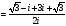
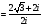 =
=
= =
=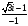 =
=
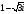 .
.
Выполним действие в тригономентрической форме.
Запишем комплексные числа в тригонометрической и показательных формах.
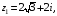
 ,
,
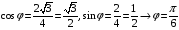 .
.
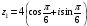 ,
,
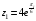

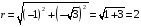 ,
,
 .
.
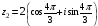 ,
,
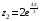 .
.
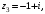
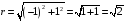 ,
,
 .
.
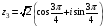 ,
,
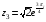 .
.


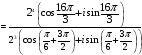

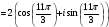 =
=


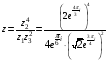 =
= .
.
Варианты 11 – 20. Решите уравнение на множестве комплексных чисел.
19.
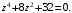
Решение.
 ,
,
 ,
,
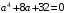 ,
,
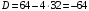
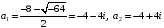 .
.
Решим
уравнения
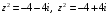
 ,
,
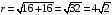 ,
,
 .
.
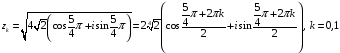
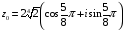 ,
,
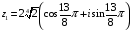
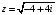 ,
,
 ,
,
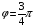 .
.

 ,
,

Варианты 21 – 30. Решите систему уравнений тремя способами:
1) методом Крамера;
2) методом обратной матрицы;
3) методом Гаусса.
29. 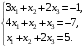
Решение.
Докажем совместность системы.
Найдем ранг основной и расширенной матрицы системы
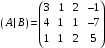

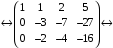

Ранг
основной матрицы равен рангу расширенной
матрицы и равен количеству неизвестных
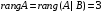 ,
следовательно, система совместна и
определена.
,
следовательно, система совместна и
определена.
Найдем решение системы с помощью формул Крамера. Воспользуемся формулами Крамера:
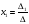 ,
,
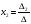 ,
,
 ,
где
,
где
 –
определитель, составленный из коэффициентов
при неизвестных.
–
определитель, составленный из коэффициентов
при неизвестных.
 =
=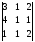 =
6+8+1–2–3–8= 2;
=
6+8+1–2–3–8= 2;
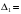
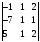 =
–6;
=
–6;
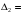
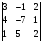 =
4;
=
4;

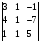 =
6
=
6
Найдем
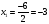 ,
,
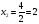 ,
,
 .
.
Получим (–3, 2, 3) – решение системы.
2. Решим систему методом Гаусса.
Запишем систему уравнений полученную после преобразования матрицы (А|В).
 ,
,
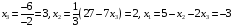 ,
,
Получим (–3, 2, 3) – решение системы.
3.
Решим систему матричным способом.
Запишем систему в матричной форме
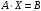 ,
,
где
 ,
,
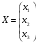 ,
,
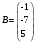 .
.
Решение
системы в матричной форме имеет вид
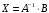 ,
где
,
где
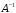 –
матрица, обратная матрице
–
матрица, обратная матрице
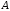 .
Найдем матрицу
.
Найдем матрицу
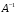 по формуле
по формуле
 =
=
 ,
где
,
где
 =
2 ,
=
2 ,
 –
алгебраическое дополнение к элементу.
–
алгебраическое дополнение к элементу.
|
|
|
|
|
|
|
|
|
|
|
|
Обратная
матрица имеет вид:
 =
=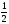
 .
.
Найдем
решение системы.
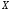 =
=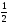

 =
=
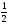
 =
= .
.
Ответ: (–3, 2, 3).
Варианты
31 – 40. Даны три вектора

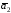 и
и
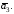 Докажите, что векторы
Докажите, что векторы
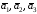 образуют базис, и определите, какая это
тройка векторов: правая или левая.
образуют базис, и определите, какая это
тройка векторов: правая или левая.
39.

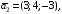
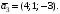
Решение.
Найдем смешенное произведение векторов по формуле
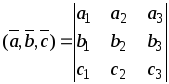 .
.

Поскольку смешенное произведение векторов не равно 0, то векторы некомпланарны, следовательно, образуют базис.
Смешенное произведение векторов равно –26 (меньше нуля), то векторы образуют левую тройку векторов.
Варианты
41 – 50. Даны координаты вершин
треугольной пирамиды
 Найдите:
Найдите:
1)
угол между ребрами
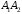 и
и

2)
площадь грани

3)
высоту, опущенную из вершины
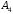 на грань
на грань
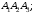
4)
уравнение прямой, проходящей через
ребро
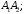
5)
уравнение плоскости, которой принадлежит
грань

6)
массу материальной треугольной пирамиды
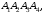 изготовленной из меди плотности
изготовленной из меди плотности
 (считая, что 1 масштабная единица в
системе координат равна 1 см).
(считая, что 1 масштабная единица в
системе координат равна 1 см).
49.
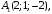


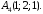
Решение.
Угол
между ребрами
![]() и
и
![]() вычисляется по формуле
вычисляется по формуле
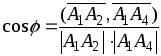 из скалярного произведения векторов
из скалярного произведения векторов
![]() и
и
![]() .
.
Найдем
координаты векторов
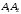 и
и
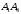 .
.
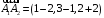 =
=
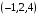 .
.
 =
=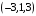 .
.
Тогда
 =
=
 =
=
=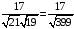 .
.
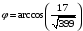 .
.
Площадь грани
![]() находим, используя геометрический смысл
векторного произведения
находим, используя геометрический смысл
векторного произведения
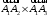 .
.
 =
=

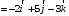
Тогда
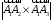 =
=
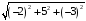 =
=
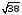 .
.
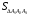 =
=
 .
.
Найдем
высоту, опущенную из вершины
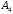 на грань
на грань
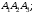

Объем пирамиды
![]() численно равен одной шестой модуля
смешанного произведения векторов
численно равен одной шестой модуля
смешанного произведения векторов
![]() ,
,
![]() ,
,
![]() ,
которое находится по формуле
,
которое находится по формуле
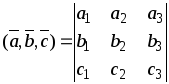 .
.
 =
=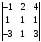 =
2.
=
2.

Искомое уравнение прямой
получим из канонических уравнений
прямой
 ,
где
,
где
![]() точка, лежащая на искомой прямой;
точка, лежащая на искомой прямой;
![]() координаты вектора
координаты вектора
![]() ,
параллельного искомой прямой. При этом
в качестве точки
,
параллельного искомой прямой. При этом
в качестве точки
![]() возьмем точку
возьмем точку
 ,
а в качестве вектора
,
а в качестве вектора
![]() возьмем вектор
возьмем вектор
 = (–1, 1, 1).
= (–1, 1, 1).
Имеем
 .
.
Для составления уравнения
плоскости
![]() воспользуемся формулой
воспользуемся формулой
 ,
где
,
где
![]() координаты точки
координаты точки
![]() ,
,
![]() координаты точки
координаты точки
![]() ,
,
![]() координаты точки
координаты точки
![]() .
.
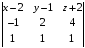 =
= .
.
 =0
– уравнение плоскости.
=0
– уравнение плоскости.
Найдем
массу материальной треугольной пирамиды
 изготовленной из меди плотности
изготовленной из меди плотности
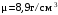 (считая, что 1 масштабная единица в
системе координат равна 1 см)
(считая, что 1 масштабная единица в
системе координат равна 1 см)
 г.
г.
Варианты 51 – 60. Изобразите геометрическое место точек, заданных уравнением:
1) на плоскости;
2) в пространстве.
59.
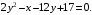
Решение.
Опредедим геометрическое место точек на плоскости
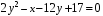 ,
,
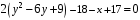 ,
,
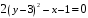 ,
,
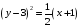 – парабола
с вешиной в точке (-1, 3)
– парабола
с вешиной в точке (-1, 3)

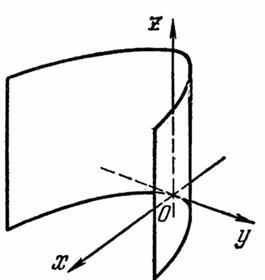
В пространстве – эллептический цилиндр

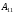 =
=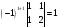
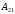 =
=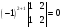
 =
=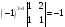
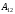 =
=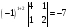
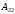 =
=
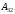 =
=
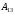 =
=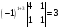
 =
=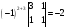
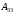 =
=