Лекція з курсу «Автоматизація проектування комп’ютерних систем»

Тема: Математичне забезпечення процесу синтезу проектних рішень:

• Постановка задачі параметричного синтезу;

• Огляд методів оптимізації;

• Постановка задач структурного синтезу;

• Методи структурного синтезу в САПР.

• Постановка задачі параметричного синтезу;

Місце процедур синтезу в проектуванні. Суть проектування полягає в ухваленні проектних рішень, які забезпечують виконання майбутнім об'єктом вимог, що пред'являються до нього. Синтез проектних рішень - основа проектування; від успішного виконання процедури синтезу у визначальній мірі залежать споживчі властивості майбутньої продукції. Звичайно, аналіз - необхідна складова частина проектування, яка забезпечує верифікацію ухвалюваних проектних рішень. Саме аналіз дозволяє отримати необхідну інформацію для цілеспрямованого виконання процедур синтезу в ітераційному процесі проектування. Тому синтез і аналіз нерозривно зв'язані.

Синтез підрозділяють на параметричний і структурний. Проектування починається із структурного синтезу, при якому генерується принципове рішення. Таким рішенням може бути зовнішній вигляд майбутнього літального апарату, або фізичний принцип дії сенсора, або одна з типових конструкцій двигуна, або функціональна схема мікропроцесора. Але ці конструкції і схеми вибирають в параметричному вигляді, тобто без визначення числових значень параметрів елементів. Тому перш ніж приступити до верифікації проектного рішення, потрібно задати або розрахувати значення цих параметрів, тобто виконати параметричний синтез. Прикладами результатів параметричного синтезу можуть служити геометричні розміри деталей в механічному вузлі або в оптичному приладі, параметри електрорадіоелементів в електронній схемі, параметри режимів різання в технологічній операції і т.д.

У випадку якщо за наслідками аналізу проектне рішення визнається неостаточним, то починається процес послідовних наближень до прийнятного варіанту проекту. У багатьох застосуваннях для покращення проекту зручніше варіювати значення параметрів елементів, тобто використовувати параметричний синтез на базі багатоваріантного аналізу. При цьому завдання параметричного синтезу може бути сформульована як завдання визначення значень параметрів елементів, якнайкращих з позицій задоволення вимог технічного завдання при незмінній структурі проектованого об'єкту. Тоді параметричний синтез називають параметричною оптимізацією або просто оптимізацією. Якщо параметричний синтез не приводить до успіху, то повторюють процедури структурного синтезу, тобто на чергових ітераціях коректують або перевибирають структуру об'єкту.

Критерії оптимальності. У САПР процедури параметричного синтезу виконуються або людиною в процесі багатоваріантного аналізу (у інтерактивному режимі), або реалізуються на базі формальних методів оптимізації (у автоматичному режимі). В останньому випадку знаходять застосування декілька постановок завдань оптимізації.

Найбільш поширеною є детермінована постановка: задані умови працездатності на вихідні параметри Y і потрібно знайти номінальні значення проектних параметрів N, до яких відносяться параметри всіх або частини елементів проектованого об'єкту. Це завдання базової оптимізації. В окремому випадку, коли вимоги до вихідних параметрів задані нечітко, до величин, які розраховуються, можуть бути віднесені також норми вихідних параметрів, що фігурують в їх умовах працездатності.

Якщо проектуються вироби для подальшого серійного виробництва, то важливого значення набуває такий показник, як відсоток випуску придатних виробів в процесі виробництва. Очевидно, що успішне виконання умов працездатності в номінальному режимі не гарантує їх виконання при врахуванні виробничих похибок, параметрів елементів, що задаються допусками. Тому метою оптимізації стає максимізація процесу виходу придатних, а до результатів рішення задачі оптимізації відносяться не тільки номінальні значення проектних параметрів, але і їх допуски. Базове завдання оптимізації ставиться як завдання математичного програмування:

де F(X) - цільова функція, X - вектор керованих (проектних) параметрів, - функції-обмеження, Dx -допустима область в просторі керованих параметрів. Запис (4.1) інтерпретується як завдання пошуку екстремуму цільової функції шляхом варіювання керованих параметрів в межах допустимої області.

Таким чином, для виконання розрахунку номінальних значень параметрів необхідно:

1. сформулювати завдання у вигляді (4.1),

2. вирішити задачу пошуку екстремуму F(X).

Складність постановки оптимізаційних проектних завдань обумовлена наявністю у проектованих об'єктів декількох вихідних параметрів, які можуть бути критеріями оптимальності, але в завданні (4.1) цільова функція повинна бути одна. Іншими словами, проектні завдання є багатокритеріальними, і виникає проблема зведення багатокритеріального завдання до однокритеріального.

Застосовують декілька способів вибору критерію оптимальності.

У частковому критерію серед вихідних параметрів один вибирають як цільової функції, а умови працездатності решти вихідних параметрів відносять до обмежень завдання (4.1).

Ця постановка цілком прийнятна, якщо дійсно можна виділити один найбільш критичний вихідний параметр. Але в більшості випадків позначається недолік часткового критерію (рис. 4.1). На цьому рисунку представлений двовимірний простір вихідних параметрів y1 і y2, для яких задані умови працездатності y1 < T1 і y2 < T2. Крива C( є межею досяжних значень вихідних параметрів. Це обмеження об'єктивне і пов'язано з існуючими фізичними і технологічними умовами виробництва. Область, в межах якої виконуються всі реалізуючі умови і умови працездатності, називають областю працездатності. Множина точок простору вихідних параметрів, з яких неможливе переміщення, що приводить до поліпшення всіх вихідних параметрів, називають областю компромісів, або областю Парето. Ділянка кривої C( (див. мал. 4.1) відноситься до області Парето.

Якщо як цільову функція в ситуації рис. 4.1. вибрати параметр y1, то результатом оптимізації будуть параметри N, відповідні точці В. Але це межа області працездатності і, отже, при нестабільності внутрішніх і зовнішніх параметрів велика імовірність виходу за межі області працездатності. Звичайно, результати можна покращити, якщо застосовувати так званий метод поступок, при якому як обмеження приймають умову працездатності з скоректованою нормою у вигляді y2 < T2 + Е, де Е- поступка. Але виникає проблема вибору значень поступок, тобто результати оптимізації матимуть суб'єктивний характер. Очевидно, що ситуація не зміниться, якщо цільовою функцією буде вибраний параметр y2, - оптимізація приведе в точку А.

Адитивний критерій; об'єднує (згортає) всі вихідні параметри (часткові критерії) в одну цільову функцію, що є зваженою сумою часткових критеріїв

де - ваговий коефіцієнт, m - число вихідних параметрів. Функція (4.2) підлягає мінімізації, при цьому якщо умова працездатності має вид yj > Tj, то < 0.

Недоліки аддитивного критерію - суб'єктивний підхід до вибору вагових коефіцієнтів і неврахування вимог ТЗ оскільки в (4.2) не входять норми вихідних параметрів.

Аналогічні недоліки властиві і мультиплікативному критерію, цільова функція якого має вигляд

Неважко бачити, що якщо прологарифмувати (4.3), то мультиплікативний критерій перетворюється на аддитивний.

Переважнішим є максімінний критерій як цільову функцію якого приймають вихідний параметр, найбільш неблагополучний з позицій виконання умов працездатності. Для оцінки ступеня виконання умови працездатності j-го вихідного параметра вводять запас працездатності цього параметра Sj і цей запас можна розглядати як нормований j-й вихідний параметр. Наприклад (тут і далі для лаконічності викладу передбачається, що всі вихідні параметри приведені до вигляду, при якому умови працездатності стають нерівностями у формі yj < Tj ):

де у ном j - номінальне значення, а Sj - деяка характеристика розсіяння j-го вихідного параметра, наприклад, трисигмовий допуск. Тоді цільова функція в максимінному критерії є

Тут запис [1: m] означає множина цілих чисел в діапазоні від 1 до m. Завдання (4.1) при максимінном критерії конкретизується таким чином:

де допустима область Dx визначається тільки прямими обмеженнями на керовані параметри xi: xi min < xi < xi max .

- Огляд методів оптимізації;

Класифікація методів математичного програмування. У САПР основними методами оптимізації є пошукові методи, які базуються на покроковій зміні керованих параметрів де, в більшості випадків, приріст вектора керованих параметрів обчислюється за формулою

Xk - значення вектора керованих параметрів на к-му кроці, h - крок, а g(Xk) - напрям пошуку. Отже. якщо виконуються умови збіжності, то реалізується покрокове (ітераційне) наближення до екстремуму.

Методи оптимізації класифікують по ряду ознак.

Залежно від числа керованих параметрів розрізняють методи одновимірної і багатовимірної оптимізації. Для одномірної оптимізації керований параметр єдиний, для багатомірної розмір вектора X не менше ніж два. Реальні завдання в САПР багатовимірні, методи одновимірної оптимізації грають допоміжну роль на окремих етапах багатовимірного пошуку.

Розрізняють методи умовної і безумовної оптимізації по наявності або відсутності обмежень. Для реальних завдань характерна наявність обмежень, проте методи безумовної оптимізації також представляють інтерес, оскільки завдання умовної оптимізації можуть бути зведені до завдань без обмежень.

Залежно від числа екстремумів розрізняють завдання одно- і багатоекстремальні. Якщо метод орієнтований на визначення локального екстремуму, то такий метод відноситься до локальних методів. Якщо ж результатом є глобальний екстремум, то метод називають методом глобального пошуку. Задовільні по обчислювальній ефективності методи глобального пошуку для загального випадку відсутні і тому на практиці в САПР використовують методи пошуку локальних екстремумів.

Залежно від того, використовуються при пошуку похідні цільової функції по керованих параметрах чи ні, розрізняють методи декількох порядків. Якщо похідні не використовуються, то має місце метод нульового порядку, якщо використовуються перші або другі похідні, то відповідно метод першого або другого порядку. Методи першого порядку називають також градієнтними, оскільки вектор перших похідних F(X) по N є градієнт цільової функції

Конкретні методи визначаються наступними чинниками:

1) способом обчислення напряму пошуку g(Xk) у формулі (4.6);

2) способом вибору кроку h;

3) способом визначення закінчення пошуку.

Визначальним чинником є перший з перерахованих в цьому списку, він детально описаний нижчим.

Крок може бути або постійним, або вибиратися виходячи з одновимірної оптимізації - пошуку мінімуму цільової функції у вибраному напрямі g(Xk).

Закінчення пошуку зазвичай здійснюють за правилом: якщо впродовж r підряд кроків, що йдуть, траєкторія пошуку залишається в малому околі поточної точки пошуку Xk, то пошук слід припинити, отже, умова закінчення пошуку має вигляд

Методи одномірної оптимізації. До методів одномірної оптимізації відносяться методи дихотомічного ділення, золотого перетину, чисел Фібоначі, поліноміальній апроксимації і ряд їх модифікацій.

Хай заданий відрізок [A,b], на якому є один мінімум (у загальному випадку непарне число мінімумів). Згідно методу дихотомічного ділення (рис. 4.3,а) відрізок ділять навпіл і в точках, віддалених від центру: відрізок на величину допустимої похибки q, розраховують значення цільової функції F(C+q) і F(C-q). Якщо вияявиться, що F(C+q) > F(C-q), то мінімум знаходиться на відрізку [A, C], якщо F(C+q) < F(C-q), то мінімум - на [C,b], якщо F(C+q)= F(C-q) - на [C-q,С+q]. Таким чином, на наступному кроці замість відрізку [A,b] потрібно досліджувати звужений відрізок [A, C], [C,В] або [C-q,С+q]. Кроки повторюються, поки довжина відрізок не зменшиться до величини похибки q. Таким чином, потрібно не більше ніж N кроків, де N - найближче до log((B-A)/q) ціле значення, але на кожному кроці цільову функцію слід обчислювати двічі.

По методу золотого перетину (рис. 4.3,б) усередині відрізку [A,b] виділяють дві проміжні точки С1 і D1 на відстані s = al від його кінцевих точок, де L = B-A - довжина відрізку. Потім обчислюють значення цільової функції F(x) в точках С1 і D1. Якщо F(C1)< F(D1), то мінімум знаходиться на відрізку [A,d1], якщо F(C1)> F(D1), то - на відрізку [C1,b], якщо F(C1)= F(D1) - на відрізку [ C1, D1].

Отже, замість відрізку [A,b] тепер можна розглядати відрізок [A,d1], [C1,b] або [C1, D1], тобто довжина відрізку зменшилася не менше ніж в L/(L-AL)= 1/(1-a) разів. Якщо підібрати значення ) так, що в отриманому відрізку меншої довжини одна з проміжних крапок співпаде з проміжною крапкою від попереднього кроку, тобто у разі вибору відрізок [A,d1] точка D2 співпаде з точкою C1, а у разі вибору відрізок [C1,b] точка C2 - з точкою D1, то це дозволить скоротити число обчислень цільової функції на всіх кроках (окрім першого) в 2 рази.

Умова набуття такого значення ) формулюється таким чином , звідки з врахуванням того, що , маємо а = 0,382. Це значення і називають золотим перетином.

Таким чином, потрібно не більше ніж N кроків і N+1 обчислень цільової функції, де N можна розрахувати, використовуючи співвідношення при заданій похибці Е визначення екстремуму.

Згідно методу чисел Фібоначчі, використовують числа Фібоначчі Ri (послідовність яких утворюється за правилом Ri+2 = Ri+1 + Ri при R0 = R1 = 1, тобто ряд чисел Фібоначчі має вигляд 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144....) Метод аналогічний методу золотого перетину з тією відмінністю, що коефіцієнт а рівний відношенню , початкове значення i визначається з умови, що Ri повинне бути найменшим числом Фібоначчі, що перевищує величину (B-A)/Е, де Е - задана допустима похибка визначення екстремуму. Так, якщо (В-А) / Е = 100, то початкове значення i = 12, оскільки R1= 144, і а = 55/144 = 0,3819, на наступному кроці буде а = 34/89 = 0,3820 і так далі

По методу поліноміальної апроксимації при апроксимації F(x) квадратичним поліномом

вибирають проміжну точку С і в точках А, В, С обчислюють значення цільової функції. Далі вирішують систему з трьох рівнянь, отриманих підстановкою в (4.7) значень А,В,С замість, і обчислених значень функції замість Р(х). В результаті стають відомими значення коефіцієнтів аk у (4.7) і, виходячи з умови dР(x)/dx = 0, визначають екстремальну точку F полінома. Наприклад, якщо точка : вибрана в середині відрізку [A,b], то .

Методи безумовної оптимізації. Серед методів нульового порядку в САПР знаходять застосування методи Розенброка, конфігурацій (Хука-Джівса), деформованого багатогранника (Нелдера-Міда), випадкового пошуку. До методів з використанням похідних відносяться методи найшвидшого спуску, спряжених градієнтів, змінної метрики.

Метод Розенброка є покращеним варіантом покоординатного спуску.

Метод покоординатного спуску характеризується вибором напрямів пошуку по черзі вздовж всіх n координатних осей, крок розраховується на основі одномірної оптимізації, критерій закінчення пошуку |X_k X_{k n}| < Е, де Е - задана точність визначення локального екстремуму, n - розмірність простору керованих параметрів. Траєкторія покоордінатного спуску для прикладу двомірного простору керованих параметрів показана на рис. 4.4, де Xk - точки на траєкторії пошуку, xi - керовані параметри. Цільова функція представлена своїми лініями рівного рівня, біля кожної лінії записано відповідне нею значення F(X). Очевидно, що Q є точка мінімуму.

При використанні методу покоординатного спуску велика імовірність “застрявання” пошуку на дні яру далеко від точки екстремуму (Яром називають частину простору керованих параметрів, в якій спостерігаються слабкі зміни похідних цільовій функції по одних напрямах і значні зміни із зміною знаку - по деяких іншим напрямам. Знак похідної міняється в точках, що належать дну яру). На рис. 4.5 видно, що після попадання в точку C, розташовану на дні яру, подальші кроки можливі лише в напрямах аа або bb, але вони приводять до погіршення цільової функції. Отже, пошук припиняється в точці А. В той же час при сприятливій орієнтації дна яру, а саме при положенні однієї з координатних осей, близькому до паралельності з дном яру, пошук виявляється дуже швидким. Ця ситуація показана на рис. 4.6.

Метод Розенброка полягає в такому повороті координатних осей, щоб одна з них виявилася квазіпаралельною дну яру. Такий поворот здійснюють на основі даних, отриманих після серії з n кроків покоординатного спуску. Положення нових осей si може бути отримане лінійним перетворенням колишніх осей xi: вісь s1 співпадає по напряму з вектором Xk+n - Xk; решта осей вибирає з умови ортогональності до N1 і один до одного.

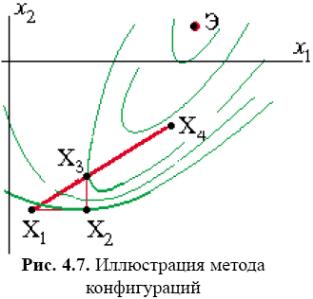
Іншою вдалою модифікацією покоордінатного спуску є метод конфігурацій. Відповідно до цього методу спочатку виконують звичайну серію з n кроків покоордінатного спуску, потім роблять додатковий крок у напрямі вектора Xk - Xk-n, як показано на рис. 4.7, де додатковий крок виконують у напрямі вектора X3 - X1, що і приводить в точку X4.

Пошук екстремуму методом деформованого багатогранника базується на побудові багатогранника з (n + 1) вершинами на кожному кроці пошуку, де n - розмірність простору керованих параметрів. На початку пошуку ці вершини вибирають довільно, на подальших кроках вибір підпорядкований правилам методу.

Ці правила пояснюються рис. 4.8 на прикладі двомірного завдання оптимізації. Вибрані вершини початкового трикутника: X1, X2, X3. Нова вершина X4 знаходиться на промені, проведеному з гіршої вершини X1 (з вершини з найбільшим значенням цільової функції) через центр тяжіння SM багатогранника, причому рекомендується X4 вибирати на відстані d від SM, рівному |SM-X1|. Нова вершина X4 замінює гіршу вершину X1. Якщо виявляється, що X4 має краще значення цільової функції серед вершин багатогранника, то відстань d збільшують. На рисунку саме ця ситуація і збільшення d дає точку X5. У новому багатограннику з вершинами X2, X3, X5 гіршою є вершина X2, аналогічно отримують вершину X6, потім вершину X7 і так далі Якщо нова вершина виявиться гіршою, то в багатограннику потрібно зберегти кращу вершину, а довжини всіх ребер зменшити, наприклад удвічі (стягання багатогранника до кращої вершини). Пошук припиняється при виконанні умови зменшення розмірів багатогранника до деякої межі.

Випадкові методи пошуку характеризуються тим, що напрям пошуку g вибирається випадково. Особливістю методу найшвидшого спуску є виконання кроків в градієнтному напрямі

,

крок h вибирається оптимальним за допомогою одномірної оптимізації.

При використанні методу найшвидшого спуску, як і більшості інших методів, ефективність пошуку істотно знижується в ситуаціях ярів. Траєкторія пошуку набуває зигзагоподібного вигляду з повільним просуванням вздовж дна яру у бік екстремуму. Щоб підвищити ефективність градієнтних методів, використовують декілька прийомів.

Один з прийомів, використаний вметоді спряжених градієнтів (відомому як метод Флетчера-Рівса), який базується на понятті зв'язаності векторів. Вектори А і В називають Q-спряженими, якщо , де Q - позитивно визначена квадратна матриця того ж порядку, що і розмір N векторів (окремий випадок зв'язаності - ортогональність векторів, коли Q є одиничною матрицею порядку N), AT -вектор-стрічка, B - вектор-стовпець.

Особливість зв'язаних напрямів для Q = K, де K - матриця Гессі (матриця часткових похідних другого порядку цільової функції по керованих параметрах), при задачах з квадратичною цільовою функцією F(X) полягає в наступному: одномірна мінімізація F(X) послідовно по N зв'язаних напрямах дозволяє знайти екстремальну точку не більше, ніж за N кроків.

Підставою для використання пошуку по Г-спряжених напрямах є те, що для функцій F(X) загального вигляду може бути застосована квадратична апроксимація, що на практиці виливається у виконання пошуку більш, ніж за N кроків.

Приклад. Пошук екстремуму виконують відповідно до формули

На першому кроці пошуку вибирають S1 = - grad F(X0) і знаходять точку Х1. На другому кроці по формулі (4.14) розраховують w1, по формулах (4.9) і (4.8) визначають S2 і Х2 і т. д.

Метод змінної метрики (метод Девідона-Флетчера-Пауела) можна розглядати як результат удосконалення методу другого порядку - методу Ньютона.

Метод Ньютона базується на використанні необхідних умов безумовного екстремуму цільової функції F(X)

Вираз (4.15) є системою рівнянь алгебри, для вирішення якої можна застосувати відомий чисельний метод, званого методом Ньютона. Корінь системи (4.15) є стаціонарна точка, тобто можливе рішення екстремальної задачі. Метод Ньютона є ітераційним, він базується на лінеаризації (4.15) в околі поточної точки пошуку Хk

Вираз (4.16) - це система лінійних рівнянь алгебри. Її корінь є чергове наближення Хk+1 до вирішення .

Якщо процес сходиться, то рішення досягається за мале число ітерацій, закінченням яких служить виконання умови . Головний недолік методу - висока трудомісткість обчислення і звернення матриці Г, до того ж її обчислення чисельним диференціюванням супроводжується суттєвими похибками, що знижує швидкість збіжності.

У методі змінної метрики замість важко обчислюваної зворотної матриці Гессі використовують деяку більш легко обчислювану матрицю N, тобто

E - одинична матриця. Початкове значення матриці N0 = E. Матрицю N коректують на кожному кроці, тобто

Можна показати, що наближується до , - до при де n – розмірність простору керованих параметрів. Через n кроків, потрібно знову починати з .

Необхідні умови екстремуму. У задачах безумовної оптимізації необхідні умови є рівністю нулю градієнта цільової функції

grad F(X)= 0.

У загальній задачі математичного програмування (4.1) необхідні умови екстремуму (умовами Куна-Таккера), формулюються таким чином: для того, щоб точка Э була екстремальною точкою опуклої задачі математичного програмування (ЗМП), необхідна наявність ненегативних коефіцієнтів ui, таких, що

і при цьому дотримувалися обмеження завдання, а також виконувалася умова

де m - число обмежень типу нерівностей, L - те ж рівності, коефіцієнти aj > 0.

За приведеним абстрактним формулюванням умов ховається геометричний сенс, що досить просто розуміється. Дійсно, розглянемо спочатку випадок з обмеженнями тільки типу нерівностей. Якщо максимум знаходиться усередині допустимої області R, то, вибираючи все ui = 0, добиваємося виконання (4.17); якщо ж точка максимуму Q лежить на межі області R, то, як видно з лівої частини рис. 4.9, цю точку завжди відповідним підбором ненегативних ui можна помістити всередину оболонки, натягнутої на градієнти цільової функції F(X) і функцій-обмежень .

Навпаки, якщо точка не є екстремальною, то (4.17) не можна виконати при будь-якому виборі позитивних коефіцієнтів ui (права частина рис. 4.9, де дана точка Х лежить поза опуклою оболонкою, натягнутою на градієнти). Облік обмежень типу рівності очевидний, якщо додається остання з вказаних в (4.18) сума.

Методи пошуку умовних екстремумів. Широко відомий метод множників Лагранжа, орієнтованого на пошук екстремуму за наявності обмежень типу рівності , тобто на вирішення задачі

Cуть методу полягає в перетворенні завдання умовної оптимізації (4.19) в завдання безумовної оптимізації за допомогою утворення нової цільової функції

де — вектор множників Лагранжа, L - число обмежень.

Необхідні умови екстремуму функції Ф(N):

Система (4.20) містить n+l рівнянь алгебри, де n - розмірність простору керованих параметрів, її вирішення дає шукані координати екстремальної точки і значення множників Лагранжа. Проте при чисельному рішенні (4.20), що має місце при використанні алгоритмічних моделей, виникають ті ж труднощі, що і в методі Ньютона. Тому в САПР основними методами вирішення ЗМП є методи штрафних функцій і проекції градієнта.

Основна ідея методів штрафних функцій - перетворення завдання умовної оптимізації в завдання безумовної оптимізації шляхом формування нової цільової функції Ф(N) введенням в початкову цільову функцію F(X) спеціальним чином вибраної функції штрафу S(X):

де r - множник, значення якого можна змінювати в процесі оптимізації.

Серед методів штрафних функцій розрізняють методи внутрішньої і зовнішньої точки. Згідно методам внутрішньої точки (методи бар'єрних функцій) початкову для пошуку точку можна вибирати тільки всередині допустимої області, а для методів зовнішньої точки як усередині, так і поза допустимою областю (важливо лише, щоб в ній функції цільова і обмежень були б визначені). Ситуація появи бар'єру в цільової функції Ф(х) і співвідношення між умовним в точці x2 і безумовним в точці x1 мінімумами F(х) в простому одномірному випадку ілюструється рис. 4.10.

Приклади штрафних функцій:

1) для методу внутрішньої точки при обмеженнях

де m - число обмежень типу нерівностей;

2) для методу зовнішньої точки при таких же обмеженнях

тут штраф зводиться до включення у Ф(х) суми квадратів активних (тобто порушених) обмежень;

3) у разі обмежень типу рівності

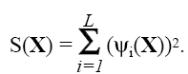
Чим більшим є коефіцієнт r, тим точніше рішення задачі, проте при великих r може погіршуватися її обумовленість. Тому на початку пошуку зазвичай вибирають помірні значення r, збільшуючи їх в околицях екстремуму.

Основний варіант методу проекції градієнта орієнтований на завдання математичного програмування з обмеженнями типу рівності.

Пошук при виконанні обмежень здійснюється в (n-m) мірному підпросторі, де n - число керованих параметрів, m - число обмежень, при цьому рух здійснюється в напрямку проекції градієнту цільової функції F(x) на гіперплощину, дотичну до гіперповерхні обмежень (точніше до перетину гіперповерхонь обмежень).

Пошук мінімуму починають із спуску з початкової точки на гіперповерхню обмежень. Далі виконують крок у вказаному вище напрямі (крок уздовж гіперповерхні обмежень). Оскільки цей крок може привести до помітного порушення обмежень, знов повторюють спуск на гіперповерхню обмежень і так далі Іншими словами, пошук полягає у виконанні пар кроків, кожна пара включає спуск на гіперповерхню обмежень і рух уздовж гіперповерхні обмежень.

Ідею методу легко пояснити для випадку пошуку в двомірному просторі при одному обмеженні . На рис. 4.11 це обмеження представлене товстою лінією, а цільова функція - сукупністю тонших ліній рівного рівня. Спуск зазвичай здійснюють по нормалі до гіперповерхні обмежень (в даному випадку до лінії обмеження). Умова закінчення пошуку базується на зіставленні значень цільової функції в двох послідовних точках, що отримуються після спуску на гіперповерхню обмежень.

Розглянемо питання, які стосується отримання аналітичних виразів для напрямів спуску і руху уздовж гіперповерхні обмежень.

Спуск. Необхідно з поточної точки пошуку попасти в точку , яка є найближчою до точкою на гіперповерхні обмежень, тобто вирішити задачу при умові , котре після лінеаризації в околицях точки А має вигляд .

Використовуючи метод множників Лагранжа, позначаючи і враховуючи, що мінімізація відстані рівнозначна мінімізації скалярного добутку U на U, запишемо

Рух вздовж гіперповерхні обмежень. Крок в гіперплощині D, дотичній до гіперповерхні обмежень, слід зробити у напрямі вектора S, на якому цільова функція зменшується в найбільшій мірі при заданому кроці h. Зменшення цільової функції при переході з точки А в нову точку С підраховують, використовуючи формулу лінеаризації F(X) в околицях точки А: , де grad F(A) TS - приріст F(X), який потрібно мінімізувати, варіюючи напрями S

де варіація S здійснюється в межах гіперплощини D; і S - ортогональні вектори. Отже, мінімізацію (4.23) необхідно виконувати при обмеженнях

Останнє обмеження говорить про те, що при пошуку напряму руху, вектор S повинен лише вказувати цей напрям, тобто його довжина неістотна (хай S - одиничний вектор).

Для вирішення (4.23) використовуємо метод множників Лагранжа

є проектуючою матрицею, а вектор S, розрахований по (4.27), - проекцію градієнта grad F(A) на гіперповерхню обмежень.

Окремим випадком застосування методу проекції градієнта є задача оптимізації з максимінним критерієм. Дійсно, для пошуку екстремуму функції мінімуму

де Zj - нормована величина j-го вихідного параметра yj, зручно застосовувати метод проекції градієнта. Як обмеження завдання в початковій постановці фігурують тільки прямі обмеження Тут, Хmaxi і Хmini- граничні значення допустимого діапазону варіювання параметра,i. В процесі пошуку, якщо мінімальною є функція Zq(X) і траєкторія пошуку перетинає гребінь

то пошук продовжується у напрямі проекції градієнта функції Zq(X) на гіперповерхню гріб ня (4.28).