
Контрольная работа вариант 18
.docИсходные данные:
![]()
![]()
![]()
![]()
![]()
Классический метод: ![]()
![]()

Рассмотрим схему до коммутации.
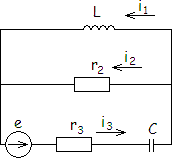
Так как в цепи включён источник синусоидального напряжения, расчёт проводим символическим методом.
Реактивное сопротивление индуктивности:
![]()
![]()
Реактивное сопротивление ёмкости:
![]()
![]()
Комплексная амплитуда источника:
![]()
Комплексное сопротивление цепи относительно источника:
![]()
![]()
Комплексная амплитуда тока в ветви источника определится по закону Ома:
![]()
![]()
Комплексную амплитуду напряжения на ёмкости определим по закону Ома:
![]()
![]()
Мгновенное значение напряжения на ёмкости запишется в виде:
![]()
Полагая в последнем выражении t=0-, получим величину напряжения на ёмкости непосредственно перед коммутацией:
![]()
По законам коммутации напряжение на ёмкости не может изменяться скачком. Следовательно,
![]()
Комплексная амплитуда тока в ветви с индуктивностью:
![]()
![]()
Мгновенное значение тока в индуктивности запишется в виде:
![]()
Полагая в последнем выражении t=0-, получим величину тока в индуктивности непосредственно перед коммутацией:
![]()
По законам коммутации ток в индуктивности не может изменяться скачком. Следовательно,
![]()
Принуждённые составляющие тока в индуктивности и напряжения на ёмкости определим по данной схеме:

Комплексное сопротивление цепи относительно источника:
![]()
![]()
Комплексная амплитуда тока в ветви источника определится по закону Ома:
![]()
![]()
Комплексную амплитуду напряжения на ёмкости определим по закону Ома:
![]()
![]()
Мгновенное значение напряжения на ёмкости запишется в виде:
![]()
Комплексную амплитуду тока в ветви с индуктивностью
определим по правилу плеч:
![]()
![]()
Мгновенное значение тока в цепи с индуктивностью запишется в виде:
![]()
Замыкаем накоротко зажимы источника ЭДС. Разрываем ветвь с ёмкостью. Комплексное входное сопротивление относительно разрыва запишется в виде
![]()
Полагая в последнем выражении j=p, получим:
![]()
После выполнения алгебраических преобразований получим характеристическое уравнение второго порядка:
![]()
Определим дискриминант квадратного уравнения:
![]()
![]()
Найдем корни характеристического уравнения:

![]()

![]()
По виду корней характеристического уравнения записывается свободная составляющая переходного процесса. Так как число корней равно двум и они действительны, то:
![]()
Полный переходной процесс в индуктивности равен сумме принуждённой и свободной составляющих:
![]()
В последнем уравнении неизвестными являются А1 и А2, следовательно, для их однозначного определения необходимо второе уравнение. Получим его дифференцированием первого:
![]()
Полагая в вышеприведённых уравнениях t=0+, получим:
![]()
![]()
![]()
Производная тока в индуктивности в момент коммутации относится к зависимым начальным условиям. Для определения зависимых начальных условий составим систему уравнений по законам Кирхгофа для момента времени t=0+ послекоммутационной схемы:

![]()
![]()
![]()
![]()
Выразим первое выражение через третье:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Подставляя численные значения найденных ранее независимых начальных условий i1(0+), uc(0+) и значение e(0+)=0, получим:
![]()
![]()
Тогда уравнения для определения постоянных интегрирования примут вид:
![]()
![]()
![]()
Постоянные интегрирования будут равны:
![]()
![]()
Окончательное выражение для переходного тока в индуктивности запишется в виде:
![]()
Переходной процесс по напряжению по ёмкости рассчитывается аналогично. Записываем выражение для uc(t) как сумму двух составляющих:
![]()
Принуждённая составляющая переходного процесса определена выше. Свободную составляющую ищем в виде суммы экспонент. С учётом этого:
![]()
Второе уравнение, необходимое для однозначного определения постоянных интегрирования, получим дифференцированием первого:
![]()
Полагая в обоих уравнениях t=0+, получим:
![]()
![]()
![]()
Производная напряжения на ёмкости в момент коммутации относится к зависимым начальным условиям. Определим её значение по выражению:
![]()
Значение i3(0+) определим из системы уравнений по законам Кирхгофа для момента времени t=0+, записанной выше. Тогда:
![]()
Уравнения для определения постоянных интегрирования примут вид:
![]()
![]()
![]()
Решая систему уравнений, определим постоянные интегрирования:
![]()
![]()
Окончательное выражение для переходного напряжения в емкости запишется в виде:
![]()
Окончательные выражения для напряжения в индуктивности и тока в емкости определим по следующим выражениям:
![]()
![]()
![]()
![]()
При построении графиков переходных процессов, прежде всего, необходимо определить их длительность. Теоретически переходные процессы длятся бесконечно долго, практически же оканчиваются за время, равное трём постоянным времени tпп=3. За это время свободная составляющая переходного процесса будет иметь значение, составляющее 5% от значения при t=0+.
Постоянная времени определяется как величина, обратная минимальному по модулю корню характеристического уравнения:
![]()
![]()
Следовательно, длительность переходного процесса для рассматриваемой задачи:
![]()
![]()
Построим графики переходных процессов:
Ток в индуктивности:

Напряжение в ёмкости:

Напряжение в индуктивности:

Ток в ёмкости:

