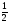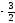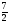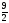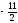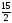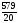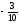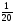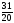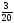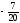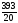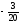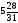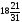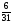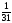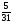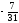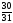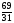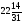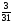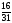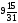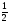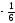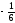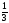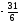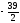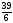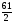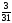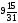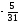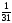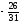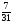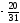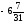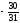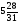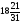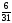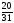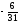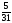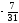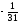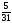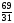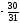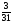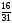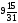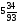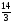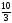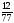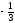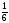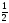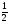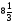Министерство образования республики Беларусь
Учреждение образования
«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ»
Институт информационных технологий
Специальность ИТИуТС
Контрольная работа
По курсу «Математические основы теории систем»
Вариант № 18
Студент-заочник 2 курса
Группы № 082424
ФИО Милашевский
Владимир Сергеевич
Адрес г. Минск
Ул. Рогачевская 5-20
Тел. 8029-773-96-18
Минск, 2012
Содержание:
1) Задание 1: Линейное программирование……………………………………..3
2) Задание 2: Нелинейное программирование…………………………………14
Список использованной литературы……………………………………………19
Задание 1: Линейное программирование
Найти оптимальный план x* и экстремальное значение функции F(x).
Построить задачу, двойственную к исходной, решить её и сравнить решения прямой и двойственной задач.
Если решение не является целочисленным, получить целочисленное решение путём введения дополнительных ограничений по методу Гомори.
Вариант 18.
Условия задачи: F(x) = 3x1 + x2 -6x3 (max)
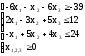
Математическая модель выглядит следующим образом:
max{F(x) = 3x1 + x2 - 6x3 | -6x1 - x2 - 6x3 ≥ -39; 2x1 - 3x2 + 5x3 ≤ 12;
-x1 + 5x2 + 4x3 ≤ 24; x1,2,3 ≥ 0}.
Для удобства заполнения симплекс-таблицы приведем ограничения к виду «≤», умножив обе части неравенства на «-1».
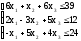
Приведем ограничения к виду равенств, введя дополнительные переменные со знаком «+», т.к. ограничения вида «≤»:
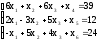
Матрицы A, Bи CTвыглядят следующим образом:
A= ;B
=
;B
=
 ;СT
=
;СT
=
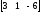 ;
;
Если дополнительная переменная со знаком «-», то все коэффициенты перед переменными xi и свободный член bj заносятся с противоположным знаком.
Если цель минимизация, то коэффициенты функции цели заносятся без изменения знака.
Симплекс-таблица выглядит следующим образом:
|
БП |
СЧ |
НП | ||
|
x1 |
x2 |
x3 | ||
|
x4 x5 x6 |
39 12 24 |
6 2 -1 |
1 -3 5 |
6 1 4 |
|
Fmax |
0 |
-3 |
-1 |
6 |
За базисные переменные принимаем дополнительные переменные x4, x5,x6. А переменные x1, x2,x3 будут являться небазисными.
Свободные члены определяют решение задачи.
1 шаг: Производится поиск базисного решения. Т.к. все свободные члены положительны, значит, решение является допустимым. Переходим сразу к шагу 5 для нахождения оптимального решения.
5 шаг: Признаком оптимальности является неотрицательность переменных в F-строке. c1, c2 < 0. Следовательно, решение не является оптимальным.
В базис будет включаться та из небазисных переменных, которая находится в столбце с элементом cl, которому соответствует максимальное абсолютное значение.
В данной задаче это элемент c1 = -3< 0.Ведущий столбец x1.
Выбор
ведущей строки определяется минимальным
симплексным отношением
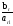 .
Следует рассматривать только положительные
симплексные отношения.
.
Следует рассматривать только положительные
симплексные отношения.
В данной задаче минимальное симплексное отношение получается в строке
x5 = 6.
Таким образом, ведущая строка x5. Ведущий элемент a21 = 2.
Производим пересчет симплекс-таблицы:
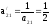 ;
;
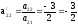 ;
;
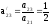 ;
;
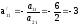 ;
;
 ;
;
 ;
;
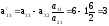 ;
;
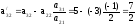 ;
;
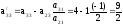 ;
;
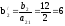 ;
;
 ;
;
 ;
;
 ;
;
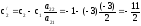 ;
;
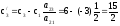 ;
;
 ;
;
Новая симплекс-таблица выглядит следующим образом:
|
БП |
СЧ |
НП | ||
|
x5 |
x2 |
x3 | ||
|
x4
x1
x6 |
3
6
30 |
-3
|
10
|
3
|
|
Fmax |
18 |
|
|
|
|
БП |
СЧ |
НП | ||
|
x5 |
x4 |
x3 | ||
|
x2
x1
x6 |
|
|
|
|
|
Fmax |
|
|
|
|
|
БП |
СЧ |
НП | ||
|
x6 |
x4 |
x3 | ||
|
x2
x1
x5 |
|
|
|
|
|
Fmax |
|
|
|
|
Fmax
=
 .
.
Оптимальный план:
x2
=
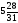
x1
=
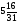
x5
=

Выводим условия двойственной задачи:
F(x) = 3x1 + x2 -6x3 (max)

Так как задача максимизации, то условия приводим к виду «≤»:
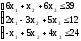
Матрицы AT, Bи Cвыглядят следующим образом:
AT=
 ;B
=
;B
=
 ;С
=
;С
= ;
;
Количество переменных в двойственной задаче равно количеству переменных в прямой, и наоборот.
Тогда ATY ≥ C примет вид:

Функция
цели F(y)
= BTY
=

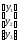 =
39y1
+ 12y2
+ 24y3
(min)
=
39y1
+ 12y2
+ 24y3
(min)
Так как среди ограничений прямой задачи нет равенств и на все переменные наложено условие неотрицательности, то двойственная задача симметрична.
Далее решение производится симплекс-методом.
Вводим дополнительные переменные и приводим ограничения к виду равенств.
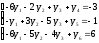
Так как цель минимизация, коэффициенты функции цели заносятся в таблицу без изменения знака.
|
БП |
СЧ |
НП | ||
|
y1 |
y2 |
y3 | ||
|
y4 y5 y6 |
-3 -1 6 |
-6 -1 -6 |
-2 3 -5 |
1 -5 -4 |
|
Fmin |
0 |
39 |
12 |
24 |
1шаг: Так как не все элементы столбца свободных членов положительны, значит допустимое базисное решение не найдено.
Производим поиск допустимого базисного решения, используя шаг 2.
2шаг: Производим пересчет симплекс-таблицы:
Определяем какую небазисную переменную введем в базис и какую базисную переменную выведем из базиса. Для этого выбираем любой из отрицательных элементов столбца свободных членов.
Пусть это будет b1= -3 < 0.Просматриваем строку, в которой находится этот элемент, и выбираем любой отрицательный элемент.
Пусть это будет a11 = -6 < 0.
Если в строке нет отрицательных элементов, то задача не имеет решения.
Приоритетом в выборе элементов является максимальное абсолютное значение модуля элемента.
Таким образом, ведущим элементом будет являться элемент a11 = -6. Ведущая строка y4, ведущий столбец – y1. Из базиса исключается переменная y4, в базис вводится переменная y1.
Производим пересчет симплекс-таблицы.
Новая симплекс-таблицы выглядит следующим образом:
|
БП |
СЧ |
НП | ||
|
y4 |
y2 |
y3 | ||
|
y1
y5
y6 |
9 |
-1 |
-3 |
-5 |
|
Fmin |
|
|
-1 |
|
|
БП |
СЧ |
НП | ||
|
y4 |
y2 |
y5 | ||
|
y1
y3
y6 |
|
|
|
|
|
Fmin |
|
|
|
|
Оптимальное решение найдено.
Fmin
=
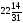 .
.
Оптимальный план:
y1
=
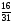 .
.
y3
=
 .
.
y6
=
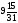 .
.
Решения прямой и двойственной задачи совпадают.
Решение задачи без условия целочисленности приведено в пункте 1.
Составим
дополнительное ограничение по строке,
соответствующей переменной x2,
так как у неё наибольшая дробная часть
{x2}
=
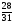 .
.
Решение производим по алгоритму Гомори для полностью целочисленной задачи.
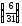 x6
+
x6
+ x4
+
x4
+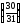 x3
≥
x3
≥
или
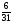 x6
+
x6
+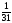 x4
+
x4
+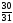 x3
≥
x3
≥
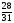
Приведем к виду равенства, введя дополнительную переменную x7 и домножим обе части неравенства на «-1»:
 x6
x6
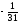 x4
x4
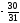 x3
+x7
= -
x3
+x7
= -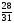
Расширенная симплекс-таблица выглядит следующим образом:
|
БП |
СЧ |
НП | ||
|
x6 |
x4 |
x3 | ||
|
x2
x1
x5
x7 |
|
|
|
|
|
Fmax |
|
|
|
|
|
БП |
СЧ |
НП | ||
|
x7 |
x4 |
x3 | ||
|
x2
x1
x5
x6 |
5
|
1
|
0
|
0
0
-1
5 |
|
Fmax |
22 |
|
|
|