
Задание 2: Нелинейное программирование
Построить область допустимых значений переменных.
Найти максимальное значение функции F(x) без учета ограничений на переменные, используя:
а) метод наискорейшего спуска
б) метод Ньютона
Процесс оптимизации начинать с точки x0.
Найти максимальное значение функции F(x) с учетом системы ограничений задачи, используя:
а) метод допустимых направлений Зойтендейка
б) условия теоремы Куна-Таккера
Процесс оптимизации начинать с точки x0.
Вариант 18.
F(x)
=
 +5
+5 +4
+4
 +5
+5 +7
+7

x1,2≥ 0
x0 = [3;2]
|
x1 |
0 |
7 |
-7 |
|
x2 |
2 |
4 |
0 |
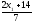
|
x1 |
0 |
7 |
6,2 |
|
x2 |
-31 |
4 |
0 |


2)
а) Находим составляющие вектора градиента функции:

Так как экстремумом функции будет являться её минимум, градиент будем использовать с противоположным знаком.
1
шаг: Движение
осуществляется из x0вдоль
 в
новую точкуx1:
в
новую точкуx1:
Градиент в точке x0равен:


Координаты точки x1определяются выражением:

Величину
шага
 определим
из условия:
определим
из условия:


 =
=

В результате точка x1:

2 шаг:
Градиент в точке x1равен:


Координаты точки x2 определяются выражением:
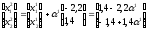
Величину
шага
 определим
из условия:
определим
из условия:



В результате точка x2:

3 шаг:
Градиент в точке x2равен:


Координаты точки x3 определяются выражением:

Величину
шага
 определим
из условия:
определим
из условия:


В результате точка x3:

В точке х3 функция достигает значения
Fmax
=
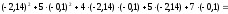 -5,91;
-5,91;
Метод наискорейшего спуска неэффективен при приближении к точке экстремума, поэтому существует погрешность.
б) Так как функция цели квадратичная, экстремум будет найден за один шаг.



H-1=
 ,
гдеdetH–
определитель матрицы H.
,
гдеdetH–
определитель матрицы H.
detH = 2∙10 - 4∙4 = 20 – 16 = 4.
AdjH – присоединенная к H матрица (транспонированная матрица алгебраических дополнений).
Найдем алгебраические дополнения элементов матрицы H:
 ,
тогда:
,
тогда:
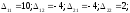
Тогда
AdjH= ;
H-1
=
;
H-1
=
 ;
;
 ;
;

Fmax = -8,5;
Равенство градиента нулю показывает, что найденная точка является экстремальной, а решение – оптимальным. Исходя из этого, можно построить графики функций и наглядно увидеть, что метод наискорейшего спуска оставляет погрешность и эффективен он только для задач с большим удалением начальной точки от точки максимума.

3) а)
Учитывая, что экстремум функции будет являться её минимумом, будем использовать градиент с противоположным знаком.
Градиент в точке х0 равен:



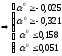
Выбираем наиболее сильные условия:

Находим
значение
 как в методе наискорейшего спуска.
как в методе наискорейшего спуска. .
Данное значение не принадлежит найденному
интервалу, поэтому
.
Данное значение не принадлежит найденному
интервалу, поэтому .
.
Точка х1 равна:

Таким образом, точка попадает на ограничение х2 = 0.
Градиент в точке х1 равен:


Движение в этом направлении выводит за пределы ОДЗП, поэтому очередная точка поиска будет производиться в направлении S1:


Координаты новой точки определятся выражением:
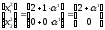
Определим
интервал изменения параметра
 при которомx2
принадлежит области допустимых значений
переменных:
при которомx2
принадлежит области допустимых значений
переменных:


 =>
=>


Выбираем наиболее сильные условия:
-2
≤

 ≤ 4,2
≤ 4,2
Находим
величину

 ,
которая обеспечит максимум функцииF(x)
в направлении S1:
,
которая обеспечит максимум функцииF(x)
в направлении S1:
Для этого в функцию цели подставляем координаты точки x2:
F(
 )
=
)
=


 ;
;
Значение

 = -4,5 не принадлежит найденному интервалу,
поэтому принимаем значение
= -4,5 не принадлежит найденному интервалу,
поэтому принимаем значение
 равным граничному значению,
равным граничному значению,
 .
.

Градиент в точке x2 равен:

Его направление перпендикулярно направлению вектора S1. Следовательно, данная точка является оптимальным решением.
Функция
достигает экстремума в точке
 .
Точка экстремума лежит на пересечении
ограничивающих прямых
.
Точка экстремума лежит на пересечении
ограничивающих прямых и
и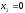 .
.
Fmin = 0.

б) Составим функцию Лагранжа:
Так
как экстремум функции будет являться
минимумом, то производная
 ,
а производная
,
а производная .
.



Запишем условия теоремы Куна-Таккера:


|
БП |
СЧ |
НП | |||
|
x1 |
x2 |
λ1 |
λ2 | ||
|
v1
v2
w1
w2 |
5
7
14
31 |
-2
-4
-2
5 |
-4
-10
7
-1 |
2
-7
0
0 |
-5
1
0
0 |
Решение, определяемое последней таблицей, соответствует допустимому базисному решению v1= 5; v2= 7; w1=14; w2=31; x1=x2= λ 1= λ2= 0.
Выполняется
условие x1∙v1=x2∙v2
= λ1∙w1=λ2∙w2
= 0, поэтому
 является оптимальным решением задачи.
является оптимальным решением задачи.
При этом Fmin= 0.
Список использованной литературы:
1) Полный конспект лекций. Павлова А. В. БГУИР.
2) Математические основы теории систем, алгебраические структуры и матричные методы. Авторы: Ушаков, Хабалов, Дударенко, СПбГУ ИТМО 2005г.
