
- •Факультет информационных технологий и управления
- •1 Математическое описание линейных систем
- •1.1 Дифференциальное уравнение системы.Характеристическое уравнение и его корни
- •1.2 Разложение передаточной функции на сумму простых слагаемых. Вычисление импульсной переходной характеристики ω(t) спомощью обратного преобразования Лапласа и переходной характеристикиh(t)
- •1.3 Построение лачх и лфчх
- •1.4 Уравнение состояния в нормальной форме,схема моделирования
- •1.5 Уравнение состояния в канонической форме,
- •1.6 Решение уравнения состояния в нормальной и канонической формах
- •1.7 Проверка: одинаково ли значение коэффициента усиления по передаточной функции, переходной характеристике,моделям в пространстве состояний, аналитической записи импульсной переходной характеристики
- •2 Линейное программирование
- •2.1 Математическая модель задачи. Нахождение оптимального плана х* и экстремального значения функции
- •2.2 Построение и решение задачи, двойственной к исходной. Сравнение решения прямой и двойственной задач
- •2.3 Получение целочисленного решения путем введения дополнительных ограничений по методу Гомори
- •3.2.2 Метод Ньютона-Рафсона
- •3.3 Нахождение экстремального значения функцииF(X) с учетом системы ограничений задачи
- •3.3.1 Метод допустимых направлений Зойтендейка
- •3.3.2 Метод линейных комбинаций
- •3.3.3 Условия теоремы Куна-Таккера
- •4 Тексты программ в среде matlab
- •4.1 Математическое описание линейных систем
- •4.2 Линейное программирование
- •4.3 Нелинейное программирование
1.2 Разложение передаточной функции на сумму простых слагаемых. Вычисление импульсной переходной характеристики ω(t) спомощью обратного преобразования Лапласа и переходной характеристикиh(t)
Получим разложение передаточной функции на сумму простых слагаемых:

Найдём a, b, c.
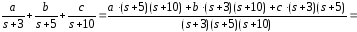
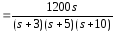 .
.
Следовательно,
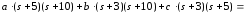
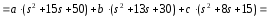
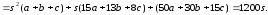
Получим систему уравнений:
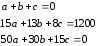

Решая эту систему, получим корни:

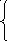
Передаточная функция:

Импульсная переходная характеристика w(t) – это процесс изменения сигнала на выходе при подаче на вход δ-функции. Ее можно найти в результате обратного преобразования Лапласа, примененного к каждому слагаемому передаточной функции.
В
соответствии с таблицами соответствия
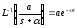 ,тогда:
,тогда:
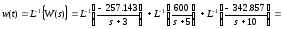
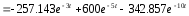
Переходная характеристика h(t) – это процесс изменения сигнала на выходе при подаче на вход единичного ступенчатого воздействия. Ее можно вычислить следующим образом:
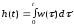 ,
,
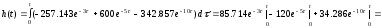

таким образом аналитическая форма переходной характеристики имеет вид:
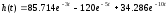 .
.
Переходную
характеристику можно также вычислить
следующим образом: так как на вход
подается единичное ступенчатое
воздействие, а преобразование по Лапласу
1(t)
это
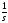 ,
то
,
то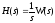 ,
получим такой же результат.
,
получим такой же результат.
Выполним проверку:
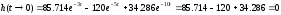 -верно;
-верно;
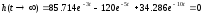 -
верно.
-
верно.
1.3 Построение лачх и лфчх
При определении частотных характеристик подразумевается, что на входе и выходе системы сигналы являются гармоническими.
Амплитудно-частотная характеристика (АЧХ) показывает, как изменяется отношение выходного сигнала к входному в зависимости от частоты.
Фазочастотная характеристика (ФЧХ) показывает изменение сдвига фаз между входным и выходным сигналами в зависимости от частоты.
ЛАЧХ строится в двойных логарифмических шкалах. По одной логарифмической оси откладывается круговая частота ω, по другой значение L(ω)=20lgK, выраженное в децибелах. Асимптотическая ЛАЧХ состоит из отрезков прямых линий с наклонами кратными 20дБ/дек.
Преобразуем передаточную функцию к следующему виду:
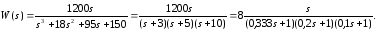
Теперь
она представляет собой произведение
трех апериодических и одного форсирующего
звена с постоянными времени ;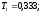
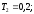
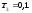 Коэффициент
усиления К=8. Сопрягающие частоты звеньев
равны
Коэффициент
усиления К=8. Сопрягающие частоты звеньев
равны
;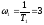 ;
;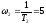 ;
;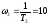 .
.
Далее необходимо правильно разметить оси и отметить на оси ω сопрягающие частоты. ЛАЧХ приведена на рис. 1.1, а.
 Рисунок
1.1 –Асимптотические ЛАЧХ (а) и ЛФЧХ (б)
Рисунок
1.1 –Асимптотические ЛАЧХ (а) и ЛФЧХ (б)
Первая
линия в области низких частот проводится
через точку ω=1;L(ω)=20lgK.
Через эту точку проводится первый
наклон, и он равен ,
где
- количество интегрирующих звеньев. Так
как есть дифференцирующее звено (=-1),
то первый наклон будет +1. Он идет с
наклоном +1доL(ω)=20lgK=20lg8=18
частоты
,
где
- количество интегрирующих звеньев. Так
как есть дифференцирующее звено (=-1),
то первый наклон будет +1. Он идет с
наклоном +1доL(ω)=20lgK=20lg8=18
частоты
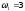 .
Эта частота относится к апериодическому
звену Следовательно, наклон изменится
на -1. ЛАЧХ параллельна оси частот. Этот
наклон будет идти до сопрягающей частоты
.
Эта частота относится к апериодическому
звену Следовательно, наклон изменится
на -1. ЛАЧХ параллельна оси частот. Этот
наклон будет идти до сопрягающей частоты .
Так как это частота относится к
апериодическому звену, то наклон
изменится на -1. После частоты
.
Так как это частота относится к
апериодическому звену, то наклон
изменится на -1. После частоты наклон
изменится на -1и станет равным -2. Частота,
при которой частотная характеристика
пересечет ось частот, называется частотой
среза,
наклон
изменится на -1и станет равным -2. Частота,
при которой частотная характеристика
пересечет ось частот, называется частотой
среза,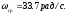
Фазочастотная характеристика (рис. 1.1, б) построена в соответствии с выражением

Значения
каждого из слагаемых определяются
приближенно для значений ω → 0, ω → ∞,
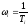 .
В этих точках
.
В этих точках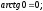
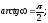
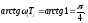
1.4 Уравнение состояния в нормальной форме,схема моделирования
Кроме входных и выходных переменных при описании систем выделяют переменные х, связанные с внутренней структурой устройства,- переменные состояния. Тогда систему можно описать с помощью уравнений состояния.
Нормальная форма уравнения состояния имеет вид:
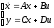 (1.3)
(1.3)
гдеА – матрица Фробениуса.
Матрица Фробениуса – это квадратная матрица, размер которой определяется порядком дифференциального уравнения. Элементы, стоящие над главной диагональю – единицы; элементы нижней строки - это коэффициенты левой части дифференциальногоуравнения, взятые с противоположным знаком, все остальные элементы – нулевые.
Согласно (1.2) дифференциальное уравнение системы имеет вид:


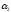
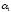
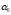

где
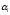 и
и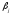 -
коэффициенты уравнения.
-
коэффициенты уравнения.

Для систем с одним входом и одним выходом D– одноэлементная матрица, В – вектор-столбец, состоящий из 3 элементов, которые определяются следующим образом:


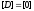 ;
;
Матрица С – вектор-строка, состоящая из 3 элементов, первый элемент единица, остальные нули:
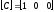 .
.
Подставим
рассчитанные матрицы в систему (1.3),
получим: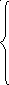

От матричной форме перейдем к скалярной:
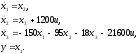

Схема модели приведена на рис.1.2:

Рисунок 1.2 – Схема модели, соответствующая уравнениям состояния в нормальной форме
