10

Интервал.

При преобразовании координат различные физические и геометрические величины, вообще говоря, изменяют свои численные значения. Это означает, что такие величины характеризуют не какое-либо объективное свойство точки, а лишь положение точки относительно конкретной системы координат.

В то же время, величины, сохраняющие свои численные значения при преобразованиях координат, отражают свойства самих изучаемых явлений и предметов и называются инвариантами преобразований.

Перед каждой теорией, в том числе и СТО, стоит задача отыскания таких величин (и законов).

Если в механике Ньютона такими величинами являлись расстояние между двумя точками и промежутки времени, то в релятивистской механике такая инвариантность утрачена.

В специальной теории относительности постулируется инвариантность скорости света в вакууме с. Другой инвариантной величиной в релятивистской механике является так называемый интервал между событиями 1 и 2, квадрат которого определяется как

(6.1)

где промежуток времени между событиями 1 и 2 и расстояние между точками, в которых происходят данные события, определенные в одной и той же системе отсчета ( ).

В инвариантности интервала легко убедиться, непосредственно вычислив его в и системах отсчета. Если координатные оси обеих систем ориентированы обычным образом и система движется относительно системы со скоростью в направлении оси , то из преобразований Лоренца следует

; ; ;

Тогда

.

Т.о., мы показали, что интервал действительно является величиной инвариантной относительно преобразований Лоренца, поэтому утверждение о том, что два события разделены некоторым интервалом , имеет абсолютный характер для всех инерциальных систем отсчета.

Для событий, происходящих на бесконечно малом удалении друг от друга, можем записать

. (6.2)

Инвариантность интервала является математическим выражением постоянства скорости света.

6.2. Пространство Минковского.

Немецкий ученый Г. Минковский (1864-1909) предложил геометрический метод описания пространственно-временных соотношений, в котором по правилам, определяемым преобразованиями Лоренца, каждому событию ставятся в соответствие три пространственных и одна временная координаты. Совокупность ( ) представляет собой мировую точку, характеризующую некоторое событие; всё многообразие мировых точек образует четырехмерное пространство, называемое пространством Минковского, или миром. Линия в пространстве Минковского - мировая линия. Каждой частице, даже неподвижной, в пространстве Минковского соответствует мировая линия.

Геометрия пространства Минковского определяется инвариантным относительно преобразований Лоренца расстоянием между двумя мировыми точками. Выражения (6.1) и (6.2) позволяют с формальной математической точки зрения рассматривать интервал как расстояние между двумя точками в воображаемом четырехмерном пространстве с координатами . В этом смысле интервал в четырехмерном пространстве Минковского аналогичен длине отрезка в «обычном» трехмерном пространстве в классической механике. Имеется, однако, существенное отличие: при образовании квадрата интервала квадраты разности координат по различным осям суммируются не с одинаковыми, а с различными знаками. Поэтому четырехмерную геометрию, определяемую квадратичной формой (6.2), называют псевдоевклидовой.

- радиус-вектор пространства-времени.

Совокупность координат события можно рассматривать как компоненты четырехмерного радиус-вектора в четырехмерном пространстве-времени. Поэтому -радиус-вектором пространства-времени называют совокупность четырех величин :

, (6.3)

или

, (6.4)

преобразующихся по определенному правилу:

; (6.5)

; (6.6а)

; (6.6в)

. (6.6с)

Примечание. Величины, снабженные верхним индексом, носят название контравариантных; нижним –

ковариантных.

Формулы полного преобразования Лоренца могут быть записаны в виде:

(6.7)

Если ввести матрицу преобразования , то:

(6.8)

где подразумевается суммирование по повторяющимся значкам, а сама матрица имеет вид:

(6.9)

Поэтому преобразования Лоренца представляются в виде:

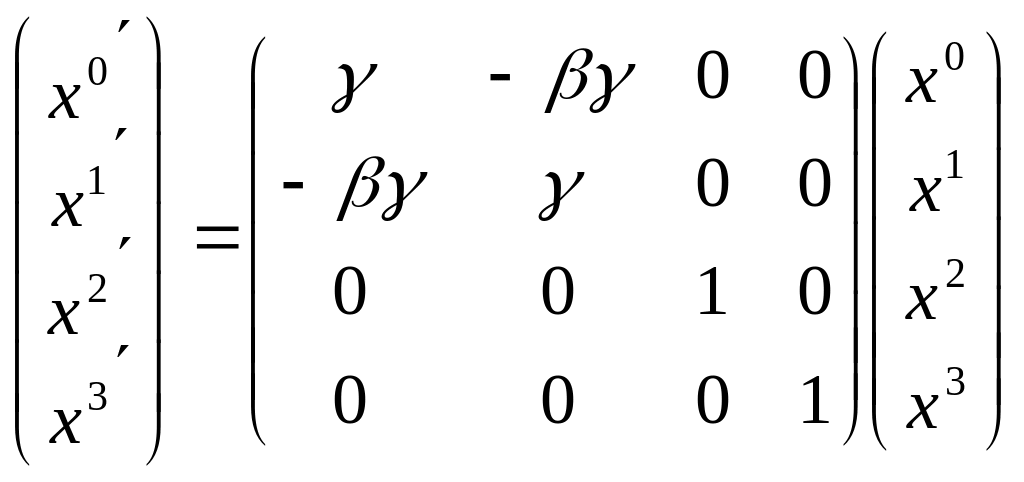(6.10)

Обратное преобразование:

(6.11)

Квадрат “длины” -радиус-вектора есть квадрат интервала, отсчитанный от начала системы отсчета:

. (6.12)

Совокупность четырех осей , имеющих общее начало, можно в широком смысле назвать системой координат.

Тогда формально преобразования Лоренца сводятся к повороту координатных осей – мерного пространства.

“Длина” – радиус-вектора при любых поворотах четырехмерной системы координат, в частности при преобразованиях Лоренца, всегда сохраняется.