Диференціальні рівняння 1

Диференціальні рівняння – рівність, яка містить незалежну змінну x, невідому функцію y та y^’..y⁽ⁿ⁾.

F(x,y,y^’..y⁽ⁿ⁾)

Порядок старшої похідної називається порядком даного рівняння.

Якщо невідома функція залежить від кількох змінних, то диференціальне рівняння називають диференціальним в частинних похідних, а якщо невідома функція залежить тільки від однієї змінної – звичайне диференціальне рівняння.

В теоріі диференціальних рівнянь в основному розглядаються диференціальні рівняння, що розв’язні відносно старшої похідної: y⁽ⁿ⁾=f(x,y,y^’..y^(n-1)). (1)

Функція y, що має неперервні похідні до n-го порядку включно, перетворює рівняння в тотожність – розв’язок рівняння. Графіком називають інтегральною кривою. Важливу роль в теоріі диференціальних рівнянь відіграє задача, яка полягає в знаходженні такого y=y(x), що задовільняє y(x₀)=y₀,y^’(x₀)=y^’₀, y^(n-1)(x₀)=y^(n-1)₀.

Перелічені умови називають початковими. n=1, y(x₀)=y₀ – означає, що серед усіх розв’язків диференціальних рівнянь треба знайти саме той розв’язок, графік якого проходить через точку (x₀,y₀).

Якщо розв’язок одержано у вигляді співвідношення φ(x,y)=0 (не розв’язане відносно y), таке співвідношення називають інтегралом (першим) диференціального рівняння.

Функція y=y(x,c₁..c_n), де c₁..c_n – довільні константи, називають загальним розв’язком рівняння (1), якщо ця функція є розв’язком рівняння (1) при довільному наборі констант.

Функція y=y(x) називається особливим розв’язком рівняння, якщо ця функція є розв’язком рівняння, але із загального розв’язку ії отримати ні при яких константах.

Звичайні диференціальні рівняння 1-го порядку

I. Диференціальні рівняння з відокремленими змінними

f₁(x)dx+f₂(y)dy=0

Інтегруючи це рівняння:

II. Диференціал рів-ня з відокремлюваними змінними

m(x)n(y)dx+m₁(x)n₁(y)dy=0 :(n(y)m₁(x))≠0

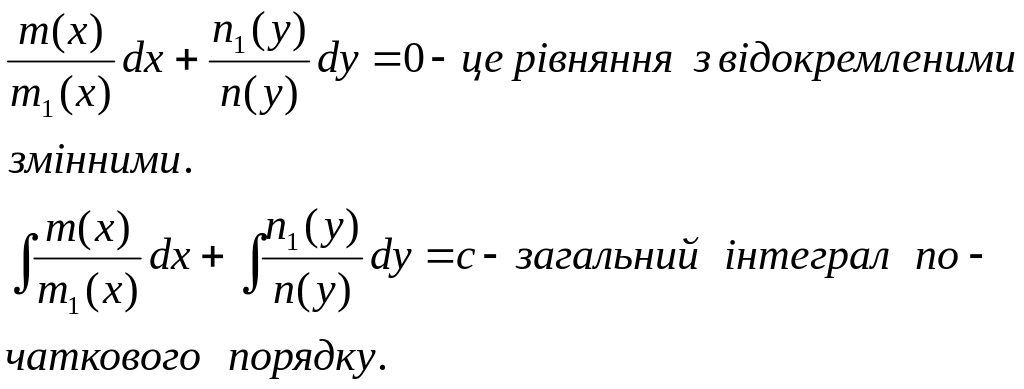
Значення n(y)=0, m₁(x)=0 треба перевірити додатково.

Ці значення x і y, якщо вони є розв’язком рівняння і не

містяться в загальному розв’язку, є особливим

розв’язком рівняння.

III. Диференціальні рівняння, що приводяться до рівнянь з відокремлюваними змінними

1. y^’=f(ax+by+c) приводиться до рівняння з

відокремлюваними змінними за допомогою

підстановки ax+by+c=z, де z – нова функція.

Диференціюючи, маємо:

a+by=z^’

Підставивши замість y та y^’ іх значення в початкове

рівняння:

2. До диференціальних рівнянь з відокремлюваними

змінними відносяться рівняння виду: IV. Однорідні диференціальні рівняння.

f(x,y) – однорідна, якщо для будь-якого t

f(tx,ty)=t^kf(x,y), де k – степінь однорідності. Однорідні диференціальні рівняння приводяться

до рівнянь з відокремлюваними змінними

за допомогою підстановки: y/x=z, y=zx, y^’=z^’x+z. z^’x+z=

f(z). Останнє рівняння є диференціальним з

відокремлюваними змінними. Відокремлюючи змінні,

маємо:

V. Диф. Рівняння, які приводяться до однорідних. 2

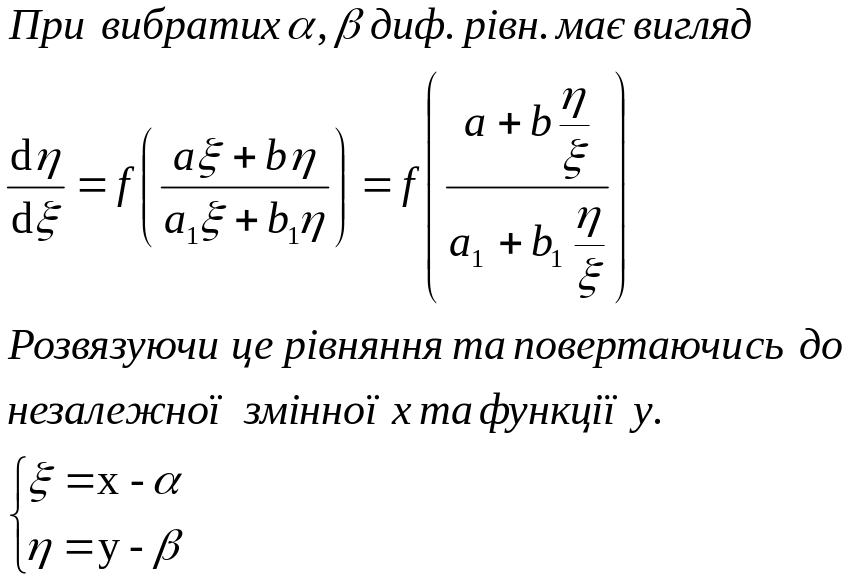
Одержимо занальний інтеграл початкового рівня.

VI. Лінійні диф. Рівняння 1-ого порядку

2).Метод підстановки

Суть метода в слідуючому: розвязок лініного, неоднорідного диф. рівняння

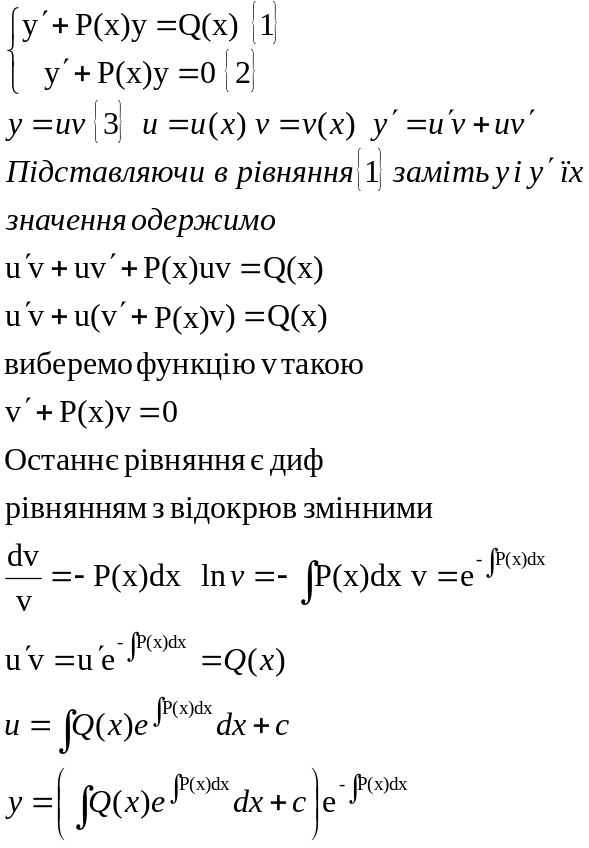
VII. Диф. р-ня Бернуллі 3

Зауважимо: якщо n=0, то дане р-ня перетворюється в лінійне, а при n=1, то в р-ня з відокремлюваними змінними.

Існує два методи інтегрування диф. р-нь Бернуллі:

1) Метод зведення диф. р-нь Бернуллі до лінійного.

Розділемо все р-ня на уⁿ :

Диференцюючи це р-ня маємо:

Підставимо замість у і у’:

Останнє р-ня є лінійним. Інтегруючи його та повертаючись до старої ф-ції у за доп. заміни у^1-n=z – одержемо загальний інтеграл р-ня.

2) Метод підстановки інтегрування диф. р-ня Бернулі

Підставляючи замість у і у’ їх значення в початкове р-ня:

Виберемо ф-цію v таку, щоб

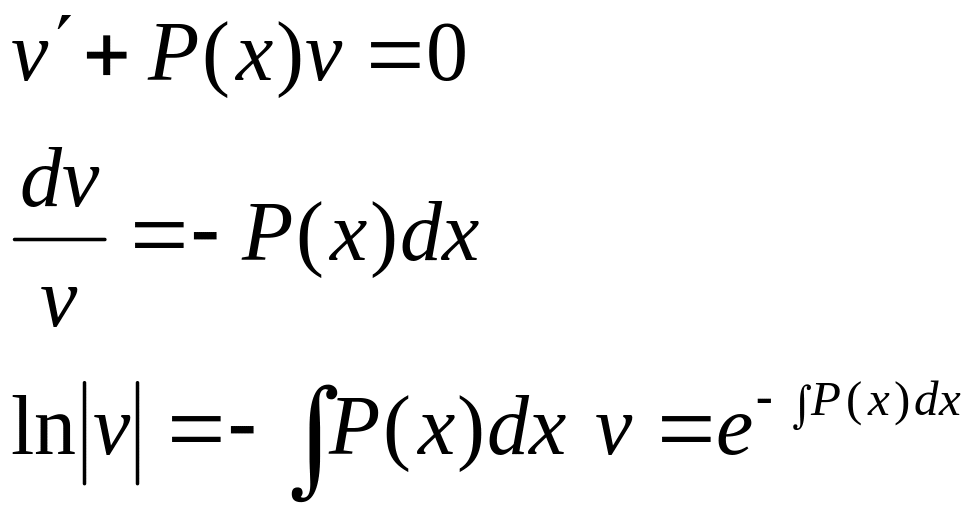
Підставляючи замість v його значення в диф. р-ня:

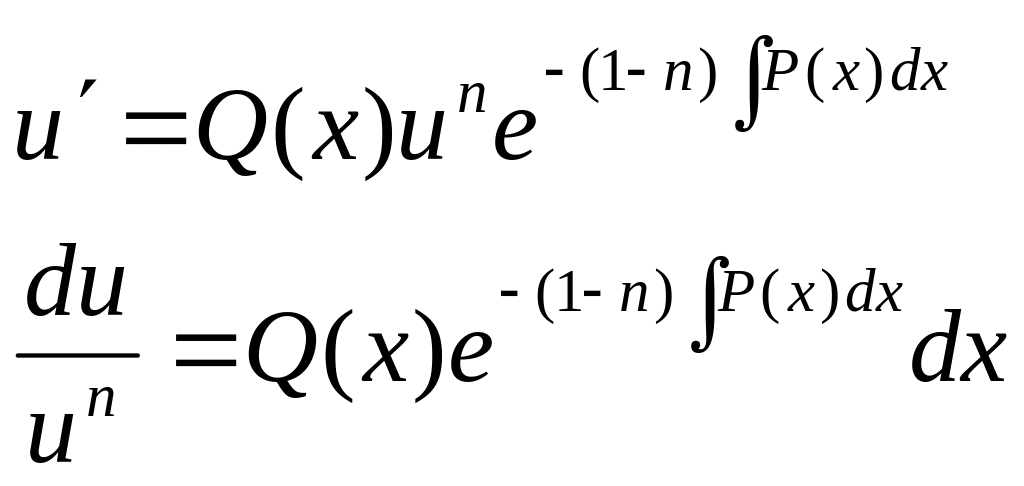
Інтегруючи останнє р-ня знайдемо ф-цію u, а розв’язком буде добуток ф-цій u*v

VIII. Диф. Р-ня в повних диференціалах

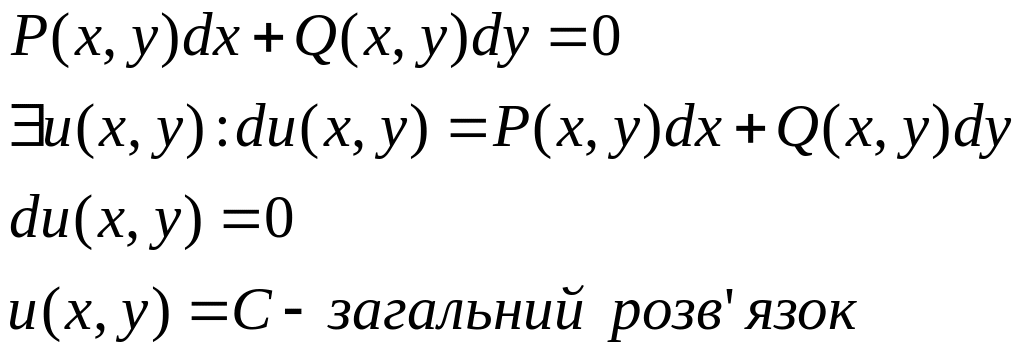
Із теореми про незалежність криволінійного інтегралу від шляху інтегрування маємо, що ліва частина диф. р-ня буде повним диференціалом ф-ції u(x,y) тоді, коли

Розглянемо один з методів знаходження ф-ції u(x,y)

1)

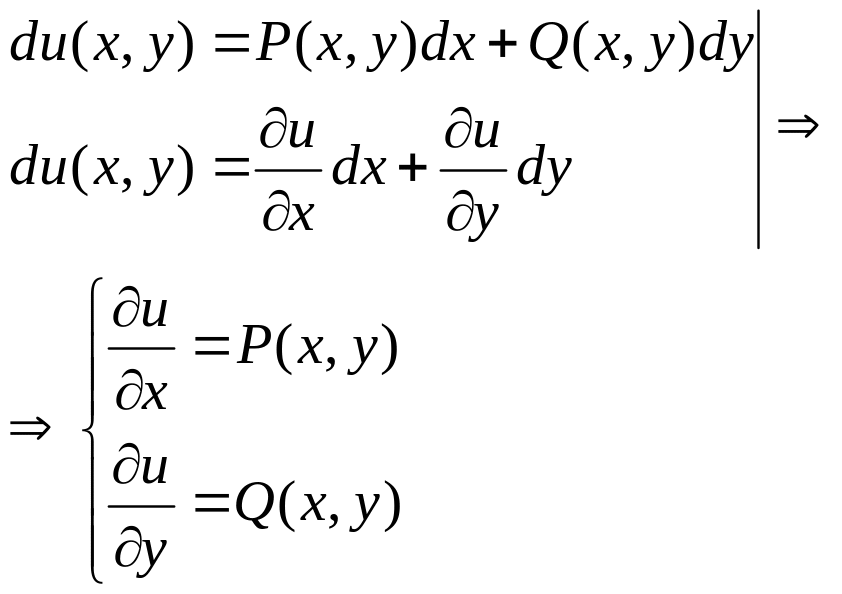
Інтегруючи довільне з цих р-нь, наприклад перше маємо:

Щоб знайти ф-цію С(у), то використовуємо ін. умову

Із останнього р-ня знаходимо С’(у), а потім і саму ф-цію С(у)

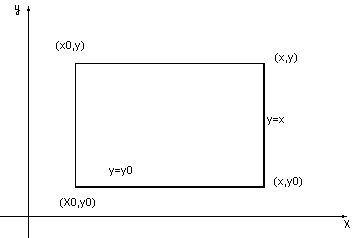
2) P(x,y)dx+Q(x,y)dy=0 – р-ня повних диференціалів, тоді за теоремою про незалежність криволінійного інтегралу від шляху інтегрування будемо мати, що фіксуючи деяку точку (x₀,y₀) і беручи точку (х,у) будемо інтегрувати по осям

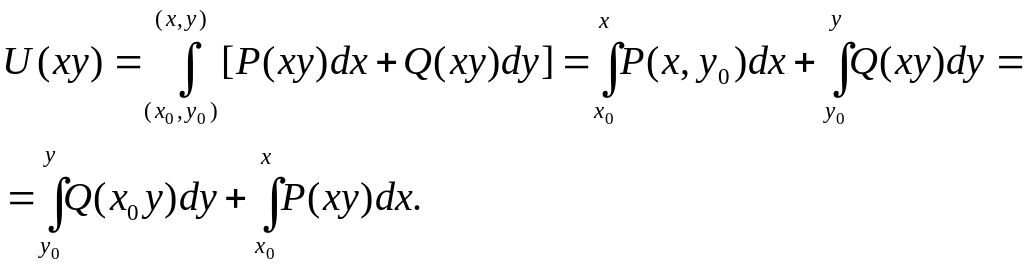
Інтегрувальний множник 4

Припустимо, що P(xy)dx+Q(xy)dy=0 не є рівнянням в повних диференціалах, тобто

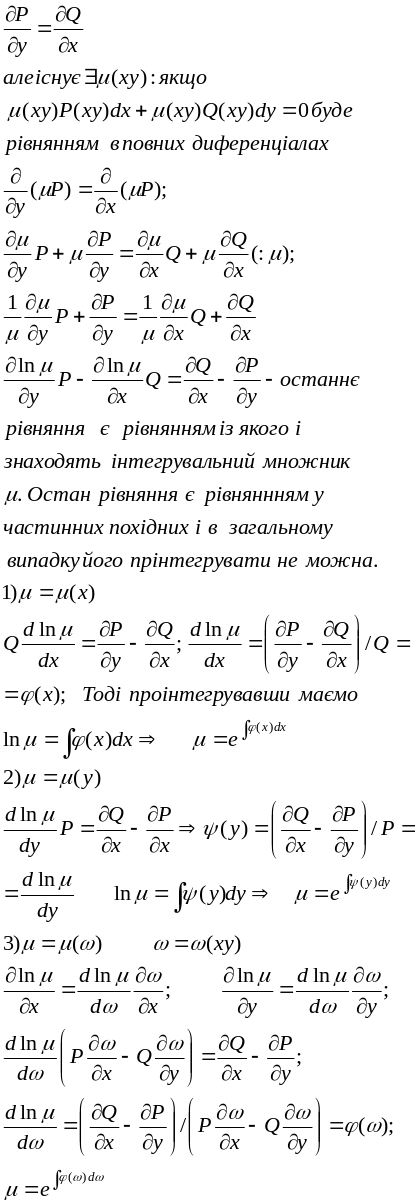Диференц. Рівняння які не є диференціальними рівняннями в повних диференціалах можна інтегрувати за допомогою метода виділення повного диференціалу при цьому слід приміняти формули для обчислення диференціалу функції

dCx)=Cdx

dxy)=ydx+xdy

d(x/y)=(ydx-xdy)/y²

d(e^y)=e^ydy

d(x²+y²)=2xdy+2ydx.

Диференціальні рів-ня I-го порядку, не розв’язані відносно похідної

I. Диференціальні рівняння І порядку, які можна розв’язати відносно похідної.

Припустимо, що диференціальне рівняння , можна розв’язати відносно похідної, тоді одержимо одне або кілька рівнянь розв’язаних відносно похідної. одержимо загальний інтеграл цього рівняння

Загальний інтеграл цього рівн. записується у вигляді:

ІІ. - рівн. не містить x і y, а тільки похідну. Припустимо, що - є розв’язок рівн. , тоді

Підставляючи замість a, його значення в загальний розв’язок, маємо:

ІІІ. Рівняння, які не містять невідомої функції.

Припустимо, що це рівняння припускає параметризацію.

IV. немає x

Припустимо, що рівн. припускає параметризацію:

- загальний розв’язок цього рівняння.

Диференціальні рівняння Лагранжа 5

Диф. рівн. Лагранжа наз. рівн.

За допомогою введення параметра

Покладемо:

- останнє рівняння є лінійним рівнянням.

Припустимо, що його загальний розв’язок - розв’язок рівняння Лагранжа в параметричному вигляді.

Диференціальне рівняння Клеро

Диф. рівн. Клеро наз. рівн. виду , це той випадок рівн. Лагранжа, коли

Рівн. Клеро, як і рівн. Лагранжа будемо розв’язувати за допомогою метода введення параметра.

Покладемо:

- заг. розв’язок рівн. Клеро.

Лінійні диф. рівняння n-го порядку

x-невідома змінна;

у-невідома функція;

P₁(x),P₂(x),..,P_n(x)-задані неперервні функції від х;

f(x)- неперервна функція змінної х;

Якщо f(x)=0 хєХ, то рівняння набуває вигляду:

Лінійним однорідним диф. рів. n-го порядку яке відповідає лінійному неоднорідному диф. рів. (1);

Позначемо ліву частину рівн. (1) і (2) через:

L(y)-

наз. лінійним диференіальним оператором.

Властивості лінійного диф. оператора:

1) Дов.С=const L(Сy)=CL(y)

дійсно 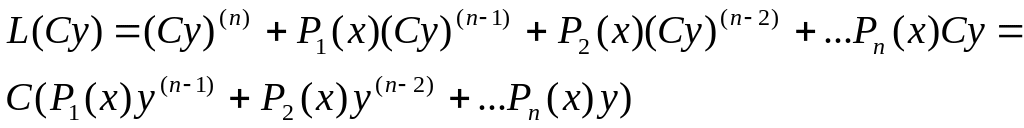2)

доведення

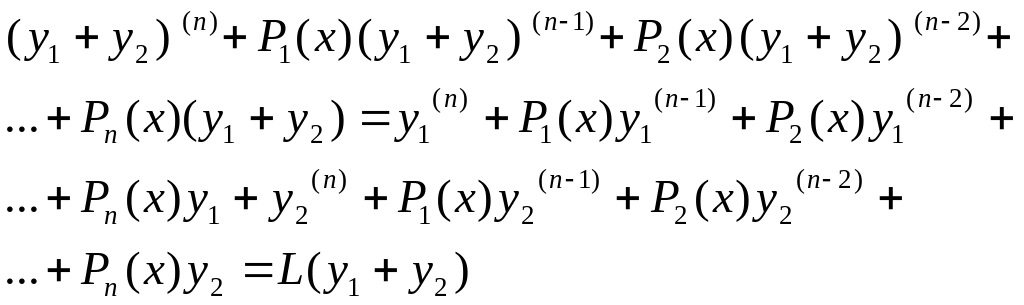
Висновок: для дов. Const C₁ C₂…C_n

Властивості розв’язків лінійного неоднорідного диф. рів. n-го порядку.

Нехай маємо лінійне диф. рів. n-го порядку (2) та не лінійне (1);

1). якщо то для дов. С=const доведення

є роз. рів. (2) то L(y₁)=0 розглянемо L(Cy₁)=CL(y₁)=0 а це і озн. що сума Су₁(х) є розв’язком рівняння (2)

Ч.т.д

2) y₁=y₁(x) y₂=y₂(x) розв. (1), то їх сума та різниця у₁+у₂ теж є рівняння (2); доведення

оскільки у₁-є розв’язок (2) то L(y₁)=0, L(y₂)=0

L(y₁+y₂)=L(y₁)+L(y₂)=0 => y₁+y₂ є розв. (2);

Висновок: якщо y₁=y₁(x) y₂=y₂(x) є розв. (2) то якими б не були дов. C=const i=1,n;

теж буде розв’язки рівн.(2)

3) Якщо комплексна ф-ція U(x)+iV(x) є розв’язком (2) то дійсна частина U(x) і уявна частина V(x) теж є розв. (2);

доведення

U(x)+iV(x) –розв.(2) L(U+iV)=0 Використовуючи вл-сті:

L(U)+iL(V)=0

Відомо що комплексне число =0 тоді і тільки тоді, коли 0 дорівнює і дійсна частина:

Диф рівняння вищіх порядків 6

І. Диф. рівн. вищіх порядків, які припускають зниження порядку.

Одержимо його загальний

ІІ. До другого типу диф. рівн., які припускають зниження порядку відносно рівн. виду:

Це рівн. не містить невідомої ф. y, та похідних цієї ф. до (k-1) порядку включно.

Порядок цього рівн. можна знизити на k одиниць, за допомогою підстановки:

, підставляючи в диф. рівн. замість похідних ф. їх значення, отримаємо , припустимо, що останнє рівн. можна проінтегрувати, припустимо, що - його загальний розв’язок.

Інтегруючи це рівн. k-разів, одержимо загальний розв’язок початкового рівн.

ІІІ Диф. рівняння які не містять незалежної змінної:

порядок цього рівняння можна знизити за допомогою підстановки z=y’, де z=z(y)=>y(x), то z- складена функція від x. z=z(x);

Аналогічно знаходяться похідні вищих порядків. Підставляючи в диф. рівн. замість похідних від функції їх значення одержимо диф. рівняння (n-1) порядку. Припустимо що одержане диф рівняння можна проінтегрувати і нехай

повертаючись до старої функції у

Останнє рівняння є диф рівн. з відокремлювальними змінними

Інтегруючи останнє рівняння одержимо загальний інтеграл початкового рівн.

ІV. Однорідні диф. рів. вищих порядків:

- наз. однорідною відносно невідомої ф-ції y та її похідних якщо дов. t (const, або змінна).

Число к- степінь однорідності однорідні диф. рів. вищих порядків інтегруються за допомогою підстановки:

- де z нова невідома функція

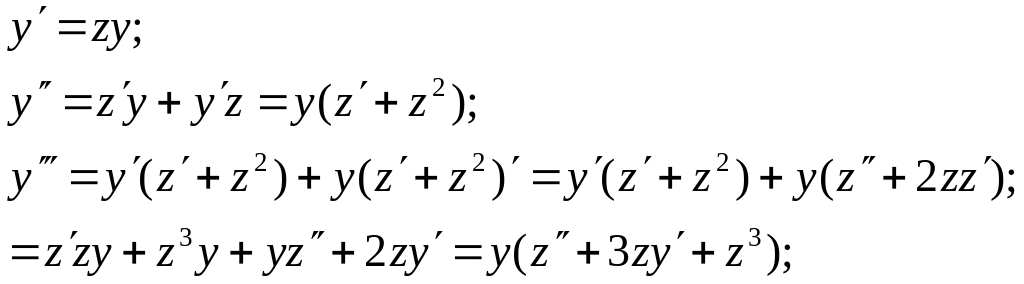Аналогічно обчислюються похідні вищих порядків Підставляючи в диф. рівн. замість похідних від функції z їх значення одержимо диф. рівняння (n-1) порядку. Припустимо що одержане диф рівняння можна проінтегрувати і нехай Повертаючись до старої невідомої функції у

Інтегруючи останнє рівняння:

V. Диф. рів. ліва частина яких є точною похідною деякої функції:

останнє рівняння є диф. рів. (n-1)- порядку інтегруючи це рівняння одержимо загальний його інтеграл.

Лінійно залежні та лінійно незалежні розв’язки 7 лінійного однорідного диф. рів-ня

розв.(2) y₁=y₁(x)…y₂=y₂(x) наз. лінійнозалежними на відрізку [a,b], якщо існують const.

із яких хоч би одна відмінна від 0, такі що виконувалась рівність:

Припустимо _n не равно 0

Вираз, який стоїть в правій частині останньої рівності наз. лінійною комбінацією ф-цій у₁(x), у₂(x) і т.д. у_n-1(x);

Функції у₁(x), у₂(x) і т.д. у_n-1(x) наз. лінійною залежна на відрізку [a,b] якщо хоч би одна із ф-цій є лінійно залежною.

Функції у₁(x), у₂(x) і т.д. у_n-1(x); наз. лінійною незалежна на відрізку [a,b] якщо

якщо рівність виконується тільки ₁=₂=…=_n=0

1) 1,x,x²,…,xⁿ –лінійно залежні на відр.[a,b]

на дов. [a,b] числової прямої. Розглянемо дов. комбінацію цих функцій

Останнє рівняння є рів. n-го степеня. а тому воно може мати не більше ніж n коренів, а значить перетворюється в 0 не більше ніж в n точках, а значить в кожній точці відрізка [a,b] ця рівність виконуватися не може. Покажемо що

2). є лінійно незалежною

к₁ <>к₁<>…<>k_n. на дов. [a,b], дов. будемо доводити від супротивного.

Доведення

Припустимо є лінійно залежною

к₁ <>к₁<>…<>k_n. на дов. [a,b], тоді за озн. лінійної залежності ф-цій маємо що існують const

із яких хоч би одна не дорів. 0 такі що

Розділемо останнє рівняння на одерж.

Продиференціюємо останню рівність по х:

Поділемо на :

Продиф останю нерівність:

Продовжуючи цей процес одержимо після n-го кроку слідуючу тотожність

Одержана суперечність і доводить цю властивість

3). Якщо у₁,у₂,…у_n, лінійно залежні розв’язки рівн. (2) то визначник Вронського цієї системи

W(x)=0 для дов. xє[a,b].

Оскільки ф-цій у₁,у₂,…у_n, є лінійно залежними розв’язками рівн. (2), то за озн. лінійної залежності сист. функцій, маємо хоч би одне із цих функцій є лінійною комбінацією інших.

Припустимо:

Підставляючи замість y_n та похідних цієї функції їх значення в визначник вронського маємо:

Одержаний визначник =0 тому що останній стовбець визн. є лінійною залежністю інших стовбців.

4). Теорма про загальний розв’язок лінійного однорідного диф. рівняння n-го порядку:

у₁,у₂,…у_n- лінійно незалежні розв. рівняння.(2)

то загальний розв’язок рівн.(2) має вигляд

де С₁,С₂,…,С_n,- дов. константи є загальними розв’язками (2);

Доведення

y_i=y_i(x) i=1,n розв.(2) =>

Підставляємо замість

в диф. рівняння (2)

Останнє рівняння озн. що функція y є розв’язком лінійного одн. рівняння (2) Оскільки це функція містить n-дов const то вона є загальним розв’язком цього рівняння.

Визначник Вронського

Нехай маємо лінійне однорідне диф. рів. (2) і нехай у₁,у₂,…,у_n – розв’язки цього рівняння

Розглянемо визначник:

цей визначник наз визначником Вронського

Лінійні однорідні диф. рівняння зі сталими 8 коефіцієнтами

а_і=Const для дов і=1,n

Розв’язок ріняння (2) будемо шукати у=e^kx (3)

Підставляючи в (2) замість у і похідні від у їх значення одержимо слідуючу тотожність

(4)

характеристичне рівняння (2)

Характерестичним рів. записуетья зразу по виду диф. рівн., замінюючи тільки похідні від функції у відповідні степені к.

Оскільки х-тичне рівн.(4) є алгебраїчним рівн. n-го степеня то воно має n-коренів

Можливі випадки:

ці функції є лінійно незалежними на відрізку [a,b], а тому загальним розв’зком рів.(2)

2).Серед коренів хар-ного рівня є корені комплексні:

k₁=a+ib k₂=a-ib y₁=e^(a+ib)x=e^ax(cosbx+isinbx)

За 3 властив. розв’язків лінійного диф рів-ня маємо,що:

y₁¹=e^axcosbx y₁²=e^axsinbx

Ці розв’язки лінійно незалежні.

k₂=a-ib y₂’= e^axcosbx

y₂’’= -e^axsinbx – лінійно залежні з y₁¹ та y₁²

y=e^ax(C1cosbx+C2sinbx)

3).Серед коренів хар-ного рів-ня є корені кратні:

k₁= k₂=……..= k_n

Часткові розв’язки диф. рів-ня 2:

y₁=e^k1x y₂=xe^k1x y₃=x²e^k1x y_m=x^m-1e^k1x

y=e^k1x(C1+C2x+…Cmx^m-1)

Якщо кратними є комплексні корені:

k₁= k₂=a+ib k₃= k₄=a-ib

y=e^ax((C1+C2x)cosbx+(C3+C4x)sinbx)

Лінійні неоднорідні диференціальні рівняння n-го порядку

Має вигляд: y⁽ⁿ⁾+P₁(x)y^(n-1)+..+P_n(x)y=f(x) (1)

y⁽ⁿ⁾+P₁(x)y^(n-1)+..+P_n(x)y=0 (2)

L(y)=f(x) (1’)

L(y)=0 (2’)

Теорема 1: y=y₁(x) - розв’язок (2) =>

y=y₂(x) – розв’язок (1)

=> y₁(x)⁺_-y₂(x)

Оскільки

y=y₁(x) - розв’язок (2) => L(y₁)=0

y=y₂(x) – розв’язок (1) => L(y₂)=f(x)

L(y₁⁺_-y₂)=L(y₁)⁺_-L(y₂)=f(x) => y₁⁺_-y₂

Теорема 2 (теорема про загальний розв’язок лінійного

неоднорідного диференціального рівняння n-го

порядку): Якщо y₀ – загальний розв’язок (2),

y_ч - частинний розв’язок (1), тоді y=y₀+y_ч.

Доведення: Оскільки y₀ – загальний розв’язок (2), то

він є лінійною комбінацією n часткових розв’язків

(2). Оскільки y_ч – частинний розв’язок рівняння (1),

то за вищедоведеною теоремою y=y₀+y_ч

Лінійні неоднорідні диференціальні рівняння зі сталими коефіцієнтами

y⁽ⁿ⁾+a₁y^(n-1)+..+a_ny=f(x) (1)

y⁽ⁿ⁾+a₁y^(n-1)+..+a_ny=0 (2)

Частинний розв’язок рівняння (1) можна знайти у двох випадках:

1) f(x)=P_m(x)e^ax, де P_m – многочлен m-го степеня, a - деяка

константа.

y_m=Q_m(x)e^axx^k, де Q_m(x) – многочлен степеня m з

невідомими коефіціентами. k - число коренів

характеристичного рівняння, рівних a.

Щоб знайти невідомі коефіцієнти многочлена Q_m(x),

треба в рівняння (1) підставити значення функціі y та

ії похідних. Одержану після цього тотжність скороти-

ти на e^ax і після цього прирівняти коефіцієнти при од-

накових степенях x в лівій і правій частинах. Із одер-

жаної системи знаходимо невідомі коефіцієнти.

2) f(x)=e^ax(P₁(x)cosbx+P₂(x)sinbx)

a і b – деякі константи. P₁(x) і P₂(x) – задані

многочлени, причому один з них може дорівнювати 0.

y₂=e^ax(Q₁(x)cosbx+Q₂(x)sinbx)x^k, де Q₁(x) і Q₂(x) - мно-

гочлени одного степеня з невизначеними коефіцієн-

тами. Степінь цих многочленів дорівнює вищому із

степеней многочленів P₁(x) та P₂(x). Число k дорівнює

числу коренів характеристичного рівняння, рівний чис-

лу a+ib. Невизначені коефіцієнти многочленів Q₁(x) і

Q₂(x) знаходяться за допомогою метода невизначених

коефіцієнтів. Суть його у слідуючому:

в початкове дифренціальне рівняння замість y

підставляємо y_ч, одержимо тотожність, скоротимо на

e^ax. Після цього прирівнюємо коефіцієнти при cosbx та

sinbx в обох частинах. Потім в одержаній тотожності

прирівнюємокоефіцієнти при однакових степенях x. В

результаті одержимо систему лінійних рівнянь, із якої

і знаходимо всі невизначені коефіцієнти.

Метод варіації довільних сталих при інтегруванні 9 лінійного однорідного диф. рів-ня n-го порядку

Нехай маємо :

Припускаємо, що заг розв’язок (2):

Заг розв’язок р-ня (1) будемо шукати у точно такому вигляді як розв р-ня (2). Тільки замість констант виб ф-ї:

Знайдемо похідну від у

Виберемо ф-ї такими щоб сума

Знайдемо похідну другого порядку від у

Знову виберемо ф-ї С_К (х) такими щоб таким чином отримаємо:

Підставимо у (1) значення у та його похідних їх значення

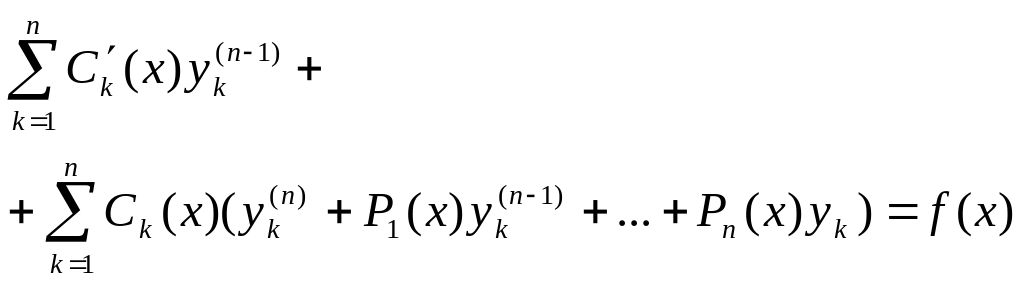
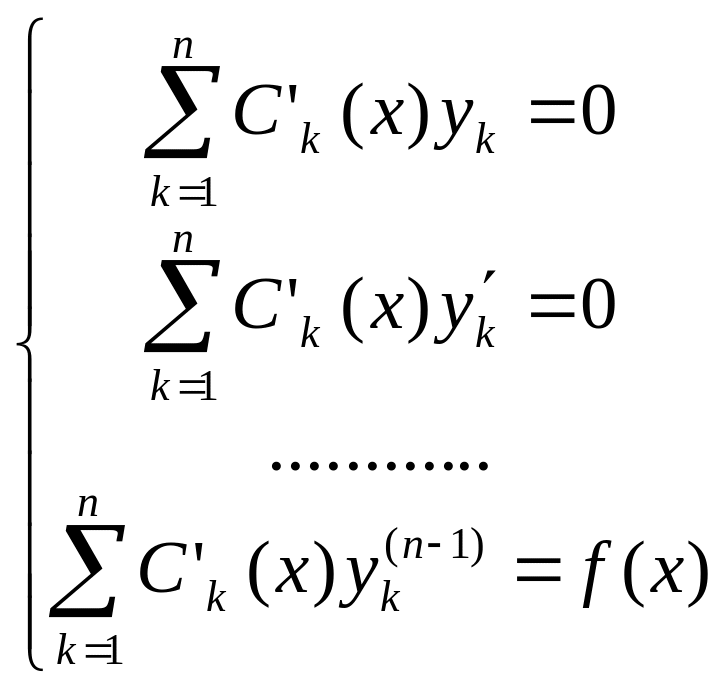
Оскільки основний визначник цієї системи є визначником Вронського, лінійно незал розв’язків ЛОДР n-го порядку, а тому цей визначник відмінний від 0 і тому ця система має єдиний розв’язок нехай - розв’язки даної сист.

Підставляючи маємо:

Диференціальні рів-ня Ейлера

р-ня виду:

ДРЕ приводиться до ЛДР n-го порядку зі сталими коеф за доп підстановки х=е^t у=у(х)=у(t).

Викор ф-лу для обчисл похідної від ф-ї заданої парам р-ми маємо:

Продовжуючи знаходити похідні та підставляючи їх одержимо ЛДР зі сталими коеф.

Інтегруючи та повертаючись до старої змінної Х одержимо заг розв ДРЕ.

Зауважимо, що для ДР виду Викор підстановка ах+b=е^t.

Системи звичайних диференціальних рівнянь 10

система виду:

Х – незал змінні. У – невідомі ф-ї. F – задані ф-ї своїх аргументів.

Якщо цю систему можна розв’язати відносно похідних то система набуває виду:

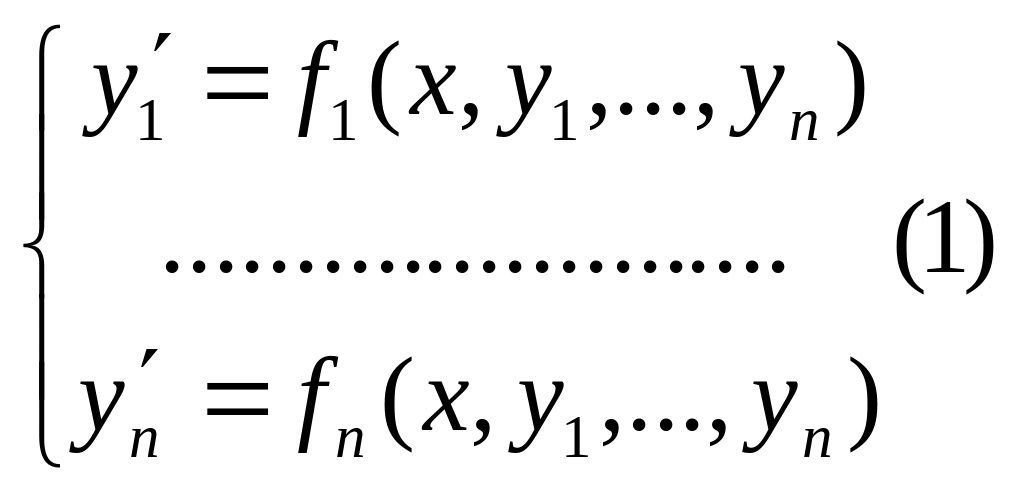
(1)- нормальна система звич ДР. У₁=У₁(Х), .... , У_n=У_n(Х) – розв’язки системи (1)

- заг розв’язок сист (1) при умовах:

– при дов наборі С₁,...,С_n ф-ї У₁, .... , У_n – розв (2)

– к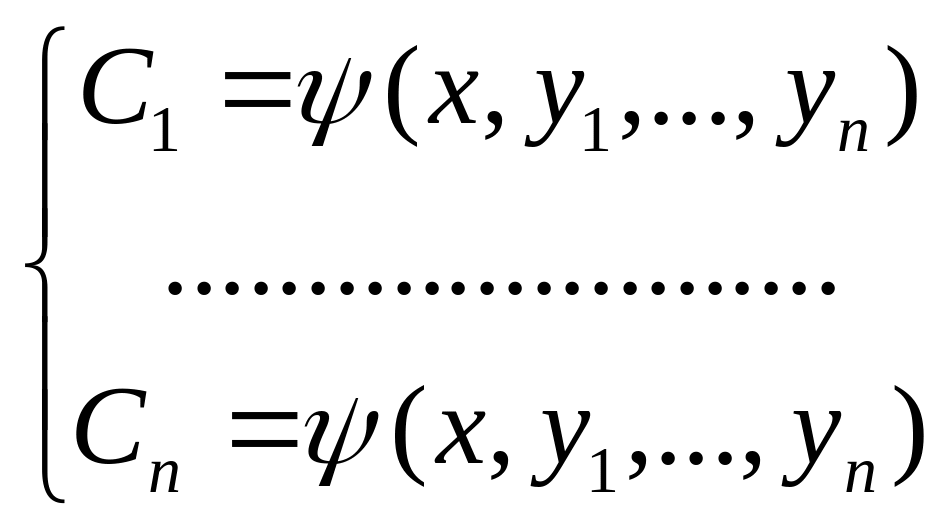 ожне із рівнянь наз 1-м інтегралом даної системи

Розв сист це значить знайти n незал перших її інтегралів.

Системи диф. рівнянь в симетричній формі

Називають у вигляді нормальної

Вірне також і обернен твердження, якщо система записана у вигляді нормальної, її можна записати у вигляді системи в симетричній формі

Основні методи інтегрування звичайних диф. рівнянь

I. Метод зведення системи до 1 рв

Суть методу: одне із рівняь диференціюємо (n-1) раз після кожного разу підставляємо в систему значення похідних. Із першого рівняння та одержаних (n-1) рівнянь вилучемо всі невідомі функції через у₁ і підставимо ці значення в одержане вище рівняння. Інтегруючи, знайдемо невідому у₁. Всі інші невідомі функції знаходяться операцією диференціювання.

II. Метод інтегровних комбінацій

Інтегровні комбінації – це легкоінтегровне диференціальне рівняння.

Щоб одержати загальний розв’язок бажано систему записати в симетричній формі і знайти для неї (n-1) незалежних перших інтегралів. Для знаходження використовують метод інтегрованих комбінацій. Для побудови інтегровних комбінацій широко використовують слідуючи властивість:

має місце

насправді:

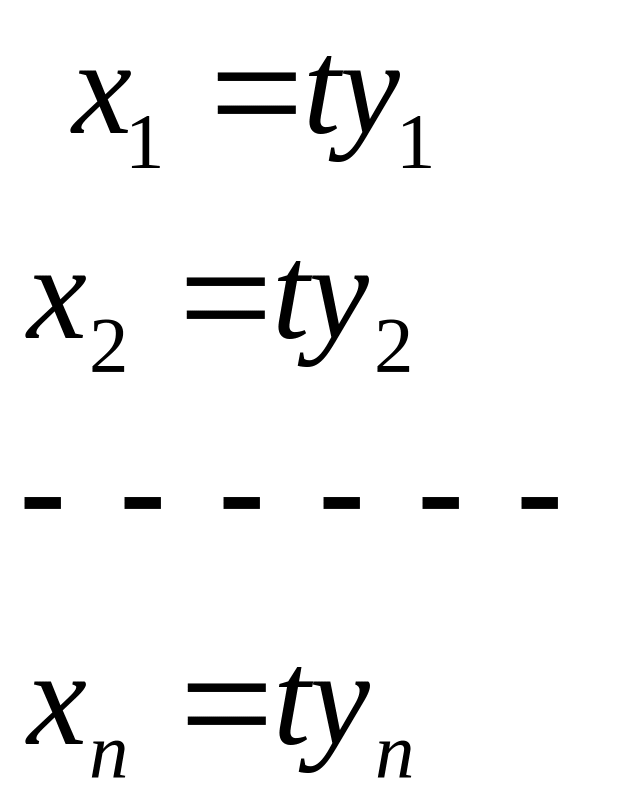
1).Диференціальні рівняння

Звичайні диференціальні рівняння 1-го порядку

Диференціальні рівняння з відокремленими змінними

Диференціал рів-ня з відокремлюваними змінними

Диференціальні рівняння, що приводяться до рівнянь з відокремлюваними змінними

Однорідні диференціальні рівняння

2).Диф. рівняння, які приводяться до однорідних

Лінійні диф. рівняння 1-ого порядку:

Метод варіації довільної сталої

Метод підстановки

3).Диф. р-ня Бернуллі

Диф. р-ня в повних диференціалах

4).Інтегрувальний множник

Диференціальні рів-ня I-го порядку, не розв’язані відносно похідної

5).Диференціальні рівняння Лагранжа

Диференціальне рівняння Клеро

Лінійні диф. рівняння n-го порядку

Властивості лінійного диф. оператора

Властивості розв’язків лінійного неоднорідного диф. рівняння n-го порядку

6).Диф рівняння вищіх порядків:

які припускають зниження порядку

які не містять незалежної змінної

однорідні

ліва частина яких є точною похідною деякої функції

7)Лінійно залежні та лінійно незалежні розв’язки лінійного однорідного диф. рів-ня

Теорма про загальний розв’язок лінійного однорідного диф. рівняння n-го порядку

Визначник Вронського

8)Лінійні однорідні диф. рівняння зі сталими коефіцієнтами

Лінійні неоднорідні диференціальні рівняння n-го порядку

Лінійні неоднорідні диференціальні рівняння зі сталими коефіцієнтами

9).Метод варіації довільних сталих при інтегруванні лінійного однорідного диф. рів-ня n-го порядку

Диференціальні рів-ня Ейлера

10).Системи звичайних диференціальних рівнянь

Системи диф. рівнянь в симетричній формі

Основні методи інтегрування звичайних диф. рівнянь