Первісна

Припустимо, що f(x) х є Х задачею диферент. числення є знаходження похідної від f(x) – f’(x). Задачею інтегрального числення є обернена до задачі диф. числення, тобто знаючи похідну треба знайти саму ф-цію.

Ф-ція F(x) х є Х наз. первісною для ф-ції f(x) х є Х, якщо

Зауважимо, якщо F(x) є первісною для f(x) х є Х (F’(x)=f(x)), то С=const (F(x)+C)’= f(x)

Якщо f(x) і g(x) мають однакові первісні, то

f(x)- g(x)=С

Невизначеним інтегралом від ф-ції f(x) наз. сукупність всіх первісних для ф-ції f(x). Якщо F’(x)=f(x), то невизначений інтеграл:

Властивості невизначених інтегралів

1)

Доведення: Нехай F’(x)=f(x), тоді

Розглянемо:

2)

3)

Доведення: F’(x)=f(x), тоді

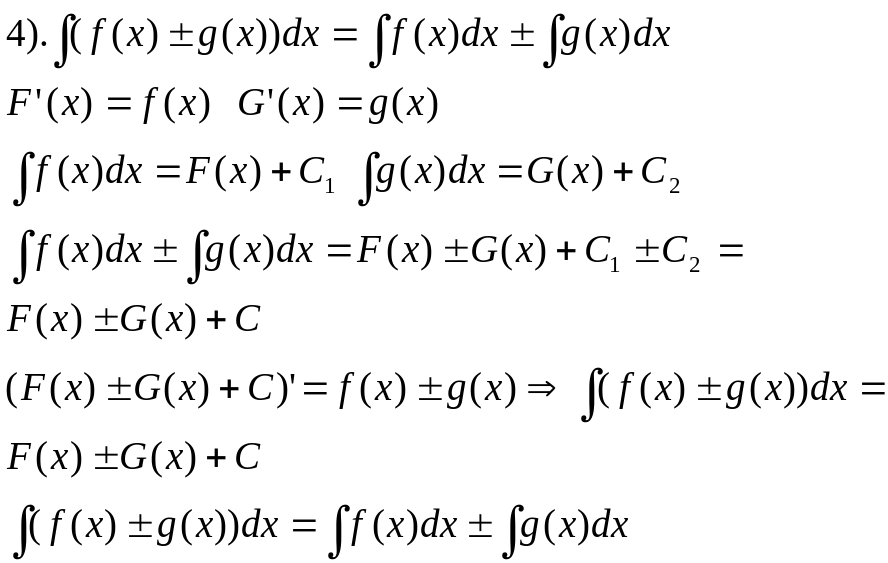
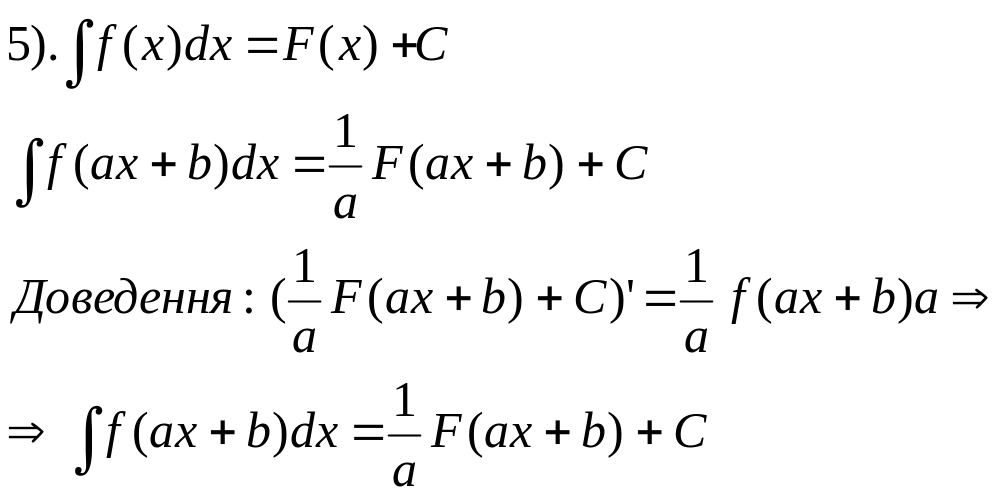
Основні методи обчислення невизначених інтегралів.

1.Метод безпосереднього обчислення невизначених інтегралів.Цей метод грунтується на властивостях невизначених інтегралів та таблиці невизначених інтегралів.

2.Метод заміни змінної. Метод підстановки.

тоді

Доведення: Розглянемо похідну

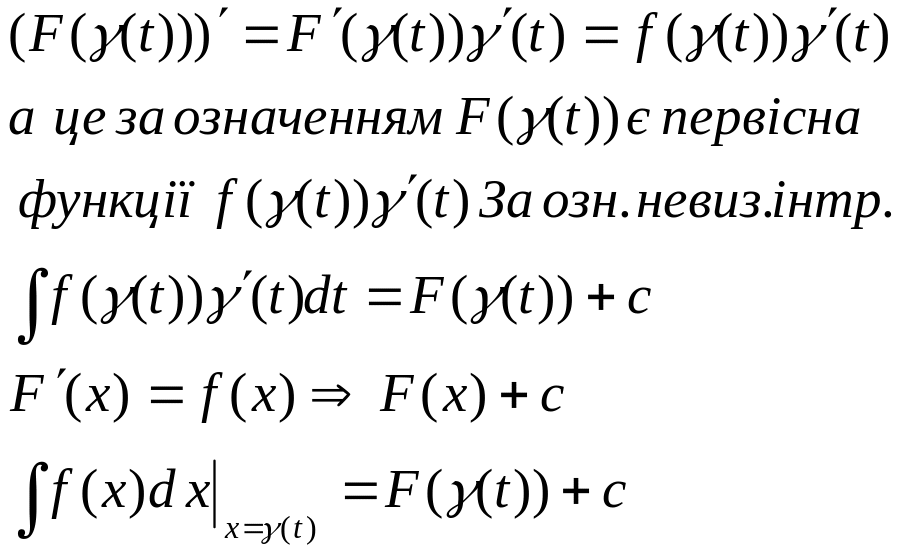
Оскільки праві частини останніх двох рівностей однакові, то й ліві однакові.

3.Метод інтегрування частинами

u=u(x) v=v(x) мають похідні, які неперер. На множ. Х , тоді

Зауважимо, що формула інтегрування частинами в основному викор. для інтегр. Функцій різних класів.

З цих дві останні завжди через u. При добутку степеневої на показникову або тригонометричну, то степенева через u. При добутку показникової на тригонометричну різниці немає.

Рекурентна формула

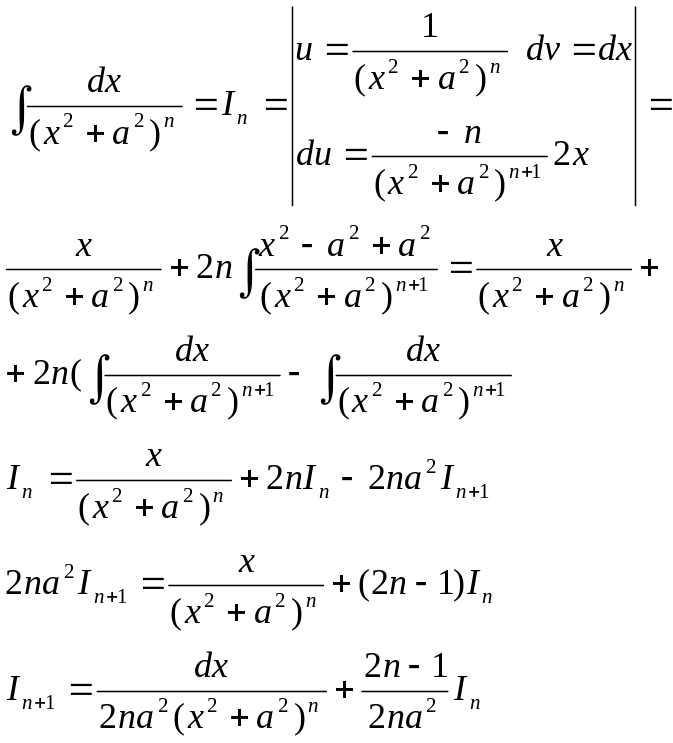
Комплексні числа

Комплексне число ,число виду Z=X+iY, де I = ,Х- дійсна частина, Y –уявна частина. =X-iY назив. спряжений до комплексного числа Z . Z* = (X+iY)(X-iY)=X²-i ²Y²=X²+Y².

Геометрична інтерпретація: М є зображенням комплексного числа на площині XOY а це і означає що комплексні числа на площині. Іноді комплексні числа трактують як радіус-вектор точ. М.Якщо уявна частина Y=0, то Z=X дійсне число. Якщо дійсна частина X=0, то Z=iy.

Тригонометрична форма комплексного числа

Z=x+iy, |OM|-модуль компл. числа. 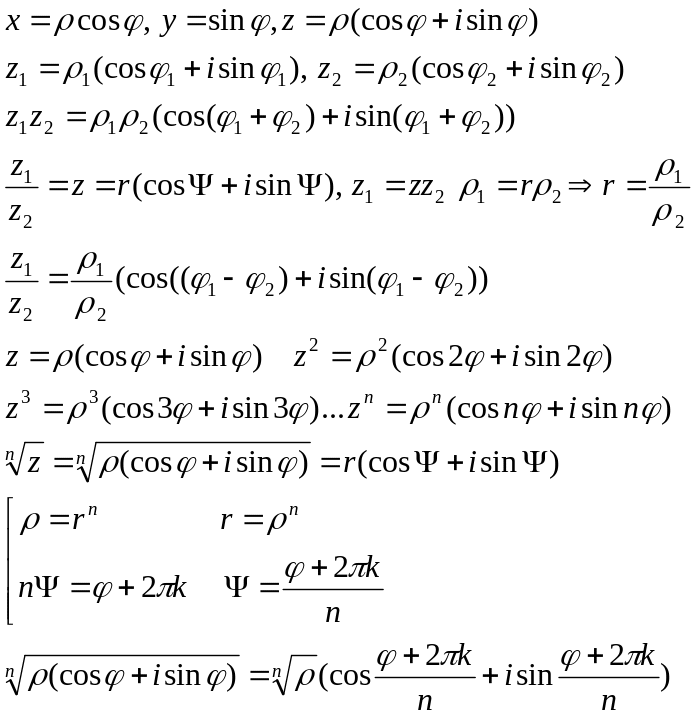Розклад многочлена на множники

P(x)=a0xⁿ+a1x^n-1 +a2x^n-2+….+a_n, z-корінь многочлена

P(x)=(x-z)P₁(x), Якщо P(x) без залишку ділиться на (x-z)^k і не ділиться на (x-z)^k+1, то число z наз коренем мног. P(x) кратності k. Многочлен n-го степеня завжди можна записати у вигляді

Розклад правильного раціонального дробу на суму елементарних дробів

Елементарні дроби:

A, M, N – дійсні числа

Нехай P(x)/Q(x) - раціональний дріб, тобто частка двох многочленів. Раціональний дріб P(x)/Q(x) наз. правильним, якщо степінь многочленна, який стоїть в чисельнику строго менше степеня, який стоїть в знаменнику. В противному випадку дріб наз. неправильним. Якщо раціональний дріб P(x)/Q(x) - неправильний, то розділивши чисельник на знаменник по правилу діл. многочленів, цей дріб можна записати у вигляді:

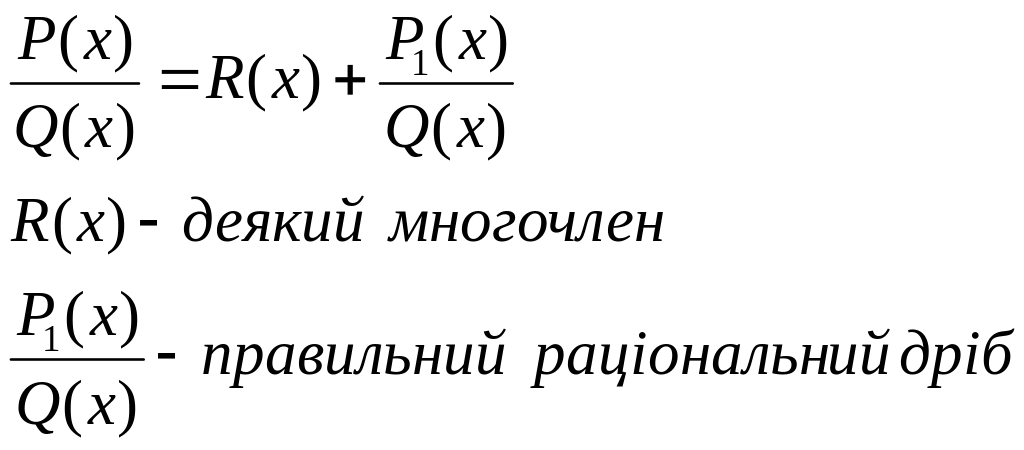
Оскільки інтегрувати многочлен можна, то залишається тільки навчитися інтегрувати правильний раціональний дріб.

Теорема

Якщо P(x)/Q(x) - правильний раціональний дріб, і , то цей дріб можна записати у вигляді 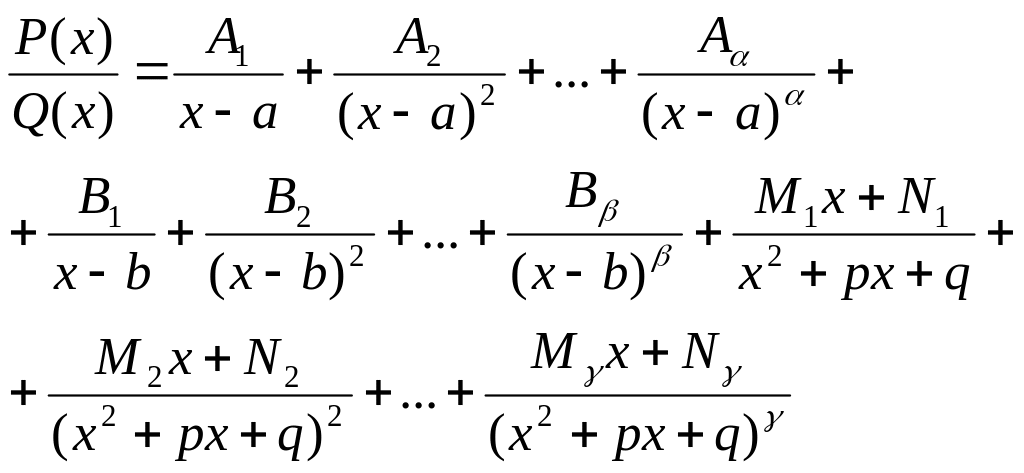де

Щоб знайти ці коефіцієнти застосовують метод невизначених коефіцієнтів.

Зауважимо, що скільки різних дійсних коренів має знаменник, стільки невизначених коефіцієнтів знаходяться підстановкою в тотожність дійсних коренів знаменника.

Інтегрування елементарних дробів.

Елементарні дроби двох видів:

Розглянемо випадок, коли ά=1

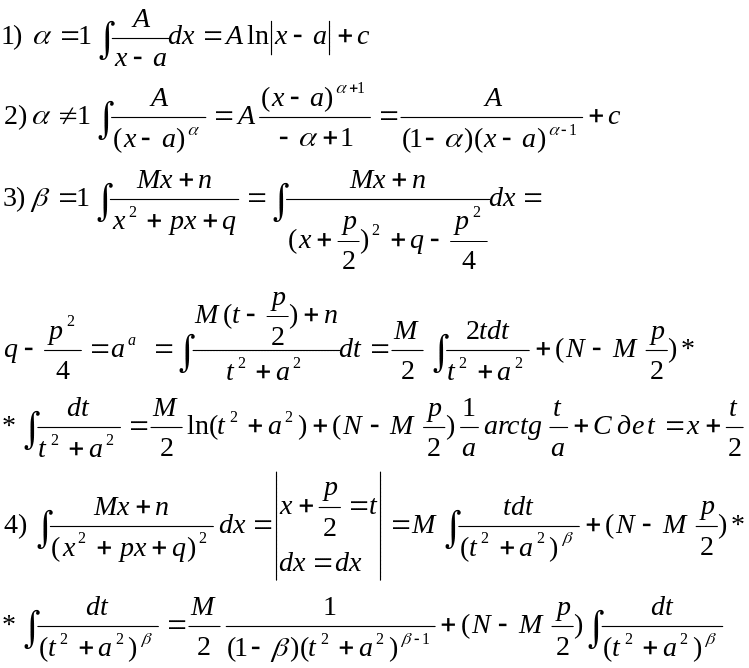Останні інтеграли обчислюються за допомогою рекурентної формули.

Інтегрування дробово-лінійних ірраціональностей

Покажемо, що даний інтеграл приводиться до інтегралу від раціонального дробу за допомогою підстановки.

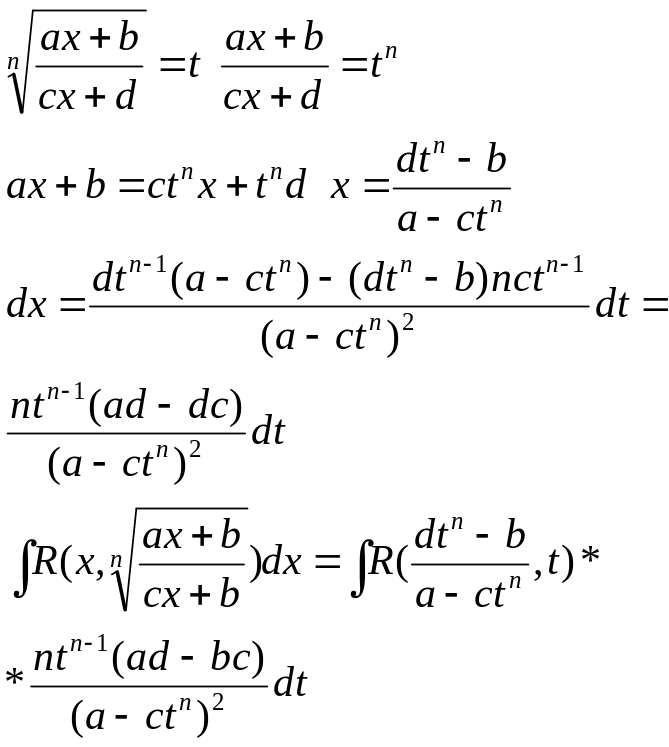
Зауважимо, що інтеграл від

обчислюється за допомогою метода підстановки

n=НКС знаменників (α,β,γ)

Інтегрування біноміальних диференціалів

Вираз виду: x^m(a+bxⁿ)^pdx, де m,n,p – раціональні числа. Чебишев довів, що інтеграл від біноміальних диференціалів обчислюється тільки в 3 випадках:

1) p – ціле.

Якщо p 0, то одержимо інтеграл від суми степеневих ф-цій, якщо p<0, то s=НСК(знамен. m,,n)

Тоді . - перша підстановка Чебишева..

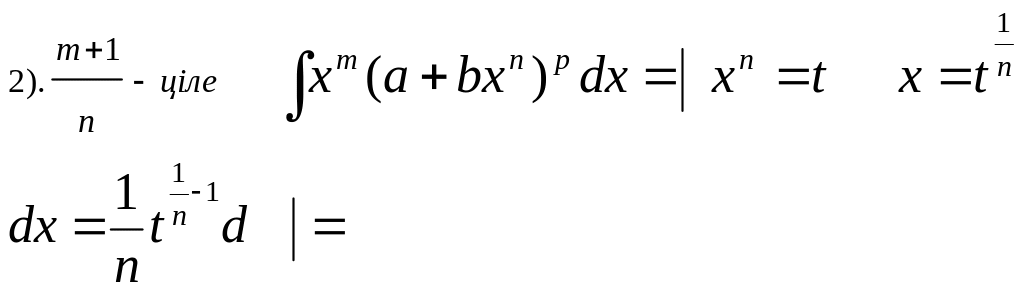
Оскільки (m+1)/n - за умовою ціле, то цілим буде і число (m+1)/n-1, а тому останній інтеграл перетворюється в інтеграл . Останній інтеграл обчислюється за допомогою підстановки - 2 підстановки Чебишева.

3)

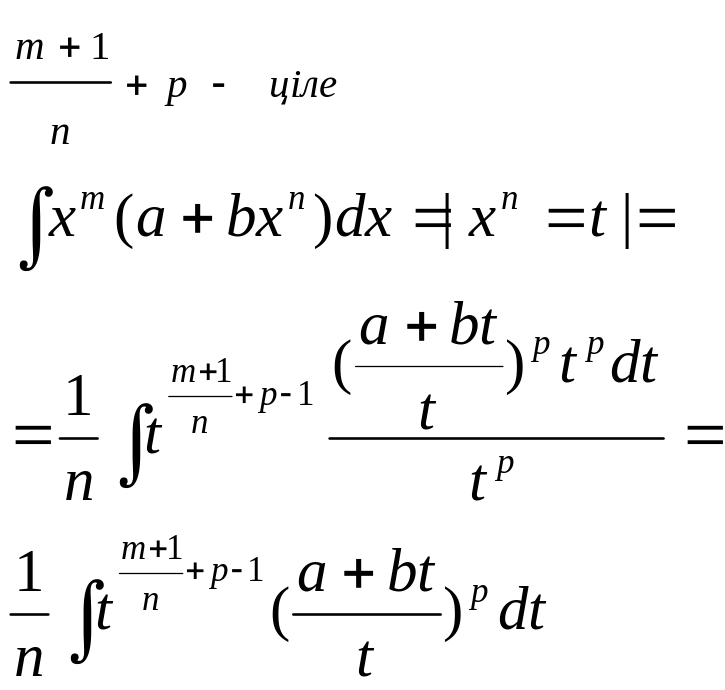
Оскільки (m+1)/n+p - ціле, то останній інтеграл є інтегралом від раціональної ф-ціі, яка залежить від , - 3 підстановка Чебишева.

Підстановки Ейлера

, де R – раціональна функ. до своїх аргументів, цей інтеграл приводиться до інтегралу від раціонального дробу в 3 випадках:

1. а>0 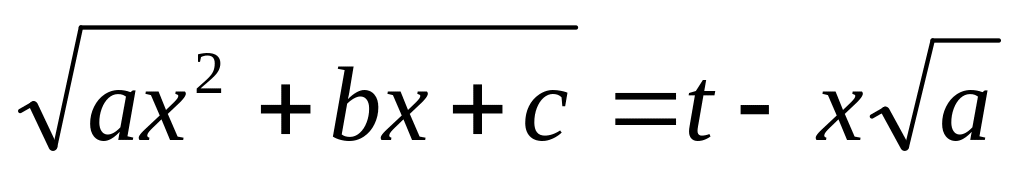1-підс Ейлера

2. с>0 -2 підс Ейлера

3. с>0

Д-мо(3 підстановку )

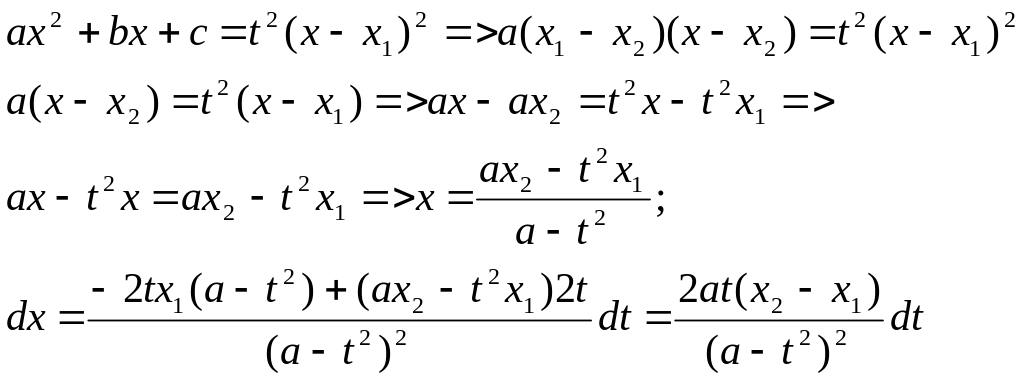
Підставляючи в початковий інтеграл замість х, dx та їх значення одержуємо

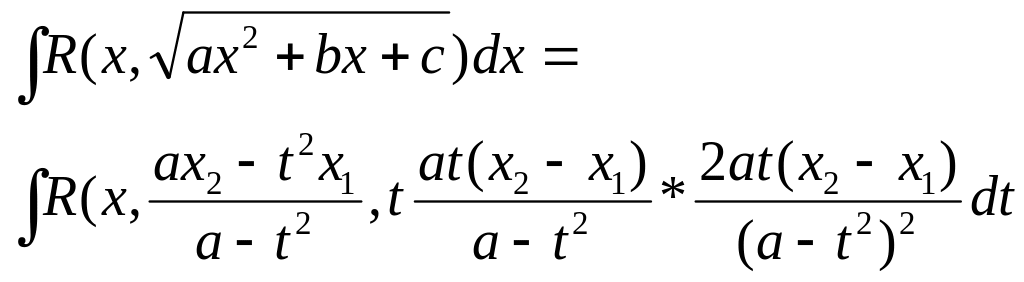
Підінтегральна функція я дробово-раціональною ф-єю, тому є функцією інтегровную

Інтегрування тригонометричних ф-цій

1) R-раціональна функція своїх аргументів. А останній інтеграл приводиться до інтегралу від раціонального дробу за допомогою підстановки універсальна триг.підстан.

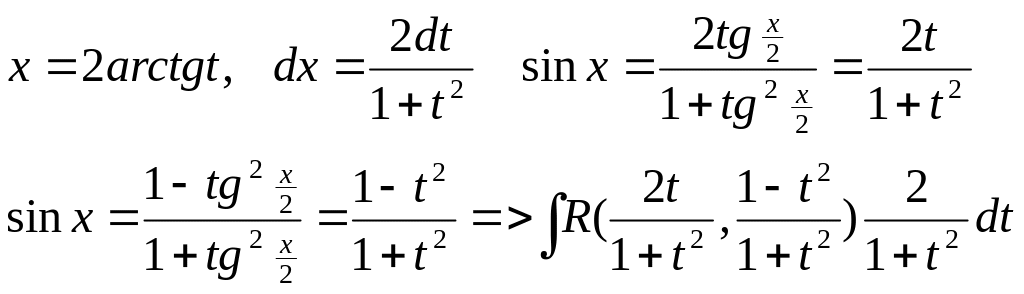
2)R(-sinx, cosx)=- R(sinx, cosx) то замін cosx=t;

3)R(sinx, -cosx)=-R(sinx, cosx) то замін sinx=t;

4)R(-sinx, -cosx)=R(sinx, cosx) то замін tgx=t;

Задача про обчислення площі криволінійної трапеції

К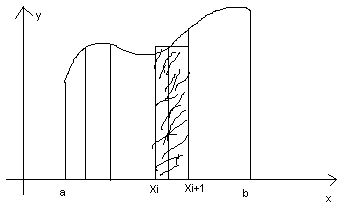 риволінійна трапеція – область, обмежена з боків x=a, x=b, знизу ох, зверху – f(x).

Розіб’ємо аb довільним способом на n частин. Через точки поділу проведемо прямі, паралельні оу. Ці прямі розбивають область на n криволінійних трапецій.

Візьмемо довільно ξi є [xi,xi+1] i=0..n-1 та замінимо кожну криволінійну трапецію прямокутником, основа якого є відрізок [xi,xi+1], а висота – значення f(ξi).

Прямокутник:

Трапеція:

Поняття визначеного інтегралу

Припустимо, f(x) є [a,b].

Формально зробимо слідуюче:

1). Довільним способом відрізок [a,b] розіб’ємо на n частин

2). Довільним способом вибираємо ξi є[xi,xi+1], і=0..n-1

3). Будуємо σ(f)=Σ_(i=1..n) f(ξi)Δx_i, Δx_i=x_i+1 +x_i , σ(f) – інтегральна сума Рімана для визначеного інтегралу. Значення цієї суми залежить від способу розбиття відрізку [a,b] на часткові відрізки та вибору точок ξ_і на кожному із часткових відрізків.

4). Λ=maxΔxi

Визначений інтеграл – скінченна границя lim _x0 σ(f) при умові, що ця границя не залежить від способу розбиття відрізка [a,b] на часткові відрізки та від вибору точок на цих відрізках.

Площа криволінійної трапеції дорівнює цьому інтегралу.

Необхідна умова існування визначеного інтегралу

Т.: Якщо існує то ф-ція f(x) обмежена на відрізку [a,b].

Довед: Від супротивного:

Припустимо, що існує ф-ція необмежена. Довільним способом відрізок [a,b] розіб’ємо на n частин

Оскільки f(x) не обмежена, то ця ф-ція буде необмежена хоча б на одному із відрізків.

Припустимо, f(x) необмежена на [x_k ,x_k+1]: /f(ξ)/>k

Довільним способом розіб’ємо [a,b] на n частин і для цього розбиття побудуємо інтегр. суму Рімана

за рахунок k-го доданку цієї суми набуває як завгодно великого значення, а тому скінченої границі така функція мати не може, що суперечить умові існування відзначеного інтегралу. Теорема доведена.

Достатні умови існування визначеного інтегралу

Інтегрованими на [a,b] є:

1). F(x) є c[a,b]

2). Кусково-неперервні, тобто ті, що мають скінченнне число точок розриву першого роду

3). Монотонні обмежені ф-ції

Визначений інтеграл зі змінною нижньою (верхньою) межею інтегрування

Припустимо, що f(x) є інтегрованою. Якщо ф-ція f(x) є C[a,b]

Візьмемо довільно x є [a,b]. Проведемо пряму паралельно оу. Оскільки f(x) є C[a,b] то існуватиме і:

1). - змінна верхня межа

2). змінна нижня межа

Визначений інтеграл зі змінною верхньою межою має такі властивості:

1. якщо існує , F(x)= то визначений інтеграл зі змінною верхньою межею: F(x)= є С[a,b]

2. якщо f(x)= є С[a,b], то f(x)єD[a,b] для всіх х є [a,b] F’(x)=f(x) Ф’(x)= - f(x)

Основна теорема інтегрального числення (формула Ньютона-Лєйбніца)

Т. : Якщо f(x) є C[a,b], a Ф’(х)=f(x) x є [a,b], то =Ф(b) - Ф(a)=Ф(x)/_a^b

Доведення

Оскільки f(x) є C[a,b], то F(x) = є D[a,b] для всіх x є [a,b] F’(x)=f(x), тобто F – первісна для f.

F(x)-Ф(х)=с=сonst, x є [a,b] F(a)-Ф(b)=c (F(a)=0) c= - Ф(a)

Якщо x=b, то F(b)-Ф(b)= -Ф(a); F(b)=Ф(b)-Ф(а)=

Властивості визначених інтегралів

Основні методи обчислення визначених інтегралів

І. Метод підстановки (метод заміни змінної)

II.Метод інтегрування частинами

Т.: Якщо дві ф. U=U(x) і V=V(x), мають неперервні похідні на відрізку [a, b] , тоді Мая місце слідуючи формула - формула інтегрування частинами у визначеному інтегралі.

Доведення:

Розглянемо диференціал від добутку: d(UV)=dUV+UdV інтегруючи обидві частини рівності

Розглянемо інтеграл:

Інтеграли Ейлера.

Ейлоровим інтегралом 1-го роду Г-ф-ції наз.

Зауважимо, що цей інтеграл має дві особливості:

1. Оскільки верхня межа інтегрування дор. Нескінченності, то це є невласний інтеграл 1-го роду.

2. А оскільки для α<1, то т.0 – є особливою точкою, то цей інтеграл є також інтегралом 2-го роду (тільки, якщо α<1).

Зауважимо, що визначена ф-ція Г(α) тільки для α>0.

Основні властивості Г-ф-ції:

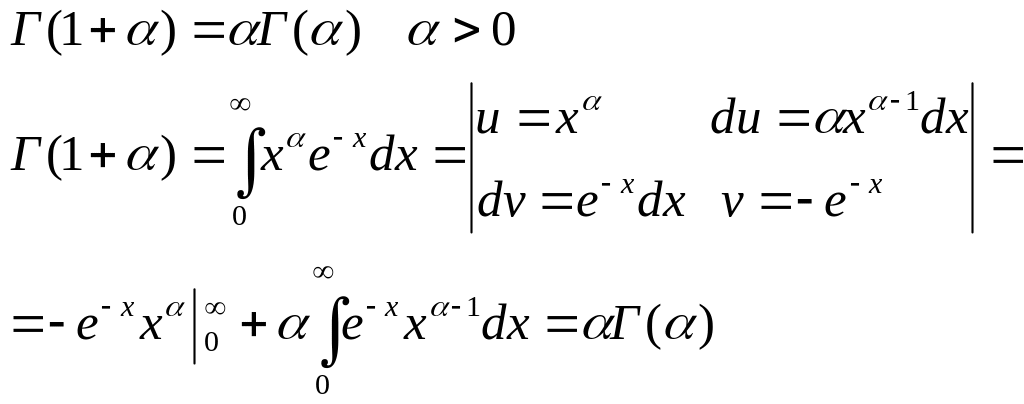
У частковому випадку, якщо α=n

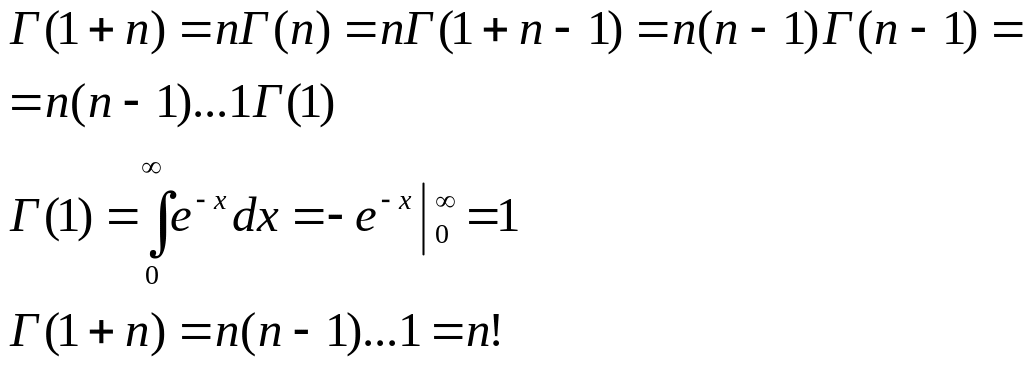
Г-ф-ція – є узагальнення для факторіала з нецілим значенням n.

2). Формула доповнення

Ейлеровим інтегралом II роду, або β функцією називають

Зауважимо, цей інтеграл має 2 особливі точки :

• Якщо α<1, x=0

• Якщо β<1, x=1

Якщо і α>1 i β>1 то цей інтеграл є звичайним визначеним

Властивості:

1. Властивість симетрії

Доведення:

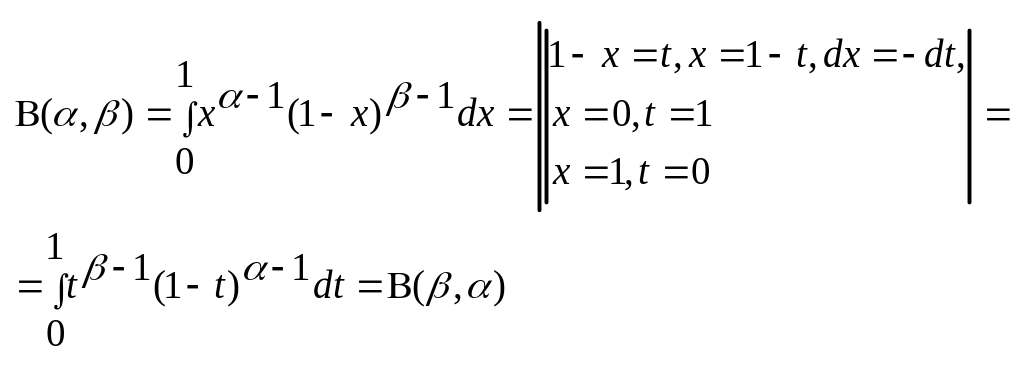2. Інше представлення β функції

Покажемо, що

Доведення

Зв'язок між α та β функт.

Для всих α>0, β>0

Β(α,β)=(Г(α)Г(β))/(Г(α+β))

Невласні інтеграли першого роду (інтеграли з нескінченними межами інтегрування).

Припустимо, що f(x) визначена і на довільному відрізку [a, A] A>a; границя інтегралу (1), незалежно від того, існує ця границя, чи ні, наз. невласним інтегралом з нескінченною верхньою межею інтегрування і позначається так:

(2)

Якщо границя (1) існує, і нескінченна, то невласний інтеграл (2) наз. збіжним. В противному випадку – розбіжним.

Припустимо, що ф. f(x), визначена для a, і на довільному відрізку [B,b] B<b ф. f(x) – інтегрована, тобто

Границя цього інтегралу незалежно від того, існує ця границя, чи ні, називаються невласним інтегралом з нескінченною нижньою границею і символічно позначають так:

Якщо границя інтеграла , існує і скінченна, то інтеграл наз. збіжним в протилежному випадку – розбіжним.

Аналогічно вводиться означення невласного інтегралу у якого обидві межі інтегрування дорівнюють нескінченності, а саме:

Ознаки порівняння невласних інтегралів і роду

1) якщо ф. , ці функції інтегровані на інтервалі

(1) (2) тоді із

із збіжності інтегралу (1) випливає збіжність інтегралу (2)

із збіжності інтегралу (2) випливає збіжність інтегралу (1)

із розбіжності (2) випливає розбіжність (1)

y

y=f(x)

y=g(x)

x

a

Оск. графіки функцій функцій

2) якщо є два невласних інтеграли І роду, у яких підінтегральні функції невід`ємні.

Тоді якщо існує і дор. числу с, тоді:

якщо із збіжн. (2) збіжн. (1)

якщо із збіжн. (2) збіжн. (1)

якщо , то невласні інтеграли (1) і (2) ведуть себе однаково, або одночасно вони є інтегралами збіжними або одночасно розбіжні.

Невласні інтеграли іі роду

(невласні інтеграли від необмежених функцій)

Припустимо, що ф. f(x) визначена на пів проміжку x[a;b); і в околі т. b ф.f(x) – необмежена

а ле на довільномі відрізку [a,b-] 0<<b-a

(x) – інтегрована на дов. відрізку [a,b-]

Границя цього інтегралу: (1) незалежно від того, існує вона, чи ні, наз. невласним інтегралом ІІ роду, або невласним інтегралом від необмеженої функції:

(2), і так за означенням

Якщо границя (1) існує і нескінченна, то інтеграл (2) наз. збіжним і в противному випадку інтеграл (2) наз. розбіжним.

Аналогічно вводиться означення невласного інтеграла, у якого або нижня меж інтегрування або внутрішня ...

т. в околі яких ф. необмежена, наз. особливими точками.

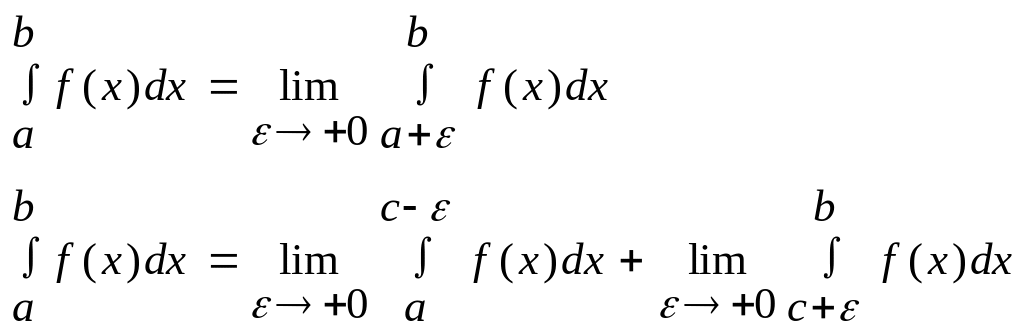
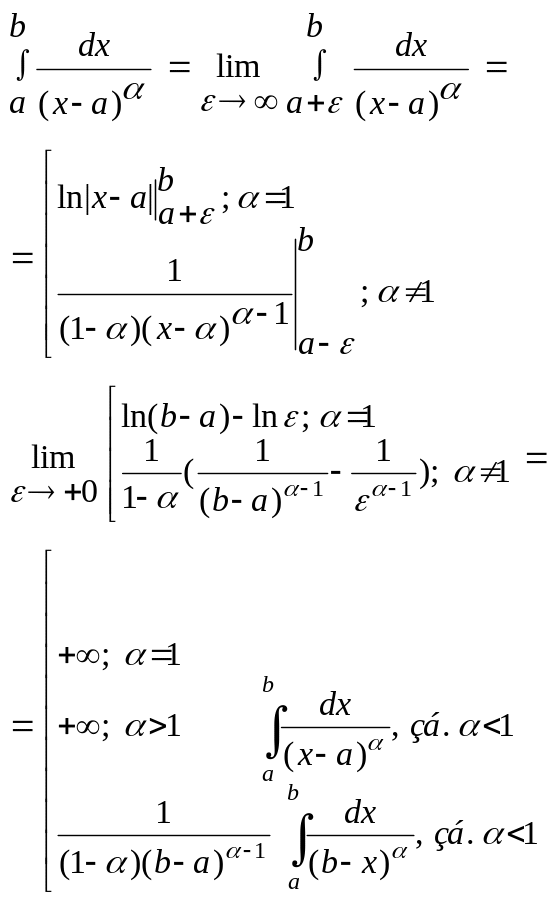
Ознака порівняння невласних інтегралів ІІ роду

1) якщо ф. (x) і g(x) – не .... 0≤x≤g(x) ….. (a, b]

від`ємні і інтегровані на напівінтервалі [a, b], тоді із збіжності інтеграла

із розбіжності інтеграла

2) якщо ф. f(x) і g(x) – невід`ємні

f(x)0, (X)0, x[a, b) тоді

якщо

а) 0≤с< зб. зб.

б) 0<с≤ зб. зб.

в) , то і , то такі інтеграли одночасно є збіжними інтегралами або одночасно є розбіжними інтегралами.

І. Обчислення площі плоскої фігури

1) Обчислення площі обмеженої лініями, рівняння яких задані явно.

Із гометр. інтерпретації визн. інтегралу маємо фігуру яка обмежене зверху y=f(x), з боків лініями а, b, знизу відрізком ox, то

Якщо плоска фігура обмежена з боків х=а х=b a знизу кривими то:

з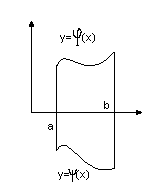 ауважимо якщо область має інший вигляд за допомогою прямих паралельних координатним осям цю обл. розбивають на частини кожна з яких має приведений вище вигляд після цього S обчислюються кожної з площин і додається.

2) Обчислення площі криволінійної трапеції, яка обмежена кривою, заданою параметричним рівняннями

знизу ab, зверху

Відомо із гометричної інтерпретації визн. інтегралу.

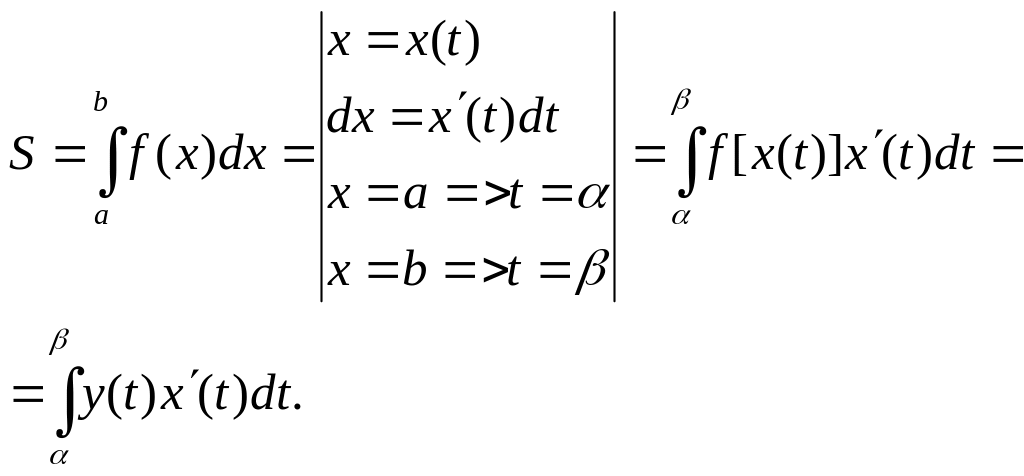
3)Обчислення площі криволінійного сектора

Криволінійним сектором наз. Фігура яка обмежена променями φ = α φ = β ρ=ρ(φ),

Щ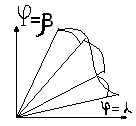 об обчислити S криволінійного сектора ми довільним способом відрізок αβ розіб’ємо на n частин.

замінимо кожний із одержаних криволінійних секторів – круговим сектором.

ІІ. Обчислення довжини дуги кривої

1) Випадок явного задання кривої:

A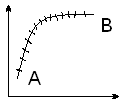 B:y=f(x) xє[a,b] f’(x)єC[a,b]

Щоб обчислити довжину дуги цієї кривої довільним способом цю криву розіб’ємо на n частин точками.

A = A₀,A₁,A₂ … A_i,A_i+1,A_n=B; A_i(x_i f(x_i)), A_i+1(x_i+1 f(x_i+1))

З’єднаємо всі точки відрізками прямих одержимо ломану вписану в криву АВ, довжина якої:

2) Випадок параметричного задання.

відомо, що l дуги кривої обчислюється за фор-лою.

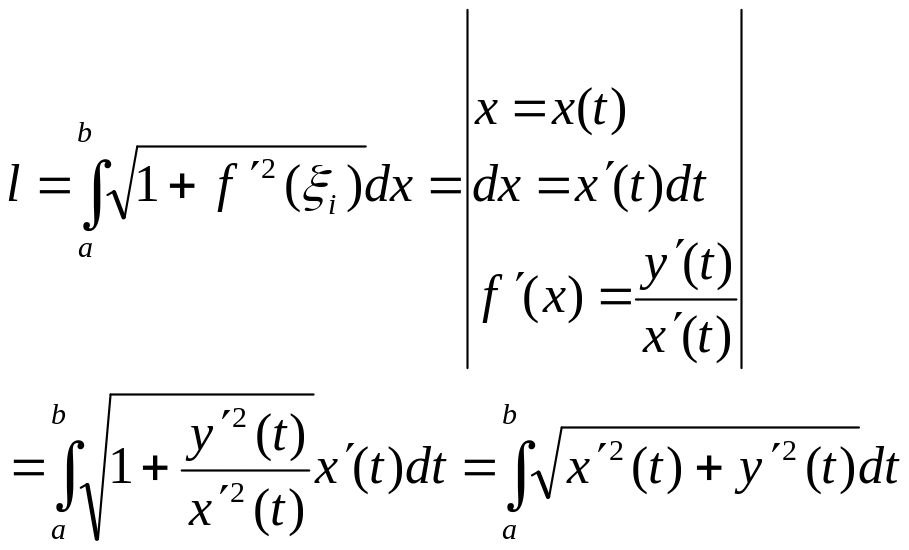
3).Задана рівнянням в полярних координатах

АВ: ρ= ρ(φ)φє[α,β]; ρ’(φ)є[α,β]

Використовуючи фор-ли зв’язку полярних координат між декартовими маємо

одержані є параметричним заданням кривої, а тому

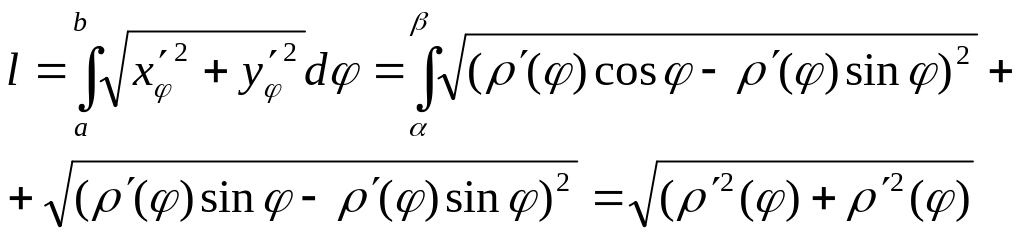
ІІІ Обчислення об’ємів тіл довільної форми

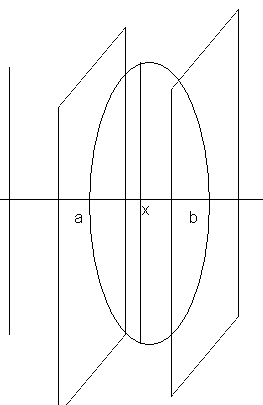
Тіло між площинами х=а х= b

Щоб знайти об’єм данного тіла з цією метою відрізок аb довільним способом розіб’ємо на n-частин

Через кожну точку із цих точок проведемо площини перпендикулярну до вісі ОХ, ці площини розіб’ють тіло на n частин

Дов і замінимо тіло x=x_i x=x_i+1 - циліндром основою якого фігура яка одержана в перерізі

S(ξ)– плоша основи

V_i= S(ξ)Δx_i

2).Об‘єм тіла обертання:

Припустимо, що задана криволінійна трапеція

f(x)≥0, f(x)єC[a,b] будемо обертати це тіло навколо вісі ОХ утвор. тіло наз. тілом обертання.

Візьмемо довільно хє[a,b], через дану т. проведем переріз, перпендикулярний до вісі ОХ

Використовуючи ф-лу об’єма тіла дов. форми:

- ф-ла для об’єма тіла обертання.

IV Обчислення площі поверхні тіла обертання

Припустимо, що на площені ХОУ задана криволінійна трапеція, яка обмеж. знизу [a,b] на вісі ОХ, з боків – прямими х=а, х=в, зверху – кривою у=f(x).

Будемо обертати цю трапецію навколо вісі ОХ. Одержемо тіло обертання.

Площа поверхні цього тіла обчислюється за ф-лою:

Якщо крива, яка обмеж. криволінійну трапецію зверху задана параметричним р-ням: