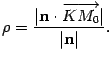2.3. Эквивалентные системы векторов

Две системы n-мерных векторов:

a1,a2,…,ak (2.2)

и

b1,b2,…,bl(2.3)

называются эквивалентными, если любой вектор системы (2.2) ли-

нейно выражается через (2.3) и наоборот.

Можно доказать, что ранги эквивалентных систем равны. Преоб-

разования системы векторов, не изменяющие ее ранг, называются эк-

вивалентными. Такими преобразованиями являются:

1) изменение нумерации векторов;

2) удаление нулевого вектора;

3) удаление линейной комбинации векторов;

4) умножение любого вектора системы на число, отличное от нуля;

5) прибавление к одному из векторов системы линейной комби-

нации остальных векторов системы.

24

Ортогональной системой векторов n-мерного евклидова про-

странства называется такая система из n векторов, в которой каждый

из векторов ортогонален другому; т.е. система a1, a2,.., anназыва-

ется ортогональной, если ( ai,aj ) = 0 при i ≠ j .

Доказано, что любая ортогональная система векторов евклидова

пространства является его базисом. Если, помимо ортогональности,

каждый из векторов системы является единичным, т.е. ( ei,ej ) =1 то

такой базис называется ортонормированным. Такой базис является

наиболее удобным для решения задач аналитической геометрии.

4) Скалярным произведением n-мерных векторов а(век) = (a1,a2,…,an )и

b(век) = ( b1,b2 , ...,bn ) называется число, обозначаемое (a(век),b(век)) и равное сум-

ме произведений соответствующих координат:

(a(век),b(век))=a1b2+a1b2+…+anbn=∑aibi

Если, например, предприятие реализует 4 вида товаров в количе-

ствах 10, 20, 15 и 5 единиц соответственно по ценам 2, 3, 4 и 6 денеж-

ных единиц, то скалярное произведение вектора цен с = (2, 3, 4, 6) на

вектор объемов продаж х = (10, 20, 15, 5) даст ожидаемую выручку,

которая составит (с(век), х(век)) = 2 ּ10 + 3 ּ20 + 4 ּ15 + 6 ּ5 = 20 + 60 + 60 + 30

= 170 (денежных единиц).

Модулем (длиной) n-мерного вектора а(век) = ( а1 ,а2 , ..., аn ) называется

число |a(век)|=√(a(век),a(век))=√(a1^2+a2^2+…+an^2

Углом φ между n-мерными векторами а(век) и b(век) называется угол,

косинус которого вычисляется по формуле:

cosф=(a(век),b(век))/|a(век) |*|b(век)|=

расстояние d(А, В) между точками А(х1 , х2 ,… , хn) и

В( у1, у2… уn) n-мерного пространства называется длина вектора

АВ(век), т.е. d(A,B)= √(AB(век),AB(век))= √(y1-x1)^2+(y2-x2)^2+…+(yn-xn)^2

Справедливы следующие свойства скалярного произведения:

1. (a,b) = (b,a) (коммутативность);

2. (λa,b) = (a,λb) = λ (a,b) (вынесение числового множителя);

3. (a + b,c) = (a,b) + (b,c) (дистрибутивность);

4. (a,a) ≥ 0 , причем знак равенства выполняется лишь при усло-

вии a = 0 (неотрицательность скалярного квадрата вектра).

Линейное n-мерное векторное пространство, в котором введена

операция скалярного умножения векторов, удовлетворяющая свой-

ствам 1– 4, называется евклидовым пространством.

5) Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Произведение не является ни коммутативным, ни ассоциативным (оно является антикоммутативным) и отличается от скалярного произведения векторов. Во многих задачах инженерии и физики нужно иметь возможность строить вектор, перпендикулярный двум имеющимся — векторное произведение предоставляет эту возможность. Векторное произведение полезно для «измерения» перпендикулярности векторов — длина векторного произведения двух векторов равна произведению их длин, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны.

Векторное произведение определено только в трёхмерном и семимерном пространстве. Результат векторного произведения, как и скалярного, зависит от метрики Евклидова пространства.

В отличие от формулы для вычисления по координатам векторов скалярного произведения в трёхмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат или, иначе, её «хиральности».

Векторным произведением вектора на вектор в пространстве называется вектор , удовлетворяющий следующим требованиям:

• длина вектора равна произведению длин векторов и на синус угла 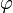; между ними

• вектор ортогонален каждому из векторов и

• вектор направлен так, что тройка векторов является правой.

• в случае пространства 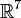требуется ассоциативность тройки векторов .

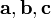Обозначение:

В литературе^[1] определение векторного произведения может даваться по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах в правой и левой прямоугольной системе координат. А далее выводится данное выше определение, а также определение правой и левой тройки векторов.

Также для исходного определения может быть взят набор алгебраических свойств векторного произведения, а из них выводиться остальное.

11) Предложение 11.1 Пусть плоскость задана уравнением и дана точка . Тогда расстояние от точки до плоскости определяется по формуле

(11.7)

Доказательство. Расстояние от точки до плоскости -- это, по определению, длина перпендикуляра , опущенного из точки на плоскость (рис. 11.9).

Рис.11.9.Расстояние от точки до плоскостиВектор и нормальный вектор n плоскости параллельны, то есть угол между ними равен 0 или , если вектор n имеет направление противоположное, указанному на рис. 11.9. Поэтому

Откуда

(11.8)

Координаты точки , которые нам неизвестны, обозначим . Тогда . Так как , то . Раскрыв скобки и перегруппировав слагаемые, получим

(11.9)

Точка лежит на плоскости , поэтому ее координаты удовлетворяют уравнению плоскости: . Отсюда находим, что . Подставив полученный результат в формулу (11.9), получим . Так как , то из формулы (11.8) следует формула (11.7).

12) Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

в котором по крайней мере один из коэффициентов отличен от нуля.

Классификация