1. Односторонний предел в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева) и правосторонним пределом (или пределом справа).

Определения. Пусть задана числовая функция — предельная точка области

Число называется правосторонним пределом функции при стремящемся к если

Число называется левосторонним пределом функции при стремящемся к если

Обозначения Правосторонний предел принято обозначать любым из нижеследующих способов:

Аналогичным образом для левосторонних пределов приняты обозначения:

Для того, чтобы существовал предел (A – число)

по проколотой окрестности точки x₀ необходимо, чтобы в точке x₀ существовали пределы слева и справа и они были равны между собой.

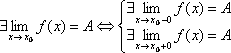
Пусть функция определена на множестве , имеющем элементы вне любой окрестности нуля. В этом случае точка называется пределом функции на бесконечности, если для любой её малой окрестности найдётся достаточно большая окрестность нуля, что значения функции в точках, лежащих вне этой окрестности нуля, попадают в эту окрестность точки .

2. Т.1: Предел постоянной равен самой постоянной Доказательство следует из определения предела функции, так как если с = const.

Т.2: (о связи функции с ее пределом). Для того чтобы необходимо и достаточно выполнение равенства где — б.м. при х а

— б.м., х a

Запишем цепочку равносильных утверждений, следующих из определения предела функции и определения б.м.:

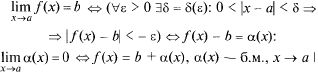
Т.3: Предел суммы конечного числа функций, имеющих пределы при х а, равен сумме их пределов

Пусть тогда по теореме 2 имеем где — б.м. при х а, следовательно, Используя теорему 1 о б.м., заключаем, что — б.м. при и по теореме 2 получаем равенство b1 + b2

Т.4: Предел произведения конечного числа функций, имеющих пределы при х а, равен произведению пределов. Методика доказательства аналогична доказательству Т.3. Следствие. Постоянный множитель можно выносить за знак предела.

Т.5: Предел отношения двух функций, имеющих пределы при х а, равен отношению их пределов (если предел знаменателя не нуль), т.е.

Пусть тогда, используя Т.2, аналогично доказательству Т.3 запишем

где Числитель последней дроби по леммам о б. м. является б.м. Покажем, что является функцией ограниченной, тогда дробь по теореме 2 о б.м. является б.м., и по Т.2:

Имеем в некоторой окрестности т. а для любого > 0 вследствие справедливости

т.е. ограниченность доказана.

3. Непрерывная функция — функция без «скачков», то есть такая у которой малые изменения аргумента приводят к малым изменениям значения отображения.

Непрерывная функция, вообще говоря, — синоним понятия непрерывное отображение, тем не менее, чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающих вещественные значения.

Пусть и .

Функция f непрерывна в точке , если для любого ε > 0 существует δ > 0 такое, что

Функция f непрерывна на множестве E, если она непрерывна в каждой точке данного множества.

В этом случае говорят, что функция f класса C⁰ и пишут: или, подробнее, .

Свойства

►Непрерывная функция является локально ограниченной.

►Непрерывная функция сохраняет свой знак в некоторой окрестности точки непрерывности.

►Сумма и произведение двух непрерывных в данной (одной и той же) точке также является функцией, непрерывной в данной точке.

►Частное от деления двух функций непрерывных в данной точке также является функцией, определённой в некоторой окрестности данной точки и непрерывной в ней.

►Если функция f непрерывна в точке a, и функция g непрерывна в точке b = f(a), то их композиция является функцией, непрерывной в точке a.

►Если функция, непрерывная на отрезке, принимает на его концах значения разных знаков, то на отрезке есть точка, в которой функция обращается в нуль.

►Если функция, непрерывная на отрезке, принимает в двух заданных точках какие-либо значения, то для всякого значения, находящегося между ними, найдётся точка, лежащая на отрезке между двумя заданными точками, где функция принимает данное значение.

►Иначе говоря, областью значений непрерывной на отрезке функции является отрезок.

►Функция, непрерывная на отрезке, ограничена на нём.

►Более того на отрезке есть точка, где функция принимает максимальное (минимальное) значение.

►Непрерывная функция на отрезке равномерно непрерывна на нём.

►Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда функция строго монотонна на данном отрезке.

►Функция, монотонная на отрезке, непрерывна на нём тогда и только тогда, когда образ отрезка сам является отрезком, причём концы отрезка области определения переходят в концы области значений.

4.Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.

Бесконечно малая величина

Последовательность a_n называется бесконечно малой, если . Например, последовательность чисел — бесконечно малая.

Функция называется бесконечно малой в окрестности точки x₀, если .

Функция называется бесконечно малой на бесконечности, если либо .

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если , то f(x) − a = α(x), .

Свойства бесконечно малых

►Сумма конечного числа бесконечно малых — бесконечно малая.

►Произведение бесконечно малых — бесконечно малая.

►Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.

►Если a_n — бесконечно малая последовательность, сохраняющая знак, то — бесконечно большая последовательность.

Сравнение бесконечно малых

Отношение бесконечно малых величин образует так называемую неопределённость .

5. Эквивалентные величины

Если , то бесконечно малые величины α и β называются эквивалентными ( ).

Очевидно, что эквивалентные величины являются частным случаем бесконечно малых величин одного порядка малости.

При справедливы следующие соотношения эквивалентности (как следствия из т. н. замечательных пределов):

►

►

►

►

Теорема

Предел частного (отношения) двух бесконечно малых величин не изменится, если одну из них (или обе) заменить эквивалентной величиной.

Данная теорема имеет прикладное значение при нахождении пределов

Пример использования

Найти

Заменяя sin2x эквивалентной величиной 2x, получаем

6. БЕСКОНЕЧНО БОЛЬШАЯ ФУНКЦИЯ

функция переменного , к-рая в данном процессе изменения становится и остается по абсолютной величине больше любого наперед заданного числа. Точнее, функция , определенная в окрестности точки , наз. бесконечно большой функцией при , стремящемся к , если для любого числа найдется такое число d = d (M)>0, что для всех и таких, что выполняется неравенство .Этот факт записывается так:

Аналогичным образом определяются

Напр.,

означает, что для любого найдется такое , что для всех выполняется неравенство . Изучение Б. б. ф. может быть сведено к изучению бесконечно малых функций, т. к. если есть Б. б. ф., то функция является бесконечно Малой.

Соотношение между бесконечно малыми и бесконечно большими функциями

Теорема 1. Если функция f(x) является бесконечно большой при x→a, то функция 1/f(x) является бесконечно малой при x→a.

Доказательство. Возьмем произвольное число ε>0 и покажем, что при некотором δ>0 (зависящим от ε) при всех x, для которых |x – a|<δ, выполняется неравенство , а это и будет означать, что 1/f(x) – бесконечно малая функция. Действительно, так как f(x) – бесконечно большая функция при x→a, то найдется δ>0 такое, что как только |x – a|<δ, так |f(x)|>1/ ε. Но тогда для тех же x .

Примеры.

Ясно, что при x→+∞ функция y=x2+1 является бесконечно большой. Но тогда согласно сформулированной выше теореме функция – бесконечно малая при x→+∞, т.е. .

Теорема 2. Если функция f(x) - бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y=1/f(x) является бесконечно большой функцией.

Примеры.

1.

2.

3. , так как функции и - бесконечно малые при x→+∞, то , как сумма бесконечно малых функций есть функция бесконечно малая. Функция же является суммой постоянного числа и бесконечно малой функции. Следовательно, по теореме 1 для бесконечно малых функций получаем нужное равенство.

Таким образом, простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A≠ 0

7. 4.2. Понятие о точках разрыва и их классификация.

Различают три типа точек разрыва.

Разрыв 1-го рода (конечный разрыв).

Односторонние пределы конечные, но не равные , называется скачком функции в точке х₀.

Разрыв 2-го рода (бесконечный разрыв).

Если хотя бы один из односторонних пределов равен бесконечности или не существует, то х₀-точка разрыва 2-го рода.

Все вышесказанное относится к точке х₀, не являющейся границей области определения функции.

Если х₀ граница области определения, то в этой точке рассматривается односторонняя непрерывность.

8. Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием.

Определение

Пусть в некоторой окрестности точки определена функция Производной функции f в точке x₀ называется предел, если он существует,

Общепринятые обозначения производной функции y = f(x) в точке x₀:

Геометрический и физический смысл производной

Тангенс угла наклона касательной прямой

Если функция имеет конечную производную в точке x₀, то в окрестности U(x0) её можно приблизить линейной функцией

Функция fl называется касательной к f в точке x₀. Число f'(x₀) является угловым коэффициентом или тангенсом угла наклона касательной прямой.

Скорость изменения функции

Пусть s = s(t) — закон прямолинейного движения. Тогда v(t₀) = s'(t₀) выражает мгновенную скорость движения в момент времени t₀. Вторая производная a(t₀) = s''(t₀) выражает мгновенное ускорение в момент времени t₀.

Вообще производная функции y = f(x) в точке x₀ выражает скорость изменения функции в точке x₀, то есть скорость протекания процесса, описанного зависимостью y = f(x).

Дифференцируемость

Правила дифференцирования общих функций

(известно как «правило Лейбница»)

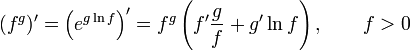
— Правило дифференцирования сложной функции

Дифференцируемая функция

Производная f'(x₀) функции f в точке x₀, будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция f является дифференцируемой в точке x₀ тогда и только тогда, когда её производная в этой точке существует и конечна:

Для дифференцируемой в x₀ функции f в окрестности U(x₀) справедливо представление

f(x) = f(x₀) + f'(x₀)(x − x₀) + o(x − x₀) при

Замечания

►Назовём Δx = x − x₀ приращением аргумента функции, а Δy = f(x₀ + Δx) − f(x₀) приращением значения функции в точке x₀. Тогда

►Пусть функция имеет конечную производную в каждой точке Тогда определена произво́дная фу́нкция

►Функция, имеющая конечную производную в точке, непрерывна в ней. Обратное не всегда верно.

►Если производная функция сама является непрерывной, то функцию f называют непреры́вно дифференци́руемой и пишут: