
9. Производная обратной функции
Дифференцируемая монотонная функция f:[a, b] → R с необращающейся в нуль производной имеет обратную дифференцируемую функцию f -1, производная которой вычисляется по формуле
![]()
![]()
Производная параметрически заданной функции
Если функция f задана параметрически
x = φ(t), y = ψ(t), α < t < β,
где y = f(x) и функции φ и ψ дифференцируемы, причем φ'(t) ≠ 0, то
![]()
![]()
Производная неявно заданной функции
Если y = f(x) - дифференцируемая функция, заданная уравнением F(x, y) = 0, т. е. F(x, f(x)) ≡ 0 на некотором интервале [a, b], то во многих случаях ее производную можно найти из уравнения
![]()
![]()
10. Дифференциа́л— линейная часть приращения функции или отображения. Это понятие тесно связано с понятием производной по направлению.
Определения для функций
Дифференциал гладкой вещественнозначной функции f, определённой на M (M — гладкое многообразие), представляет собой 1-форму, обычно обозначается df и определяется соотношением
![]()
где
![]() обозначает производную f по направлению
вектора X в касательном расслоении M.
обозначает производную f по направлению
вектора X в касательном расслоении M.
Геометрический смысл дифференциала
![]() мы выясним, исходя из найденного ранее
геометрического смысла производной.
Поскольку производная
мы выясним, исходя из найденного ранее
геометрического смысла производной.
Поскольку производная
![]() -- это угловой коэффициент
-- это угловой коэффициент![]() касательной к графику функции при
касательной к графику функции при
![]() ,
то дифференциал
,
то дифференциал
![]() --
это приращение ординаты
--
это приращение ординаты
![]() точки касательной
точки касательной
![]()
к графику функции
![]() ,
когда абсцисса точки касательной
получает приращение
,
когда абсцисса точки касательной
получает приращение
![]() :
:
![]()
Приближённые вычисления с помощью дифференциала
Формулу
![]()
задающую определение дифференциала, можно записать в виде приближённого равенства
![]()
если считать (при малых
![]() )
значение бесконечно малой величины
)
значение бесконечно малой величины
![]() много меньшим, чем
.
Перенося
много меньшим, чем
.
Перенося
![]() в правую часть, получаем:
в правую часть, получаем:
![]()
где
![]() .
С учётом выражения дифференциала через
частные производные, находим, что
.
С учётом выражения дифференциала через
частные производные, находим, что
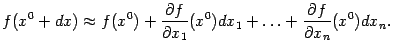
Эту формулу можно применять для
приближённого вычисления значений
функции
![]() в точках
,
если известны значения
и её частных производных
в точках
,
если известны значения
и её частных производных
![]() в точке
в точке
![]() .
.
11. Производные и дифференциалы высших порядков
Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производной функции f и обозначается f". Таким образом,
f"(x) = (f'(x))'.
Если дифференцируема (n - 1)-я производная функции f, то ее n-й производной называется производная от (n - 1)-й производной функции f и обозначается f(n). Итак,
f(n)(x) = (f(n-1)(x))', n ϵ N, f(0)(x) = f(x).
Число n называется порядком производной.
Дифференциалом n-го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом,
dnf(x) = d(dn-1f(x)), d0f(x) = f(x), n ϵ N.
Если x - независимая переменная, то
dx = const и d2x = d3x = ... = dnx = 0.
В этом случае справедлива формула
dnf(x) = f(n)(x)(dx)n.
12. Условия монотонности функции
(Критерий монотонности функции, имеющей
производную на интервале) Пусть функция
![]() непрерывна на (a,b),
и имеет в каждой точке
непрерывна на (a,b),
и имеет в каждой точке
![]() производную f'(x).
Тогда
производную f'(x).
Тогда
f возрастает на (a,b)
тогда и только тогда, когда
![]()
f убывает на (a,b)
тогда и только тогда, когда
![]()
(Достаточное условие строгой монотонности
функции, имеющей производную на интервале)
Пусть функция
непрерывна на (a,b),
и имеет в каждой точке
производную f'(x).
Тогда если
![]() то f строго возрастает на
(a,b);
то f строго возрастает на
(a,b);
если
![]() то f строго убывает на
(a,b).
то f строго убывает на
(a,b).
Обратное, вообще говоря, неверно. Производная строго монотонной функции может обращаться в ноль. Однако, множество точек, где производная не равна нулю, должно быть плотно на интервале (a,b). Точнее имеет место
(Критерий строгой монотонности функции,
имеющей производную на интервале) Пусть
![]() и всюду на интервале определена
производная f'(x).
Тогда f строго возрастает
на интервале (a,b)
тогда и только тогда, когда выполнены
следующие два условия:
и всюду на интервале определена
производная f'(x).
Тогда f строго возрастает
на интервале (a,b)
тогда и только тогда, когда выполнены
следующие два условия:
![]()
Аналогично, f строго убывает на интервале (a,b) тогда и только тогда, когда выполнены следующие два условия:
![]()
![]()
