
Билет 32:
Сформулируем некоторые свойства определенного интеграла в предположении, что подынтегральная функция ограничена на отрезке, по которому она интегрируется.
Если
функция интегрируема на [ a ; b ], то
она интегрируема на любом отрезке
![]()
Для
любых a , b и c
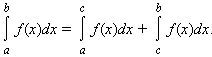
Интеграл
обладает свойством линейности: для
любых функций f ( x ) и g ( x ) и любой
постоянной A
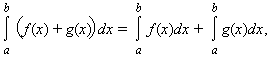
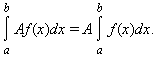
Если f ( x ) и g ( x ) интегрируемы на [ a ; b ], то f ( x ) · g ( x ) также интегрируема на этом отрезке.
Если
f ( x ) – периодическая функция с
периодом T , то для любого a
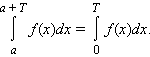
Для определенных интегралов верны также следующие оценки (предполагается, что функции f и g интегрируемы на [ a ; b ]).
Если
f ( x ) ≥ g ( x ), то
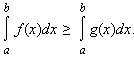 В
частности, если f ( x ) ≥ 0, то
В
частности, если f ( x ) ≥ 0, то
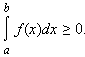
Если
f ( x ) ≥ 0 для любого
![]() и
существует
и
существует
![]() такое,
что
такое,
что
![]() причем
f ( x ) непрерывна в
причем
f ( x ) непрерывна в
![]() то
то
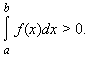
|
f ( x )| интегрируема на [ a ; b ], причем
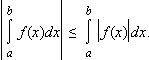
Если
на отрезке [ a ; b ] m ≤ f
( x ) ≤ M , то
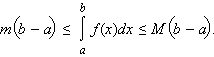
Билет34:
Пусть f (x) произвольная непрерывная на отрезке [a, b] функция и пусть F (x) какая-нибудь её первообразная. Разобьём отрезок [a, b] на n частей и составим разность F ( b ) - F ( a )значений первообразной на концах интервала [a, b]. Эта разность равна сумме разностей, составленных для каждого отрезка разбиения, ……….. По теореме Лагранжа о "конечном приращении" имеем …………. поэтому …………. Это равенство является точным при любом разбиении отрезка [a, b], но оно справедливо лишь при определённом выборе на каждом отрезке разбиения точек c1 < c2 < … < cn, которые предписывается теоремой Лагранжа. Если размеры всех отрезков разбиения а = х0, x1], [х1, x2],…, [х n - 1, b] будут становиться всё меньше и меньше, то сумма ………… будет являться суммой возрастающего числа стремящихся к нулю слагаемых. Если равенство …………. верно всегда, то оно верно и в пределе: ………… Полученное равенство замечательно тем, что оно справедливо не только при каком-то частном выборе точек c1 < c2 < … < cn по одной на отрезках деления [а = х0, x1], [х1, x2],…, [х n - 1, b] как это предписывается теоремой Лагранжа, но при всяком выборе точек ξ 1 < ξ 2, <… < ξ n по одной на отрезках деления [а = х0, x1], [х1, x2],…,[хn - 1, b]: ………….. Последнее соотношение является замечательным правилом суммирования бесконечно малых, открытых Лейбницем и Ньютоном: для отыскания предела суммы бесконечно малых ………….. когда все отрезки, на которые разбит отрезок [a, b], безгранично умаляются, необходимо выполнить два действия: 1) постараться отыскать конечным образом какую-нибудь первообразную F(х) для функции f (x); 2) найдя первообразную F(х), составить разность F(b) - F(a) её значений на концах основного отрезка [a, b]. Эта разность и есть искомый предел. Сопоставляя это правило с определением определённого интеграла, получим формулу Ньютона—Лейбница ………………………..
