Билет 1:

Кинематика поступательного движения

При поступательном движении тела все точки тела движутся одинаково, и, вместо того чтобы рассматривать движение каждой точки тела, можно рассматривать движение только одной его точки.

Основные характеристики движения материальной точки: траектория движения, перемещение точки, пройденный ею путь, координаты, скорость и ускорение.

Линию, по которой движется материальная точка в пространстве, называют траекторией.

Перемещением материальной точки за некоторый промежуток времени называется вектор перемещения ∆r=r-r0, направленный от положения точки в начальный момент времени к ее положению в конечный момент.

Скорость материальной точки представляет собой вектор, характеризующий направление и быстроту перемещения материальной точки относительно тела отсчета. Вектор ускорения характеризует быстроту и направление изменения скорости материальной точки относительно тела отсчета. 

Система отсчёта — это совокупность точки отсчёта, системы координат и системы отсчёта времени, связанных с этой точкой, по отношению к которой изучается движение (или равновесие) каких-либо других материальных точек или тел^[1].

Математически движение тела (или материальной точки) по отношению к выбранной системе отсчёта описывается уравнениями, которые устанавливают, как изменяются с течением времени t координаты, определяющие положение тела (точки) в этой системе отсчёта. Эти уравнения называются уравнениями движения. Например, в декартовых координатах х, y, z движение точки определяется уравнениями x = f₁(t), y = f₂(t), z = f₃(t).

В современной физике любое движение является относительным, и движение тела следует рассматривать лишь по отношению к какому-либо другому телу (телу отсчёта) или системе тел. Нельзя указать, например, как движется Луна вообще, можно лишь определить её движение, например, по отношению к Земле, Солнцу, звёздам и т. п

Траекто́рия материа́льной то́чки  — линия в трёхмерном пространстве, представляющая собоймножество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве.^[1]. Существенно, что понятие о траектории имеет физический смысл даже при отсутствии какого-либо по ней движения. Кроме того, и при наличии движущегося по ней объекта, траектория сама по себе не может ничего дать в отношении причин движения, то есть о действующих силах.^[2]

Описание траектории

Принято описывать траекторию материальной точки при помощи радиус-вектора, направление, длина и начальная точка которого зависят от времени. При этом кривая, описываемая концом радиус-вектора в пространстве может быть представлена в виде сопряжённых дуг различной кривизны, находящихся в общем случае в пересекающихся плоскостях. При этом кривизна каждой дуги определяется её радиусом кривизны, направленном к дуге из мгновенного центра поворота, находящегося в той же плоскости, что и сама дуга. При том прямая линия рассматривается как предельный случай кривой, радиус кривизны которой может считаться равным бесконечности.И потому траектория в общем случае может быть представлена как совокупность сопряжённых дуг.

Существенно, что форма траектории зависит от системы отсчёта, избранной для описания движения материальной точки. Так прямолинейное движение в инерциальной системе в общем случае будет параболическим в равномерно ускоряющейся системе отсчёта.

Перемещением тела   называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением.Перемещение есть векторная величина.

Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.

Если движение тела рассматривать в течение достаточно короткого промежутка времени, то вектор перемещения окажется направленным по касательной к траектории в данной точке, а его длина будет равна пройденному пути.

В случае достаточно малого промежутка времени Δt пройденный телом путь Δl почти совпадает с модулем вектора перемещения   При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.1.2).

Рисунок 1.1.2.

Пройденный путь l и векторперемещения   при криволинейномдвижении тела. a и b – начальная и конечная точки пути

Билет 7:

Центр масс

[ Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Центр тяжести (значения).

Центр масс (центр ине́рции; барице́нтр от др.-греч. βαρύς «тяжёлый» и κέντρον «центр») в механике — это геометрическая точка, характеризующая движение тела или системы частиц как целого.

[Определение

Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом:

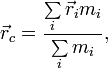
где

 — радиус-вектор центра масс,

 — радиус-вектор i-й точки системы,

 — масса i-й точки.

Для случая непрерывного распределения масс:

где:

 — суммарная масса системы,

 — объём,

 — плотность.

Центр масс, таким образом, характеризует распределение массы по телу или системе частиц.

[править]Центры масс однородных фигур

У отрезка — середина.

У многоугольников (как сплошных плоских фигур, так и каркасов):

У параллелограмма — пересечение диагоналей.

У треугольника — точка пересечения медиан (центроид).

У правильного многоугольника — центр поворотной симметрии.[править]В механике

Понятие центра масс широко используется в физике.

Движение твёрдого тела можно рассматривать как суперпозицию движения центра масс и вращательного движения тела вокруг его центра масс. Центр масс при этом движется так же, как двигалось бы тело с такой же массой, но бесконечно малыми размерами (материальная точка). Последнее означает, в частности, что для описания этого движения применимы все законы Ньютона. Во многих случаях можно вообще не учитывать размеры и форму тела и рассматривать только движение его центра масс.

Часто бывает удобно рассматривать движение замкнутой системы в системе отсчёта, связанной с центром масс. Такая система отсчёта называется системой центра масс (Ц-система), или системой центра инерции. В ней полный импульс замкнутой системы всегда остаётся равным нулю, что позволяет упростить уравнения её движения.

[править]Центр масс в релятивистской механике

В случае высоких скоростей (порядка скорости света) (например, в физике элементарных частиц) для описания динамики системы применяется аппарат СТО. В релятивистской механике (СТО) понятия центра масс и системы центра масс также являются важнейшими понятиями, однако, определение понятия меняется:

где

 — радиус-вектор центра масс,

 — радиус-вектор i-й частицы системы,

 — полная энергия i-й частицы.

Во избежание ошибок следует понимать, что в СТО центр масс характеризуется не распределением массы, а распределением энергии. В курсе теоретической физики Ландау и Лившица предпочтение отдается термину «центр инерции». В западной литературе по элементарным частицам применяется термин «центр масс» (center-of-mass). Оба термина эквивалентны.

Центр тяжести

Центр масс тела не следует путать с центром тяжести!

Центром тяжести тела называется точка, относительно которой суммарный момент сил тяжести, действующих на систему, равен нулю. Например, в системе, состоящей из двух одинаковых масс, соединённых несгибаемым стержнем, и помещённой в неоднородное гравитационное поле (например, планеты), центр масс будет находиться в середине стержня, в то время как центр тяжести системы будет смещён к тому концу стержня, который находится ближе к планете (ибо вес массы P = m·g зависит от параметра гравитационного поля g), и, вообще говоря, даже расположен вне стержня.

В постоянном параллельном (однородном) гравитационном поле центр тяжести всегда совпадает с центром масс. Поэтому на практике эти два центра почти совпадают (так как внешнее гравитационное поле в некосмических задачах может считаться постоянным в пределах объёма тела).

По этой же причине понятия центр масс и центр тяжести совпадают при использовании этих терминов в геометрии, статике и тому подобных областях, где применение его по сравнению с физикой можно назвать метафорическим и где неявно предполагается ситуация их эквивалентности (так как реального гравитационного поля нет и не имеет смысла учёт его неоднородности). В этих применениях традиционно оба термина синонимичны, и нередко второй предпочитается просто в силу того, что он более старый.

Формула Циолковского

Формула Циолковского определяет скорость, которую развивает летательный аппарат под воздействием тяги ракетного двигателя, неизменной по направлению, при отсутствии всех других сил. Эта скорость называется характеристической.

,

где:

V — конечная (после выработки всего топлива) скорость летательного аппарата;

I — удельный импульс ракетного двигателя (отношение тяги двигателя к секундному расходу массы топлива);

M₁ — начальная масса летательного аппарата (полезная нагрузка + конструкция аппарата + топливо).

M₂ — конечная масса летательного аппарата (полезная нагрузка + конструкция);

Эта формула была выведена К. Э. Циолковским в рукописи «Ракета» 10 мая 1897 года.^[1]

Однако первыми уравнение движения тела с переменной массой решили английские исследователи У. Мур, а также П. Г. Тэйт и У. Дж. Стил из Кембриджского университетасоответственно в 1810—1811 гг. и в 1856 году.

Формула Циолковского может быть получена путём интегрирования дифференциального уравнения Мещерского для материальной точки переменной массы:

,

в котором m — масса точки;

V — скорость точки;

u — относительная скорость, с которой движется отделяющаяся от точки часть её массы. Для ракетного двигателя эта величина и составляет его удельный импульс I^[2]

Для многоступенчатой ракеты конечная скорость рассчитывается как сумма скоростей, полученных по формуле Циолковского отдельно для каждой ступени, причем при расчёте характеристической скорости каждой ступени к её начальной и конечной массе добавляется суммарная начальная масса всех последующих ступеней.

Введем обозначения:

M1_i — масса заправленной i-ой ступени ракеты;

M2_i — масса i-ой ступени без топлива;

I_i — удельный импульс двигателя i-ой ступени;

M₀ — масса полезной нагрузки;

N — число ступеней ракеты.

Тогда формула Циолковского для многоступенчатой ракеты может быть записана в следующем ви

Билет 9: Динамика вращательного движения

Пусть твёрдое тело вращается относительно неподвижной оси. Тогда уравнения движения значительно упрощаются.

Действительно:

1)   - кинетический момент.

Во вращательном движении   , поэтому   .

Но из   .

Итак:

 ,

где   - момент инерции относительно оси вращения Z.

Уравнение движения:

 окончательно,   .

2) Кинетическая энергия:

 .

Итак,

 .

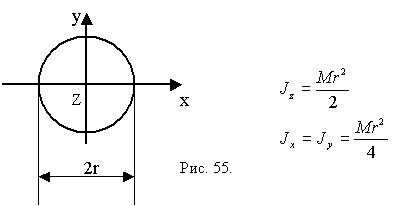
Моменты инерции некоторых тел (рис. 55):

1 Тонкий прямой стержень

2. Тонкое кольцо (обод)

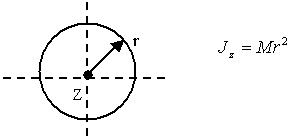
3. Сплошной диск

 

Пример:

 

Q – вес обода. P – вес груза. Найти a – ускорения груза Р.

 

Рис.56.

 

По теореме об изменении кинетического момента системы:

 

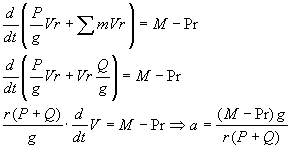
Таким образом, при вращательном движении твёрдого тела удобно пользоваться соотношениями теоремы об изменении кинетического момента системы.

Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения СИ: кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.

Осевой момент инерции

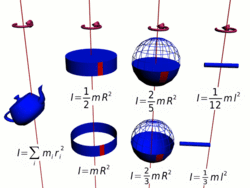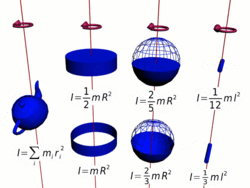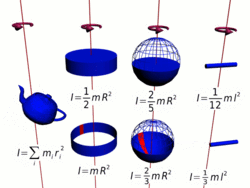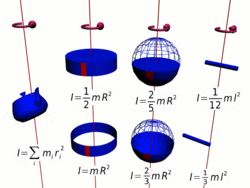
Осевые моменты инерции некоторых тел.

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

где:

m_i — масса i-й точки,

r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как массатела является мерой его инертности в поступательном движении.

,

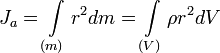где:

dm = ρdV — масса малого элемента объёма тела dV,

ρ — плотность,

r — расстояние от элемента dV до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

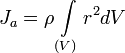
[править]Теорема Гюйгенса-Штейнера

Основная статья: Теорема Штейнера

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

Если   — момент инерции тела относительно оси, проходящей через центр масс тела, то момент инерции относительно параллельной оси, расположенной на расстоянии   от неё, равен

,

где   — полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

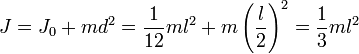
Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения
Тело	Описание	Положение оси a	Момент инерции Ja
	Материальная точка массы m	На расстоянии r от точки, неподвижная
	Полый тонкостенный цилиндр или кольцо радиуса r и массы m	Ось цилиндра
	Сплошной цилиндр или диск радиуса r и массы m	Ось цилиндра
	Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1	Ось цилиндра
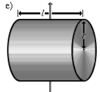
	Сплошной цилиндр длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс
	Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс
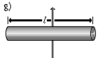
	Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его центр масс
	Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец
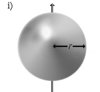
	Тонкостенная сфера радиуса r и массы m	Ось проходит через центр сферы
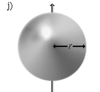
	Шар радиуса r и массы m	Ось проходит через центр шара
	Конус радиуса r и массы m	Ось конуса
	Равнобедренный треугольник с высотой h, основанием a и массой m	Ось перпендикулярна плоскости треугольника и проходит через вершну
	Правильный треугольник со стороной a и массой m	Ось перпендикулярна плоскости треугольника и проходит через центр масс
	Квадрат со стороной a и массой m	Ось перпендикулярна плоскости квадрата и проходит через центр масс

Билет 10:

Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).

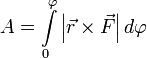 или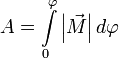 

Формула момента рычага

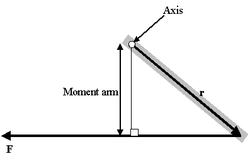
Момент рычага

Очень интересен особый случай, представляемый как определение момента силы в поле:

 = МОМЕНТ_РЫЧАГА * СИЛА

Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален

 = РАССТОЯНИЕ_ДО_ЦЕНТРА * СИЛА

Сила под углом

Если сила F направлена под углом θ к рычагу r, то M = r*F*sinθ, где θ это угол между рычагом и приложенной силой

Статическое равновесие

Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении ΣM=0.

[править]Момент силы как функция от времени

Момент силы — производная по времени от момента импульса,

 ,

где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.

 ,

То есть если I постоянная, то

 ,

где α — угловое ускорение, измеряемое в радианах в секунду за секунду.

[править]Отношение между моментом силы и мощностью

Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.

 = МОМЕНТ_СИЛЫ * УГЛОВАЯ_СКОРОСТЬ

В системе СИ мощность   измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.

Отношение между моментом силы и работой

 = МОМЕНТ_СИЛЫ * УГОЛ

В системе СИ работа   измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в радианах.

Обычно известна угловая скорость   в радианах в секунду и время действия МОМЕНТА  .

Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:

 = МОМЕНТ_СИЛЫ *   * 

Момент силы относительно точки

Если имеется материальная точка  , к которой приложена сила  , то момент силы относительно точки   равен векторному произведению радиус-вектора  , соединяющий точки O и O_F, на вектор силы  :

.

Момент силы относительно оси

Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.

Единицы измерения

Момент силы измеряется в ньютон-метрах. 1 Н·м — момент силы, который производит сила 1 Н на рычаг длиной 1 м. Сила приложена к концу рычага и направлена перпендикулярно ему.

Измерение момента

На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM, Lorenz (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).