Элементы теории матричных игр

1.В обычных задачах определенного типа нахождение экстремума какой-либо функции выполнялось однозначно по определенным правилам. На практике встречаются задачи, в которых результат зависит от обстоятельств, которые могут происходить с определенной вероятностью: шахматы, шашки, азартные игры, военные операции. Обычно в таких задачах участвуют две стороны, которых называют игроками. В соответствии с правилами игры каждый игрок выполняет определенные действия. При этом каждый старается эти действия выполнять так, чтобы получить наибольшую выгоду.

Эти действия называют стратегии игроков. Результатом игры будет являться некоторая величина, которая называется выигрышем/проигрышем игрока. Если каждый из игроков имеет конечное число стратегий, то игра называется конечной. Интересы каждого из игроков противоположны.

2.Матричная игра двух лиц с нулевой суммой

Играют два лица. Выигрыш одного = проигрышу другого

- выигрыш первого,

- проигрыш второго

Пусть 1ый игрок имеет стратегий, а 2ой стратегий.

Результатом игры при выборе соответствующей стратегии будет некоторая величина = выигрышу первого игрока (проигрышу второго) при выборе первым i-ой, а вторым j-ой стратегии.

Все выигрыши обычно записываются в виде платежной матрицы

Зная платежную матрицу каждый из игроков должен получить максимальный выигрыш первый и минимальный второй.

Обычно платежная матрица записывается в виде матрицы выигрышей первого игрока. Первый игрок должен выбирать свои стратегии так, чтобы получить наибольший выигрыш независимо от действий второго, а второй независимо от действий первого. Соответствующие стратегии в этом случае называются оптимальными.

Пример:

Первый игрок должен действовать по правилу: .

Т.е. первый игрок находит сначала наименьший элемент в каждой строке и из этих наименьших элементов выбирает наибольшее число и строка, в которой это достигается – оптимальная.

Второй игрок должен действовать по правилу: .

Т.е. второй игрок в каждом столбце выбирает наибольший элемент и из этих элементов выбирает наименьший, и столбец (стратегия) будет оптимальной для второго игрока.

Числа и называются соответственно

- нижняя цена игры

- верхняя цена игры

- цена игры

В примере . Точка, для которой называется седловой точкой игровой матрицы. Эта число является наименьшей в строке и наибольшей в столбце для данной матрицы. Если эта точка есть, то она и определяет оптимальный выбор стратегии игроков.

Удобно записывать процедуры выбора игроками соответствующей строки (столбца) игровой матрицы, т.е. его чистые стратегии в виде вектора:

- для первого игрока

- для второго игрока,

где одна из координат вектора равна 1, а остальные координаты равны 0.

В этом случае в данном примере оптимальные стратегии игроков запишутся:

- для первого игрока,

- для второго игрока

Если седловой точки нет, то решение игры в чистых стратегиях невозможно. В этом случае решение находим в смешанных стратегиях.

3.Смешанные стратегии игроков

Смешанной стратегией первого игрока называется набор чисел , удовлетворяющих условиям:

1)

2)

т.е. смешанная стратегия первого игрока – распределение вероятностей выбора первым игроком соответствующей строки матрицы .

Смешанной стратегией второго игрока называется набор чисел , удовлетворяющих условиям:

1)

2)

т.е. смешанная стратегия второго игрока – распределение вероятностей выбора вторым игроком столбцов платежной матрицы

Результатом игры в смешанных стратегиях будет математическое ожидание выигрыша (проигрыша) первого (второго) игрока:

Это число удовлетворяет следующим условиям:

1. Если ко всем элементам матрицы А прибавить постоянное число С, то М.О. выигрыша (цена игры) увеличится на это число.

- м.о. выигрыша 1го игрока (проигрыша 2го игрока) в стратегиях и . С – постоянное число.

Р ассмотрим

т.к. =>

Из этого свойства получаем важное следствие: прибавив к элементам данной матрицы соответствующее число С, можно всегда добиться того, что математическое ожидание будет положительным, т.е. всегда

2. Если все элементы матрицы умножить на , то

Из 1 и 2 следует линейность м.о. выигрыша игрока 1

3.Оптимальные смешанные стратегии игроков

Оптимальной стратегией первого (второго) игрока называется такая смешанная стратегия, при которой он получает наибольший (наименьший) выигрыш н/з от выбора стратегии второго игрока.

Результат игры в смешанных стратегиях всегда характеризуется м.о. выигрыша , то для оптимальных смешанных стратегий будут выполнятся неравенства (их определения):

- оптимальные стратегии игроков, то: (1)

Существование оптимальных стратегий

Теорема Неймана: Любая матричная игра двух лиц с 0 суммой для каждого из игроков имеет оптимальные стратегии

Возникает задача о нахождении этих оптимальных стратегий.

5.Нахождение оптимальных стратегий игроков

Пусть игра определяется матрицей - выигрыш первого игрока, где все =>

Нахождение оптимальных стратегий сводится к решению пары двойственных задач линейного программирования следующим образом:

1. Нахождение оптимальной стратегии второго игрока

Рассмотрим левую часть неравенства (1)

, (2)

Выберем вида , где на i-ом месте стоит 1, тогда неравенство (2) перепишется (3)

Обозначим , рассмотрим функцию =>

Неравенство (3) перепишется: (4)

Второй игрок выбирает стратегию так, чтобы было наименьшим, а значит наибольшим. Поэтому для нахождения оптимальной смешанной стратегии , получим следующую задачу ЛП:

(I)

2. Нахождение оптимальной стратегии 1го игрока

Рассмотрим правую часть неравенства (1)

(2’)

Выберем вида , где на j-ом месте стоит 1, тогда неравенство (2’) перепишется

(3’)

Обозначим , рассмотрим функцию: =>

Неравенство (3’) перепишется:

(4)

Поэтому для нахождения оптимальной смешанной стратегии , получим следующую задачу ЛП:

(II)

Оказалось, что для нахождения оптимальных стратегий нужно решить пару двойственных задач линейного программирования, которые в совмещенной таблице записываются следующим образом:

			…
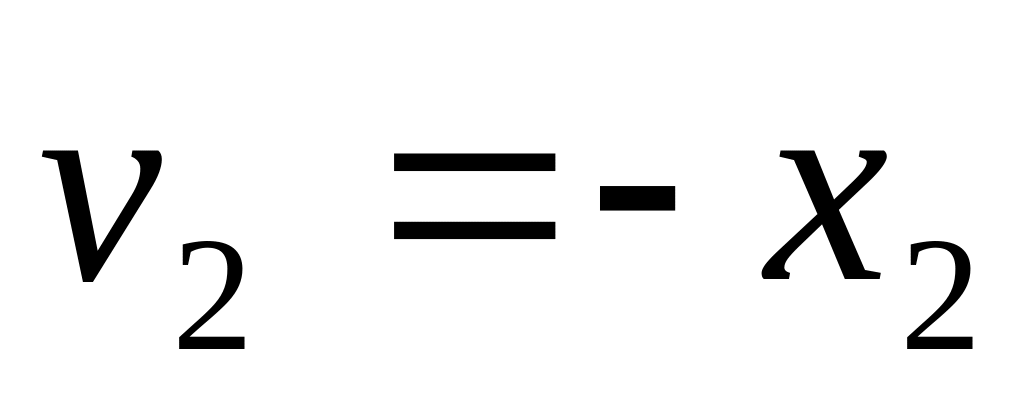
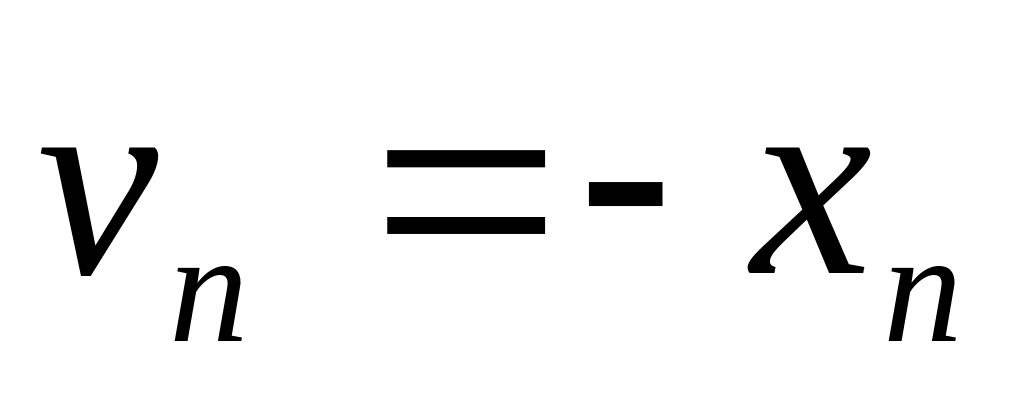
			…		1
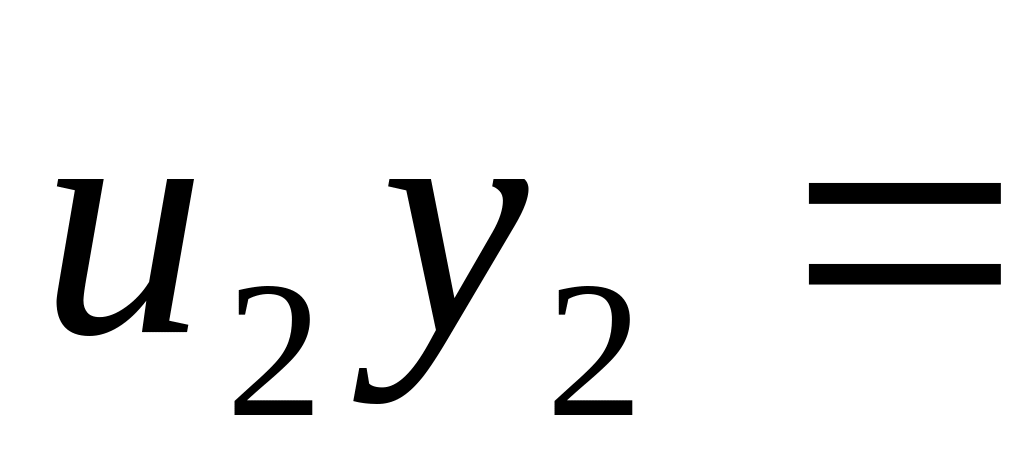
			…		1
…	…	…	…		1
			…		1
	-1	-1	…	-1	0

Итак, задача нахождения - оптимальных стратегий игроков сведена к решению пары двойственных задач линейного программирования. Решение игровой задачи будет определяться формулами:

1. Решив задачу линейного программирования получим:

, при

, при ,

причем

=

2. ,

Из этих формул получаем решение игровой задачи, т.е. V – цена игры, - оптимальные стратегии игроков:

- цена игры. (1)

, , j=1,2,…,k

Пример 1: Найти оптимальные стратегии игроков для матрицы А:

Составим совмещенную таблицу

		3		12		1
		1		0		1
		9		0		1
		1		2		1
		-1		-1		0

	-3/9	12	6/9
	-1/9	0	8/9
	1/9	0	1/9
	-1/9	2	8/9
	1/9	-1	1/9

	3/(9*12)	1/12	6/(9*12)
		0	8/9
		0	1/9
		2/12	84/(9∙2)
	1/12	1/12	18/(9∙12)

, ,

Оптимальные стратегии и цены игры находим по формулам:

, , ,

, .

Проверка:

6.Порядок решения матричной игры

1. Освобождаемся от отрицательных элементов матрицы , путем прибавления соответствующего постоянного числа , получим матрицу

где

2. Решим пару двойственных задач ЛП, записанных в соответствующей таблице

			…
					1
					1
…					1
					1
	-1	-1	…	-1	0

3. Оптимальные стратегии игры находятся по формулам

   • , где

   • 

   • 

7.Упрощение матрицы игры

Если все элементы какой-либо строки (столбца) матрицы больше соответствующих элементов другой строки (столбца), то говорят, что столбец с большими элементами доминирует над столбцом с меньшими (строкой).

Первый игрок старается получить наибольший выигрыш, поэтому строки с меньшими элементами он будет выбирать с 0 вероятностью, поэтому эти строки можно вычеркнуть, приписав им вероятность выбора равную 0.

Второй игрок желает получить минимальный проигрыш, поэтому столбцы с большими элементами он выбирать не будет, т.е. он выбирает их с вероятностью 0, т.е. их тоже можно вычеркнуть, приписав этим столбцам вероятность выбора равную 0.

Окончательно матрица содержит несравнимые строки и столбцы, и задача решается обычным образом, сохраняя первоначальную нумерацию строк и столбцов.

Пример 2: Найти оптимальные стратегии игроков для матрицы:

В этой матрице вторая строка доминирует над первой и четвёртой, поэтому эти строки игрок будет выбирать с нулевыми вероятностями, т.е. и . Вычеркнув эти строки из А получим матрицу :

В этой матрице строки и столбцы несравнимы и дальнейшее упрощение невозможно. Согласно алгоритму решения прибавим к элементам этой матрицы число , чтобы в новой матрице все элементы были неотрицательны:

Решая игру с матрицей , последовательно получим:

						3			6			1
						6			0			1
						-1			-1			0

	-1/2	6	1/2
	1/6	0	1/6
	1/2	-1	1/6

	-1/12	1/6	1/12
	1/4	0	1/6
	1/12	1/6	1/4

Из последней таблицы получаем решение пары двойственных задач линейного программирования:

при , и при ,

Отсюда по формулам (1) получим решение игры:

, тогда

, тогда ; ;

, тогда ;

Окончательно получаем решение задачи:

; - оптимальные стратегии первого и второго игроков,

- цена игры.

Проверка:

8.Графическое решение матричной игры

Если матрица игры имеет размеры или , т.е. содержит 2 строки и n-столбцов или m-строк и 2 столбца, то в этом случае можно найти решение таких игр графическим способом.

Пусть матрица игры , т.е. первый игрок, имеет две стратегии, которые он может выбрать с вероятностями и ., причем (1).

1)Будем находить м.о. выигрышей первого игрока при различных чистых стратегиях второго. Этих стратегий всего n: , .

Тогда м.о. выигрыша первого игрока будет иметь вид:

Т.е. (2) или учитывая (1) получаем:

, где .

Окончательно: , , (3)

Геометрически уравнение (3) есть уравнение прямой линии в системе , а при получаем семейство прямых линий. Т.к. число этих прямых конечно, то можно определить нижнюю границу этого семейства – огибающую, которая представляет собой ломаную линию, ограничивающую снизу выигрыши первого игрока.

На этой огибающей находим наивысшую точку М . Ордината этой точки есть наибольший выигрыш первого игрока при любых стратегиях второго игрока, т.е. цену игры V, а абсцисса p₁* есть одна из координат оптимальной стратегии первого игрока. Окончательно получим: