
- •Элементы теории игр Жордановы исключения
- •Элементы теории матричных игр
- •- Оптимальная стратегия первого игрока
- •Находим оптимальные стратегии второго игрока по матрице
- •- Оптимальная стратегия второго игрока b.
- •Для матрицы b решаем соответствующую пару двойственных задач линейного программирования:
- •11. Графическое решение биматричной игры
- •Литература.
- Оптимальная стратегия первого игрока
- цена игры
2) При нахождении
оптимальной стратегии второго игрока
поступают следующим образом. Известна
цена игры
- ордината точки
![]() ,
как точки пересечения двух прямых.
Нахождение стратегии
,
как точки пересечения двух прямых.
Нахождение стратегии
![]() определяется этой точкой
.
Поэтому второй игрок должен выбрать
такие чистые стратегии (столбцы), которым
будут соответствовать две
прямые,
проходящие через
.
Остальные столбцы выбирают с вероятностью
0. Выбирая эти столбцы, второй игрок
получит минимальный проигрыш при любой
стратегии первого игрока.
определяется этой точкой
.
Поэтому второй игрок должен выбрать
такие чистые стратегии (столбцы), которым
будут соответствовать две
прямые,
проходящие через
.
Остальные столбцы выбирают с вероятностью
0. Выбирая эти столбцы, второй игрок
получит минимальный проигрыш при любой
стратегии первого игрока.
Пример 3: Найти оптимальные стратегии игроков для матрицы:
![]()

![]()
Находим М.о 1го игрока:
![]()
![]()
![]()
Огибающая
 показывает м.о.
показывает м.о.
Выигрышей первого игрока при любых
стратегиях второго игрока.
Точка
![]() определяет оптимальную
определяет оптимальную
стратегию
![]() и цену игры
и цену игры
![]()
![]()
![]()
![]()
![]()
Нахождение оптимальной стратегии 2го игрока:
точка
![]() получается как пересечение прямых
получается как пересечение прямых
![]() и
и
![]() ,
которые соответствуют стратегиям 2го
игрока
,
которые соответствуют стратегиям 2го
игрока
![]() и
и
![]() ,
поэтому он должен выбирать стратегии
и
,
а
,
поэтому он должен выбирать стратегии
и
,
а
![]() и
и
![]() =0.
При таких условиях находим цену игры
при любых стратегиях 1го игрока:
=0.
При таких условиях находим цену игры
при любых стратегиях 1го игрока:
![]()
![]()
![]()
![]()
![]()
Аналогично
рассмотрим случай, когда игровая матрица
![]() ,
т.е. второй игрок имеет две стратегии,
которые он может выбирать с вероятностями
и
.,
причем
,
т.е. второй игрок имеет две стратегии,
которые он может выбирать с вероятностями
и
.,
причем
![]() (1).
(1).
Как и раньше будем находить м.о. проигрыша, но уже второго игрока при различных чистых стратегиях первого игрока. Этих стратегий будет всего m;
![]() ,
,
![]() .
.
Тогда м.о. выигрыша первого игрока будет иметь вид:

Т.е.
![]()
учитывая (1) получаем:
![]() (2),
(2),
Обозначим
![]() ,
,
![]() ,
тогда равенство
(2) окончательно перепишется:
,
тогда равенство
(2) окончательно перепишется:
![]() ,
,
,
,
![]() (3)
(3)
Геометрически
уравнение (3) есть уравнение прямой
линии в системе
![]() ,
а при
получаем семейство прямых линий,
характеризующих м.о. проигрышей второго
игрока при различных стратегиях первого
игрока. Графически это представлено
на рисунке:
,
а при
получаем семейство прямых линий,
характеризующих м.о. проигрышей второго
игрока при различных стратегиях первого
игрока. Графически это представлено
на рисунке:

Для этого семейства
прямых определим верхнюю границу
проигрышей второго игрока – огибающую,
которая представляет ломаную линию.
На этой линии находим нижнюю точку М![]() .
Ордината этой точки
.
Ордината этой точки
![]() есть
наименьший проигрыш второго игрока
при любых стратегиях первого игрока.
есть
наименьший проигрыш второго игрока
при любых стратегиях первого игрока.
Окончательно получим:
![]() -
оптимальная стратегия второго игрока
-
оптимальная стратегия второго игрока
- цена игры
Для нахождения оптимальной стратегии первого игрока рассуждают, как и в случае с матрицей .
Точка
есть точка пересечения двух прямым,
которые соответствуют двум чистым
стратегиям
![]() и
и
![]() первого игрока. Поэтому, выбирая эти
стратегии, если
первого игрока. Поэтому, выбирая эти
стратегии, если
![]() ,
а остальные свои стратегии с нулевой
вероятностью, первый игрок получит
выигрыш
,
а остальные свои стратегии с нулевой
вероятностью, первый игрок получит
выигрыш
![]() ,
при любых стратегиях второго игрока.
,
при любых стратегиях второго игрока.
Пример 4: Найти оптимальные стратегии игроков для матрицы:

![]()
1)Находим М.о проигрыша 2го игрока, при выборе его 1 стратегии (строки)
![]() - прямая проигрышей
- прямая проигрышей
2)
![]()
3)
![]()
4)
![]()
Л оманая
огибает
проигрыши 2го
оманая
огибает
проигрыши 2го
Игрока сверху, на этой огибающей
Нижней точкой
будет точка
![]()
Находим координаты
этой точки:
![]()
![]()
![]()
![]() - оптимальная
- оптимальная
стратегия 2го
игрока.
![]() - цена
- цена
игры. Нахождение : известна цена игры
![]() ,
она определяется точкой
,
поэтому
,
она определяется точкой
,
поэтому
1ый игрок должен выбрать такие
стратегии (строки), которым будут
соответствовать прямые, проходящие ч/з
точки
,
т.е. выбирать стратегии
и
![]() ,
т.к. остальные строки выбираются с 0
вероятностью. Выбирая эти строки, 1ый
игрок
,
т.к. остальные строки выбираются с 0
вероятностью. Выбирая эти строки, 1ый
игрок
получит максимальный выигрыш равный
при любой стратегии 2го игрока.
![]()
![]()
![]()
![]()
![]()
Выберем
![]() - оптимальная стратегия 2го игрока
- оптимальная стратегия 2го игрока
![]() получили тождество
=> для нахождения оптимальной стратегии
1го игрока нужно выбирать любые стратегии,
кроме его оптимальных, т.к. в этом случае
получаем тождество.
получили тождество
=> для нахождения оптимальной стратегии
1го игрока нужно выбирать любые стратегии,
кроме его оптимальных, т.к. в этом случае
получаем тождество.
9.Эквивалентная запись определения оптимальных стратегий матричной игры
По определению оптимальной стратегии матричной игры должны удовлетворять следующему неравенству:
(1)
Рассмотрим эти неравенства отдельно:
1)![]() решая это неравенство найдем оптимальную
стратегию
второго игрока по матрице
как прямую
задачу ЛП на максимум.
решая это неравенство найдем оптимальную
стратегию
второго игрока по матрице
как прямую
задачу ЛП на максимум.
2)
![]() решая это неравенство найдем оптимальную
стратегию
первого игрока по матрице
,
как двойственную
задачу ЛП на минимум.
решая это неравенство найдем оптимальную
стратегию
первого игрока по матрице
,
как двойственную
задачу ЛП на минимум.
Т.е. нахождение , как это было показано ранее, сводится к решению пары взаимно двойственных задач ЛП по данной игровой матрице .
Неравенство (1) можно эквивалентным образом переписать иначе.
Первое неравенство оставим прежним, т.е.:
![]() (2)
(2)
Второе перепишем так:
![]()
![]()
Умножим обе части на -1:
![]()
Обозначим
![]()
![]() , тогда предыдущее неравенство запишется:
, тогда предыдущее неравенство запишется:
![]()
В новых обозначениях неравенство (1) равносильно перепишется системой:
1)
![]() ,
где
(2)
,
где
(2)
10.Биматричные игры
В конкретных
ситуациях участвуют 2 игрока
и
![]() .
Выигрыши игрока
определяются матрицей
,
а выигрыши игрока
определяются матрицей
.
Выигрыши игрока
определяются матрицей
,
а выигрыши игрока
определяются матрицей
![]() (того
же размера). Игра происходит следующим
образом: игрок
выбирает стратегию i
(строку), а игрок
стратегию j
(столбец), тогда игрок
получает выигрыш
,
а игрок
-
(того
же размера). Игра происходит следующим
образом: игрок
выбирает стратегию i
(строку), а игрок
стратегию j
(столбец), тогда игрок
получает выигрыш
,
а игрок
-
![]() .
.
Биматричной игрой 2х лиц и называется игра, определяемая матрицами выигрышей для 1го игрока и для 2го игрока.
Оптимальными
стратегиями игроков называются
стратегии
для
,
для
,
удовлетворяющие неравенствам:
![]() ,
,
![]() .
.
Из полученного определения получаем следующий порядок нахождения оптимальных стратегий:
По матрице из неравенства находим оптимальную стратегию второго игрока как прямую задачу ЛП
По неравенству находим оптимальную стратегию игрока по матрице как решение двойственной задачи ЛП.
Схема решения биматричной игры:
-
…
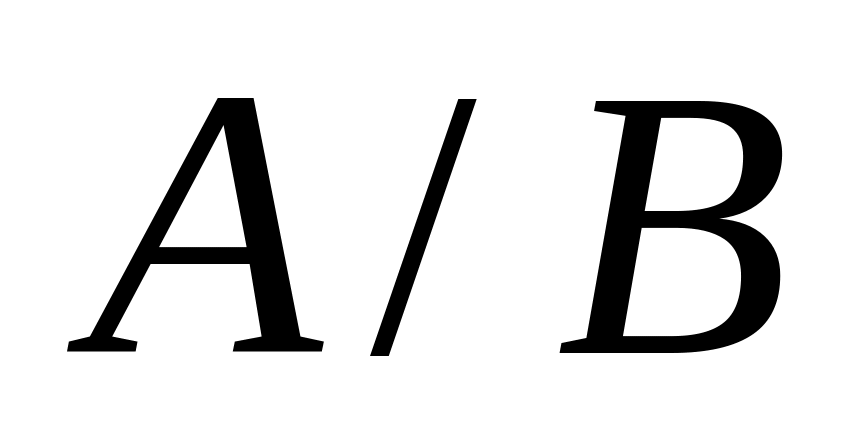
1
1
…
1
1
-1
-1
…
-1
0

|
|
|
|
… |
|
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
1 |
|||||||||||||
|
|
1 |
||||||||||||||
|
… |
1 |
||||||||||||||
|
|
1 |
||||||||||||||
|
|
-1 |
-1 |
… |
-1 |
0 |
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|||||||||||||
|
|
|
||||||||||||||
|
|
|
||||||||||||||
|
|
|
||||||||||||||
|
|
|
|
|||||||||||||
|
|
|
… |
|
|
|
|
1 |
|||
|
1 |
||||
… |
1 |
||||
|
1 |
||||
|
-1 |
-1 |
… |
-1 |
0 |
![]() ,
по матрице
,
,
по матрице
,
а игрока по формуле:
![]() ,
по матрице
.
,
по матрице
.
Цена игры находится по формулам:
![]() - цена игры первого
игрока
- цена игры первого
игрока
![]() - цена игры второго
игрока
- цена игры второго
игрока
Пример 5: Найти решение биматричной игры:
![]()
![]()
