Короткая форма интерполяционной формулы Ньютона

В случае равноудаленных центров интерполяции, находящихся на единичном расстоянии друг от друга, справедлива формула:

где   — обобщенные на область действительных чисел биномиальные коэффициенты.

Прямая интерполяционная формула Ньютона

 где  , а выражения вида Δ^ky_i — конечные разности.

Обратная интерполяционная формула Ньютона

 где 

Билет37. Сплайновая интерполяцияИнтерполяция сплайнами. Пусть отрезок [a,b] разбит точками на n частичных отрезков . Сплайном степени m называется функция , обладающая следующими свойствами:

1) функция непрерывна на отрезке [a,b] вместе со своими производными до некоторого порядка  p.

2) на каждом частичном отрезке функция совпадает с некоторым алгебраическим многочленом степени m.

Разность m-p между степенью сплайна и наивысшим порядком непрерывной на отрезке [a,b] производной называют дефектом сплайна. Кусочно-линейная функция является сплайном первой степени с дефектом, равным единице. Действительно, на отрезке [a,b] сама функция (нулевая производная) непрерывна. В то же время на каждом частичном отрезке совпадает с некоторым многочленом первой степени.

Наиболее широкое распространение получили сплайны 3 степени (кубические сплайны) с дефектом равным 1 или 2.

Билет № 38.Методы решения нелинейных уравнений

Методы решения нелинейных уравнений делятся на прямые и итерационные.

Прямые методы позволяют записать корни в виде конечного соотношения (формулы).

В большинстве случаев уравнения приходится решать, используя итерационные методы

В результате итераций находится последовательность приближенных значений корня: x1, x2, x3,……., xn.

Этапы

1. Отделение корней, т.е. установление возможных промежутков (интервалов), в которых содержится один и только один корень уравнения.

2. Уточнение приближенных корней, т.е. доведение их до заданной степени точности.

Билет 39. Отделение корней

• графический способ

• определение знаков функции в ряде промежуточных точек, выбор которых учитывает особенности функции

• специальные способы анализа функции

Билет 40 Метод простой итерации.

Дано уравнение

f(x) = 0

Заменим уравнение f(x)=0 равносильным уравнением

x = z(x)

Выберем каким-либо способом грубо приближенное значение x0

X1=z(x0), Xn=z(Xn-1)

Метод является одношаговым.

Билет 41 Условия сходимости метода простой итерации

Метод простой итерации сходится при условии, что производная функции z(x) по модулю меньше 1.(Рисовать графики расположения y=x и y=z(x))

Билет 42 Преобразование к виду x=z(x)

Билет № 43 Метод Ньютона и его модификации.

Предположим, что каким-либо методом (например, графическим) определено начальное приближение корня: x=x0

Обычно

Для окончания итерационного процесса может быть использовано условие

│f(xn) │ < ε или условие близости двух последовательных приближений

│xn+1 - xn│<ε .

Метод Ньютона обладает высокой скоростью сходимости.Обычная абсолютная точность решения 10-5-10-6 достигается через 5-6 итераций.

Недостатком метода является необходимость вычисления на каждой итерации не только функции f(x), но и её производной.

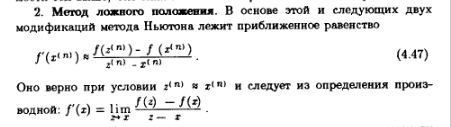
Билет№44. Метод Вегстейна.

Это совместное применение итерационной формулы:

, где и итерационной формулы простых итераций , где Начальные значения

Для оценки погрешности приближенного решения может использоваться неравенство , где это или подходящая оценка снизу этой величины.

Билет №45.Метод секущих

Билет №46. Метод параболической аппроксимации

Билет №47. Комбинированный метод.

Он состоит в одновременном использовании как метода касательных, так и метода хорд.

если для метода хорд последовательность значений, начиная от первоначального значения a - левого конца промежутка, возрастает, то для этого же случая по методу касательных последовательность убывает.

Для других двух случаев получается наоборот. Таким образом, получаемые последовательности сближаются и тем самым, применяя одновременно два метода можно получить более быстрое приближение корня.

Если мы имеем дело со случаем 1, тогда, обозначая приближенные значения по методу хорд x₁, а по методу касательных - z₁, получим:

 

тогда, a < x₁ < c < z₁ < b.

 

При следующем шаге заменяется в этих формулах a и b через x₁ и z₁:

  Общие формулу для построения приближений будут следующими:

 

  О качестве достигнутого приближения, т.е. о точности, можно судить по величине |z_n - x_n| - в этом удобство комбинированного метода.

Достоинства: 1) вдвое меньше выч. затрат 2) симм. матрицы А экономит память 3) гарант. устойчивость

Билет №48.Метод Мюллера

Идея метода секущих развивается в методе Мюллера. Однако в этом методе для нахождения очередного приближения используются три предыдущие точки. Иными словами, метод использует не линейную, а квадратичную интерполяцию функции. Расчетные формулы метода следующие:

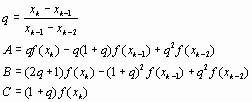
Знак перед корнем выбирается так,чтобы абсолютное значение знаменателя было максимальным.Поскольку поиск корня заканчивается, когда выполнится условие , то возможно появление ложных корней. Например, для уравнения ложный корень появится в том случае, если точность поиска задана меньше, чем 0,0001. Увеличивая точность поиска, можно избавиться от ложных корней. Однако не для всех уравнений такой подход работает. Например, для уравнения , которое, очевидно, не имеет действительных корней, для любой, сколь угодно малой точности найдется значение x, удовлетворяющее критерию окончания поиска. Приведенные примеры показывают, что к результатам компьютерных вычислений всегда нужно относиться критически, анализировать их на правдоподобность. Чтобы избежать "подводных камней" при использовании любого стандартного пакета, реализующего численные методы, нужно иметь хотя бы минимальное представление о том, какой именно численный метод реализован для решения той или иной задачи. В том случае, когда известен интервал, на котором расположен корень, можно воспользоваться иными методами нахождения решения уравнения.

Билет №49.Метод Гаусса-Жорданна

Билет № 50. Методы решения ОДУ.

Билет №52 Метод Эйлера

Численное решение задачи Коши методом Эйлера.

Численное решение задачи Коши состоит в построении таблицы приближенных значений в точках . Точки , называются узлами сетки, а величина - шагом сетки. В основе построения дискретной задачи Коши лежит тот или иной способ замены дифференциального уравнения его дискретным аналогом. Простейший метод основан на замене левой части уравнения правой разностной производной: . Разрешая уравнение относительно , получаем расчетную формулу метода Эйлера: , . Численный метод называется  явным, если вычисление решения в следующей точке осуществляется по явной формуле. Метод называется одношаговым, если вычисление решения в следующей точке производится с использованием только одного предыдущего значения . Метод Эйлера является явным одношаговым методом. Модификации метода Эйлера.Метод Эйлера обладает медленной сходимостью, поэтому чаще применяют методы более высокого порядка точности. Второй порядок точности по имеет усовершенствованный метод Эйлера : . Этот метод имеет простую геометрическую интерпретацию. Метод Эйлера называют методом  ломаных, так как интегральная кривая на отрезке заменяется ломаной с угловым коэффициентом . В усовершенствованном методе Эйлера интегральная кривая на отрезке заменяется ломаной с угловым коэффициентом, вычисленным в средней точке отрезка . Так как значение в этой точке неизвестно, для его нахождения используют метод Эйлера с шагом .

Билет №53.Метод Милна

Пусть на отрезке [a, b] требуется найти численное решение дифференциального уравнения с начальным условием . Разобьем отрезок [a, b] на n равных частей точками , где h=(b-a)/n – шаг интегрирования. Используя начальные данные, находим каким-либо способом последовательные значения искомой функции y(x). Таким образом, становитсяизвестным Приближения и для следующих значений последовательно находятся по формулам Милна

– где .

Абсолютная погрешность значения приближенно равна .

Пример. Дано дифференциальное уравнение y’=y-x, удовлетворяющие начальному условию x₀=0, y(x₀)=1,5. Вычислить с точность до 0,01 значение решения этого уравнения при x=1,5.

Решение. Выберем начальный шаг вычисления. Из условия h⁴<0,01 получим h=0,25 Составим таблицу

Получаем ответ y=(1,5)=4,74.

Билет №54. Метод Рунге-Кутты.

Изложим идею метода на примере: Интегрируя это уравнение в пределах от x до x + h (0 < h <1), получим равенство которое посредством последнего интеграла связывает значения решения рассматриваемого уравнения в двух точках, удаленных друг от друга на расстояние шага h. ∆y=y(x+h)–y(x) и замену переменной интегрирования t=x+h. Окончательно получим:

Указав эффективный метод приближенного вычисления интеграла выражении , мы получим при этом одно из правил численного интегрирования уравнения

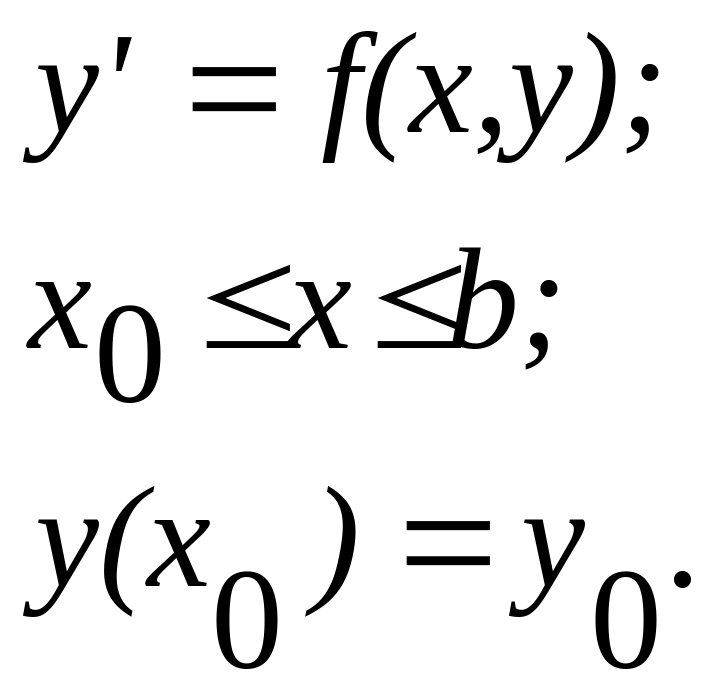
Постараемся составить линейную комбинацию величин _i, i = 0, 1, ..., q, которая будет являться аналогом квадратурной суммы и позволит вычислить приближенное значение приращения y: где

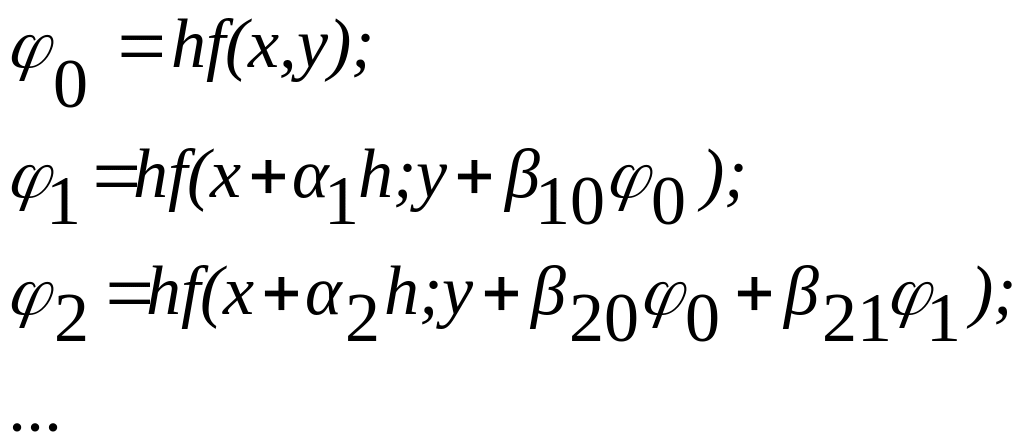Метод четвертого порядка для q = 3, имеет вид где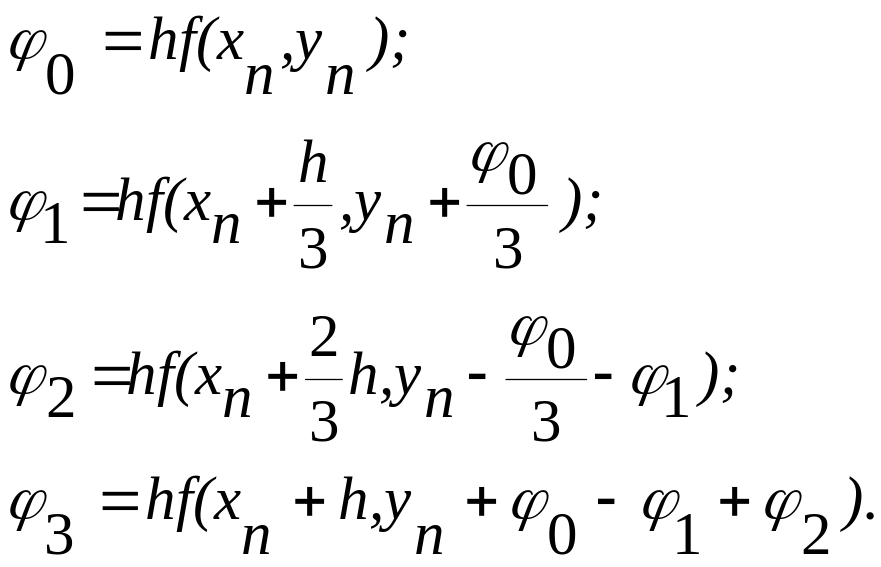

Особо широко известно другое вычислительное правило Рунге-Кутта четвертого порядка точности: где

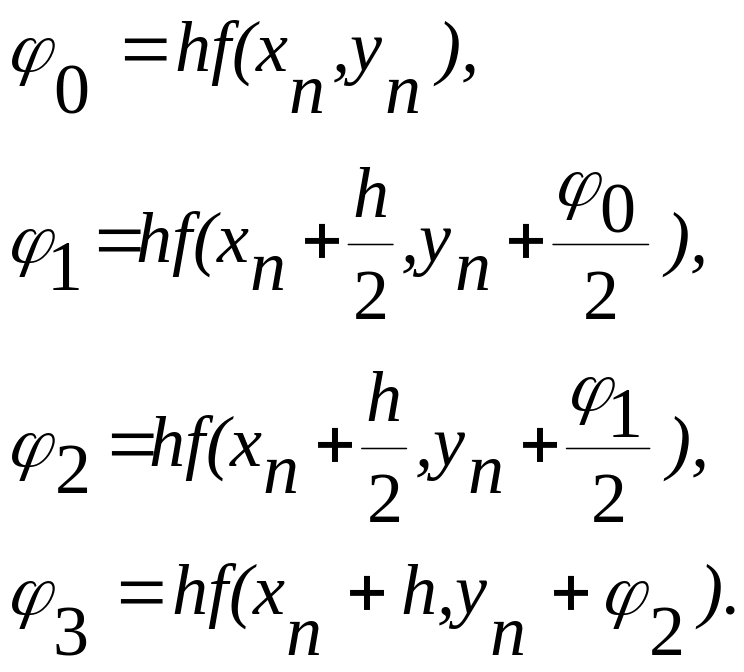
Метод Рунге-Кутта имеет погрешность четвертого порядка (~ h⁴ ).Правило Рунге. Если приближенный метод имеет порядок погрешности m, то погрешность можно приближенно оценить по формуле

В формуле O(x_i) – главный член погрешности, и - приближенные решения в точке x_i, найденные с шагом h и 2h соответственно.

Билет №55.Автоматический выбор шага

Билеты №56 Процедура Гилла

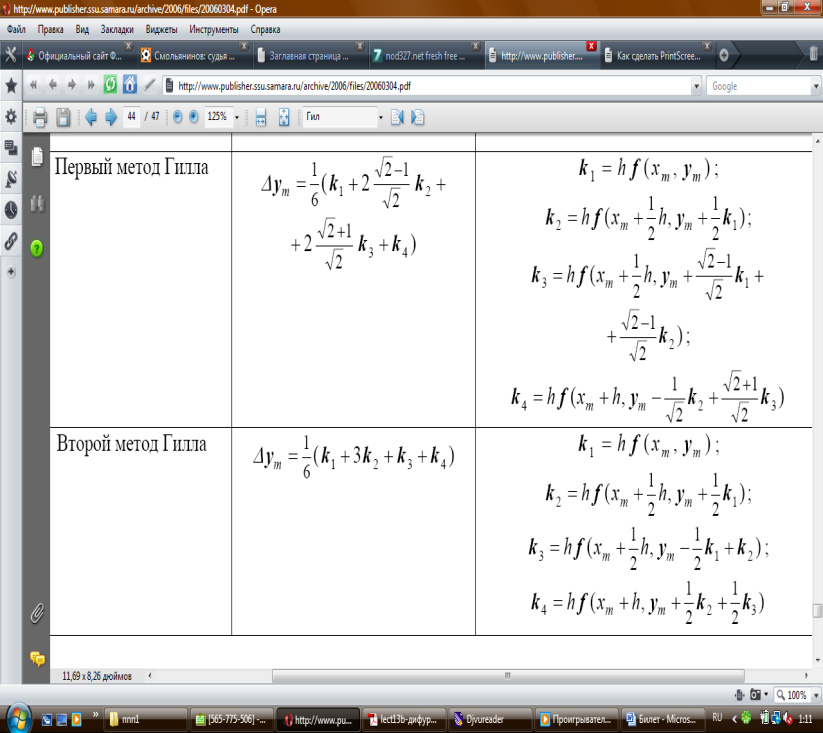
Билет №57