29. Поглощение и излучение света атомом водорода. Ионизация атома водорода.

Согласно второму постулату Бора возможные частоты излучения атома водорода определяются формулой _kn=(E_k-E_n)/h=(me⁴/(4h³))(1/n²-1/k²)=R(1/n²-1/k²), где R – постоянная величина, определяемая через постоянную Планка, массу и заряд электрона. Теория Бора приводит к количественному согласию с экспериментом для значений частот, излучаемых атомом водорода. Все частоты излучений атома водорода образуют ряд серий, каждой из которых соответствует определенное значение числа n и различные значения числа k>n. 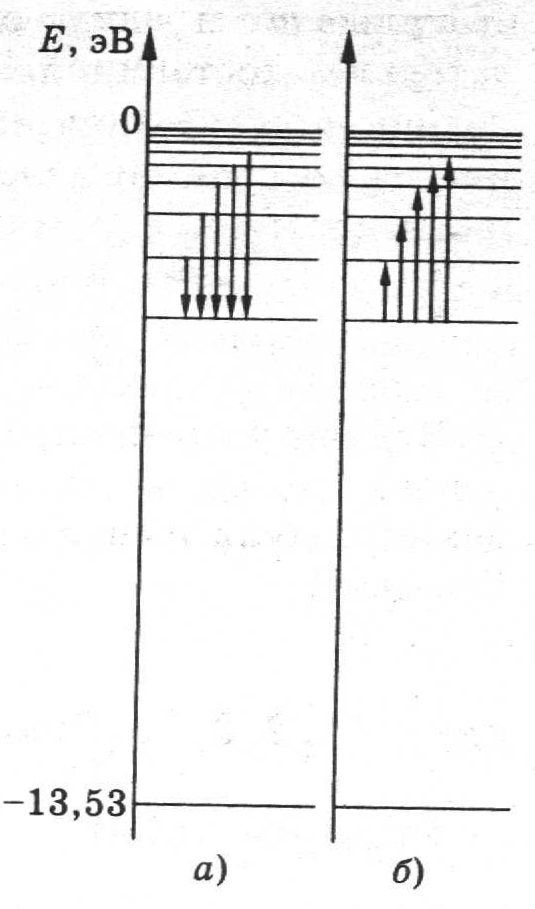Излучение частот данной серии происходит при переходах с высших энергетических уровней на один из низших. Переходы в первое возбужденное состояние (на второй энергетический уровень) с верхний уровней образуют серию Бальмера. На рисунке эти переходами изображены стрелками. Поглощение света – процесс, обратный излучению. Атом, поглощая свет, переходит из низших энергетических состояний в высшие. При этом он поглощает излучение той же самой частоты, которую излучает, переходя из высших энергетических состояний в низшие. На правой части рисунка стрелками изображены переходы атома из одних состояний в другие с поглощением света. Энергия ионизации – энергия, необходимая для удаления электрона из атома, находящегося в основном состоянии. Для атома водорода E_i=13,6 эВ. Энергия связи данного состояния – энергия, необходимая для удаления электрона из атома, находящегося в данном возбужденном состоянии. Например, энергия связи первого возбужденного состояния (n=2) равна 3,48 эВ. Энергия возбуждения – энергия, которую надо сообщить атому, чтобы электрон из основанного состояния перешел в возбужденное. Например, энергия связи первого возбужденного состояния перешел в возбужденное. Например, энергия для первого возбужденного состояния (n=2) E_возб=-3,48-(-13,6)10,1 эВ. Из энциклопедии: ионы (от греч. ion — идущий), электрически заряженные частицы, образующиеся из атома (молекулы) в результате потери или присоединения одного или нескольких электронов. Ионизация, превращение атомов и молекул в ионы. Степень ионизации — отношение числа ионов к числу нейтральных частиц в единице объема. Ионизация в электролитах происходит в процессе растворения при распаде молекул растворенного вещества на ионы (электролитическая диссоциация); в газах — в результате отрыва от атома или молекулы одного или нескольких электронов под влиянием внешних воздействий; в случае прилипания электрона к атому или молекуле может образоваться отрицательный ион. Энергия, необходимая для отрыва электрона, называется энергией ионизации. Ионизация происходит при поглощении электромагнитного излучения (фотоионизация), при нагревании газа (термическая ионизация), при воздействии электрического поля, при столкновении частиц с электронами и возбужденными частицами (ударная ионизация) и др.

30. Волновая функция микрочастицы и ее физический смысл. В общем случае (произвольное движение частицы в произвольных силовых полях) состояние частицы в квантовой механике задается волновой функцией (или пси-функцией) (r,t), зависящей от координат и времени. Она – основной носитель информации о корпускулярных и волновых свойствах микрочастиц. В частном случае свободного движения частицы волновая функция – плоская волна де Бройля. На основании статистической интерпретации волновой функции вероятность нахождения частицы в момент времени 0е с координатами x и x+dx, y и y+dy, z и z+dz определяется интенсивностью волновой функции, т.е. квадратом пси-функции. ²=. Поскольку в общем случае  - комплексная функция, а вероятность должна быть всегда действительной и положительной величиной, то за меру интенсивности принимается квадрат модуля волновой функции. Физический смысл пси-функции: вероятность dW нахождения частицы в элементе объема dV в момент времени t. dW=²dV. w=dW/dV=². Плотность вероятности, т.е. вероятность нахождения частицы в момент времени t в окрестности данной точки пространства. Плотность вероятности – величина, наблюдаемая на опыте, в то время как сама волновая функция, являясь комплексной, наблюдению недоступна. В этом заключается существенное отличие в описании состояний частиц в квантовой и классической механике (в классической механике величины, описывающие состояние частиц, наблюдаемы). Вероятность найти частицу в момент времени t в некотором объеме V W=_VdW=_V²dV.

Условие нормировки вероятностей _-^+(x,y,z,t)²dV=1. Так как ²dV определяется как вероятность, то, проинтегрировав это выражение в бесконечных пределах, получим вероятность того, что частица в момент времени t находится где-то пространстве. Это есть вероятность достоверного события, а ее в теории вероятностей считают равной 1. Волновая функция – объективная характеристика состояния микрочастиц и должна удовлетворять ряду ограничений. Она должна быть конечной (вероятность не может быть больше единицы), однозначной (вероятность не может быть неоднозначной величиной) и непрерывной (вероятность не может изменяться скачком). Также см. лекции.

31. Принцип суперпозиции для волновых функций. Операторы физических величин. Соотношение неопределенностей. Также см. лекции. Принцип суперпозиции для волновых функций: =_nC_n_n. Если какая-либо система (частица или их совокупность) может находиться в различных состояниях, описываемых волновыми функциями ₁, ₂, …, _n, …, то она может находиться в состоянии , описываемом линейной комбинацией этих функций. В указанной формуле C_n, n=1, 2, … - произвольные (в общем случае комплексные) числа, при этом квадрат модуля коэффициента C_n, т.е. C_n², равен вероятности обнаружить, что система, представленная состоянием , может оказаться в состоянии _n. Сложение волновых функций (амплитуд вероятностей), а не вероятностей (определяемых квадратами модулей волновых функций) принципиально отличает квантовую теорию от классической статистической теории, в которой для независимых событий справедлива теорема сложения вероятностей. В классической механике описание поведения материальной точки или других тел производится с помощью задания динамических переменных, т.е. значений координат, импульсов, энергии и т.д. Строго говоря, микрочастицам не могут быть приписаны вполне точные значения динамических переменных. Но поскольку информация о движении микрочастиц получается с помощью измерительных приборов, т.е. микроскопических тел, то поневоле описание микрочастиц производится с помощью динамических переменных. Поэтому мы говорим иногда, что электрон, например, обладает определенным импульсом, энергией и т.д. Но при этом оказывается, что не любые динамические переменные могут иметь определенные значения. Согласно принципу неопределенности, микрочастица не может одновременно иметь вполне точные значения координаты и соответствующего ей импульса P_x. Неопределенности этих величин x и P_x связаны соотношением xP_xh. Из этого соотношения следует, что чем точнее измерена одна из величин, тем более неопределенной становится другая. Так, если одна из этих величин изменяется вполне точно, другая становится совершенно неопределенной. Аналогичные соотношения yP_yh, zP_zh.Также E_qt_qh. Математический аппарат квантовой механики. Согласно соотношению неопределенностей, в квантовой области не существует таких состояний, в которых координата частицы и соответствующая ей проекция импульса имели бы одновременно точные значения. Это находит свое отражение и в формальной стороне теории – математический аппарат квантовой механики резко отличается от математического аппарата классической механики. Кроме того, он должен соответствовать физической постановке задач квантовой механики, например, учитывать волновые свойства микрочастиц. В квантовой механике используют представление физических величин с помощью математических операторов. Свойства операторов. f(x)=L^{^}(x). Правило, с помощью которого какой-то функции (x) некоторой переменной сопоставляется функция f(x) той же переменной. Символически это записывается в виде умножения L^{^} (операторы обозначаются буквами со «шляпкой» над ними) на (x). Сложение, вычитание и умножение операторов производится по обычным алгебраическим правилам сложения, вычитания и умножения чисел. Сумма операторов С^{^}=A^{^}+B^{^}. Разность операторов D^{^}=A^{^}-B^{^}. При умножении операторов не всегда A^{^}B^{^}=B^{^}A^{^}. Произведение операторов F^{^}=A^{^}(B^{^}). A^{^}B^{^}=B^{^}A^{^}- коммутирующие операторы. A^{^}B^{^}B^{^}A^{^} - некоммутирующие операторы. Линейный оператор L^{^}(С₁₁+С₂₂)=С₁L^{^}₁+C₂L^{^}₂. Оператор линейный, если для любых двух функций ₁ и ₂ и любых постоянных С₁ и С₂ выполняется записанное условие. В квантовой механике применяются только линейные операторы (чтобы применение операторов не нарушало принципа суперпозиции состояний). Линейный Эрмитов оператор ₁*L^{^}₂dV=₂L^{^}*₁*dV. Оператор эрмитов, если выполняется записанное условие: ₁ и ₂ – произвольные функции (звездочка означает операцию комплексного сопряжения), а интегрирование производится по всей области изменения независимых переменных. Подробнее об операторах – в лекциях.

32. Уравнение Шредингера. Нестационарные и стационарные состояния. Стационарные состояния свободной частицы. Также см. лекции. Статистическое толкование волн де Бройля и соотношение неопределенностей Гейзенберга привели к выводу, что уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть уравнение, из которого бы вытекали наблюдаемые на опыте волновые свойства частиц. Основное уравнение должно быть уравнением относительно волновой функции (x,y,z,t), так как именно она, или, точнее, величина ², определяет вероятность пребывания частицы в момент времени t в объеме dV, т.е. в области с координатами x и x+dx, y и y+dy, z и z+dz. Так как искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравнению, описывающему электромагнитные волны. Основным уравнением квантовой механики является уравнение Шредингера. Подобно тому, как основные законы физики (например, законы динамики Ньютона, уравнения Максвелла для электромагнитного поля) не выводятся теоретически, а являются обобщением огромного числа опытных фактов, уравнение Шредингера тоже не может быть выведено из каких-либо известных ранее соотношений. Оно постулируется. Уравнение Шредингера следует рассматривать, как исходное предположение, доказательство которого объясняется тем, что следствия, вытекающие из уравнения Шредингера самым точным образом подтверждаются наукой. Временное уравнение Шредингера –(h²/[2m])+U(x,y,z,t)=ih(/t), где h=h/2, m – масса частицы,  - оператор Лапласа (=²/x²+²/y²+²/z²), i – мнимая единица. Условия, накладываемые на волновую функцию: 1) волновая функция должна быть конечной, однозначной и непрерывной; 2) производные /x, /y, /z, /t должны быть непрерывны; 3) функция ² должна быть интегрируема (это условие сводится к условию нормировки вероятностей); 4) уравнение Шредингера справедливо для нерелятивистских частиц (скорости v<<c). Стационарные состояния – состояния с фиксированными значениями энергии. Представление волновой функции для стационарных состояний (x,y,z,t)=(x,y,z)e^-(i/h)Et. В случае стационарного силового поля (функция U=U(x,y,z) не зависит от времени и имеет смысл потенциальной энергии) волновая функция представляется в виде произведения двух функций: одна – функция только координат, другая функция – только времени (зависимость от времени выражается множителем e^-it=e^-(i/h)Et. Стационарное уравнение Шредингера +(2m/h²)(E-U)=0 (получается после подстановки волновой функции во временное уравнение Шредингера и преобразований). В выше указанном уравнении  - координатная (амплитудная) часть волновой функции (x,y,z,t) стационарного состояния ( также называют волновой функцией); Е – полная энергия частицы, U=U(x,y,z) – ее потенциальная энергия,  - оператор Лапласа. В уравнение Шредингера в качестве параметра входит полная энергия Е. Реальный физический смысл имеют только те решения, которые выражаются регулярными функциями  ( должны быть конечными, однозначными и непрерывными вместе со своими первыми производными). Регулярные решения имеют место лишь при определенном наборе E, отвечающем данной задаче. Эти значения энергии называют собственными. Они могут образовывать как непрерывный, так и дискретный спектр энергий. Далее - см. лекции.