Лекция 1.

Основные понятия.

Изучаются общие методы структурного, кинематического, и динамического анализа и синтеза механизмов и машин.

Механизм – это устройство, выполняющее преобразование движения одного или нескольких твердых тел в требуемое движение других твердых тел.

Машина – это устройство, выполняющее механические движения для преобразования энергии, материалов или информации.

Различают группы машин:

1) Энергетические (ДВС).

2) Технологические (станки, прессы).

3) Информационные (преобразование и переработка информации).

Звенья и кинематические пары.

Звено – это одно или несколько жестко соединенных твердых тел, входящих в состав механизма.

В каждом механизме имеется стойка (звено неподвижное или принимаемое за неподвижное).

Входные и выходные звенья.

Входное звено – это звено, которому сообщается движение, преобразуемое механизмом в требуемое движение других звеньев.

Выходное звено – это звено, совершающее движение, для выполнения которого предназначен механизм.

Кинематическая пара – это подвижное соединение двух соприкасающихся звеньев.

По числу степеней свободы в соединениях звеньев различают 1,2,3,4 и 5 – подвижные кинематические пары.

Вращательная КП.

Поступательная КП.

Винтовая КП.

Цилиндрическая КП.

Сферическая КП.

Сферическая КП с пальцем двухподвижная.

Плоскостная КП с пальцем трехподвижная.

Линейчатая КП четырехподвижная.

(Цилиндр на плоскости).

Точечная КП пятиподвижная.

(Шар на плоскости)

Иногда различают кинематические пары по классам. Номер класса определяется числом наложенных связей, т.е. он равен: 6- (число подвижностей).

По характеру соприкосновения звеньев различают низшие и высшие кинематические пары.

Низшие пары могут быть выполнены соприкосновением звеньев по поверхностям или по плоскостям.

Высшие – соприкосновением по линиям или в точках.

Кинематические цепи.

Определение: кинематическая цепь – это система звеньев, связанных между собой кинематическими парами.

Кинематические цепи могут быть:

1) Замкнутыми и незамкнутыми.

2) Плоскими и пространственными.

Число степеней свободы механизмов.

Определение: числом степеней свободы механизма называется число независимых между собой параметров, однозначно определяющих положение всех звеньев относительно стойки. Эти независимые параметры называются обобщенными координатами механизма. Так как свободное тело в пространстве имеет “6” степеней свободы, то, будучи свободными, “n” подвижных звеньев механизма имели бы “6n” степеней свободы. Так как каждая пара “i-й” подвижности накладывает на относительное движение “6-i” связей, то общее число таких связей равно сумме:

p_i - число “i-й” подвижности.

Число степеней свободы пространственного механизма:

Для плоских механизмов:

Пример 1(плоский кривошипно–ползунный механизм).

Число подвижных звеньев: n=3.

Число низших КП: p_H = 4.

- вращательные.

- поступательные.

За обобщенную координату можно принять .

Начальное звено – это звено, которому приписывается обобщенная координата.

Пример 2 (пространственный механизм)

Число подвижных звеньев: n=3.

Число низших КП: p₁ = 1.

[A(1,0)].

Число высших КП: p₂ = 3.

Начальное звено – стойка “1”.

Пример 3 (пространственный механизм манипулятора).

Число подвижных звеньев: n=3.

p₁ = 1. - [B(1,2)].

p₃ = 2. – [A(1,0),C(2,3)].

Нужно задать три угла поворота А и С

и один угол поворота В.

Пассивные связи и местные (лишние) степени свободы.

В некоторых механизмах имеются пассивные (избыточные) связи, которые дублируют ограничения, наложенные другими связями. В результате расчетное значение “W” получается меньше фактического.

Лекция 2.

Пример 1(механизм двойного шарнирного параллелограмма).

;

В действительности W = 1. Пассивную связь вносит звено “4”, так как и без него звено “3” будет вращаться со скоростью, равной ω₀. Если условно удалить звено “4”, то получим:

.

Однако звено “4” позволяет устранить неопределенность в движении, когда все звенья выстраиваются в одну линию.

Пример 2 (комбинированный зубчатый механизм)

Число подвижных звеньев: n=3.

Число низших КП: p₁ = 1.

[A(1,0),CC’(2,0),E(3,0)].

Число высших КП: p₂ = 3.

[B(1,2), D(2’,3)].

Местные (лишние) степени свободы обычно вносят в круглые ролики.

Пример 3 (кулачковый механизм)

Число подвижных звеньев: n=3.

Число низших КП: p₁ = 3.

[A(1,0),C(2,3),В(3,0)].

Число высших КП: p₂ = 1.

[B(1,2)].

Вращение круглого ролика “2” представляет собой местную степень свободы. Она не влияет на движение выходного звена “3”, поэтому достаточно задать движение кулачку “1”.

Принцип Ассура.

Указанный принцип, предложенный в 1914 году русским ученым Асуром, состоит в том, что механизм образуется из начального механизма и одной или нескольких структурных групп.

Начальный механизм состоит из стойки и одного или нескольких начальных звеньев и имеет такое же число степеней свободы, как и весь механизм (механизм первого класса).

Структурной группой или группой Ассура называется такая кинематическая цепь, которая после присоединения ее внешними кинематическими парами к стойке имеет нулевую подвижность и которая не распадается на более простые цепи, удовлетворяющие этому условию. Согласно определению , этому условию удовлетворяют соотношения:

n	2	4	6
pH	3	6	9

Простейшей является структурная группа, у которой число подвижных звеньев: n=2 и

число низших КП: p_H = 3. Она называется структурной группой 2-го класса, 2-го порядка и существует в пяти видах:

Порядок структурной группы определяется числом ее внешних кинематических пар.

Группы, у которых n=4 и p_H=6, могут быть 3 и 4 класса.

Класс структурной группы определяется числом внутренних кинематических пар, образующих наиболее сложный замкнутый контур.

Пример 4.

Число подвижных звеньев: n=5.

Число низших КП: p₁ = 7.

[A(1,0),B(1,2),C(2,3),C(3,4),D(3,0),E(4,5),E(5,0)].

Начальное звено – 1.

Согласно Ассуру, берется начальное звено и стойка.

Формула строения механизма:

Класс механизма определяется высшим классом группы, входящей в ее состав.

Рассмотрим механизм – механизм второго класса.

Структурный анализ механизма позволяет установить последовательность и методы его кинематического и силового анализа.

Существуют механизмы, образование которых не подчиняется принципу Ассура. Это механизмы с заданным относительным движением звеньев.

Пример.

S – обобщенная координата.

Число подвижных звеньев: n=3.

Число низших КП: p₁ = 4.

[A(1,0),В(2,3),С(3,0),D(1,2)].

Здесь нельзя указать, какое звено является

Начальным. Можно указать начальную

кинематическую пару. Это пара D.

Задачи кинематического анализа механизмов.

Кинематический анализ механизмов состоит в определении движения его звеньев по заданному движению начальных звеньев.

Основные задачи:

1. Определение положений звеньев и траекторий отдельных точек.

2. Определение линейных скоростей и ускорений точек и угловых скоростей и ускорений звеньев.

3. Определение передаточных функций или отношений между звеньями.

Методы кинематического анализа:

1) Графические.

2) Аналитические.

Масштабный коэффициент показывает, сколько единиц той или иной величины приходится на 1 мм отрезка, изображающего эту величину.

- масштабный коэффициент.

Кинематический анализ плоских рычажных механизмов графическим методом.

Пример 1 (кривошипно – ползунный механизм).

Известны размеры звеньев, положение

механизма, закон движения начального

звена ( ).

;

;

в сторону

находим отрезок РА:

На основании теоремы о сложении скоростей в плоскопараллельном движении:

, где - относительная скорость точки В при вращении звена “2” вокруг точки “A”.

параллельна оси “X”. Это уравнение решаем графически путем построения плана скоростей.

;

.

Направление указывает вектор , если перенести его точку “B” и рассмотреть движение звена “2” вокруг точки “A”.

Решаем графически:

Свойства планов скоростей.

1. Отрезки, выходящие из полюса, выражают абсолютные скорости точки.

2. Отрезки, соединяющие концы векторов абсолютных скоростей, изображают относительные скорости .

3. Теорема подобия: концы векторов абсолютных скоростей точек, принадлежащих одному звену, образуют фигуру, подобную соответствующей фигуре звена и сходственно с нею расположенную.

и - подобны.

Сходственное расположение обозначает, что направление обхода одноименных контуров совпадают.

- по часовой стрелке.

Ускорение

- от т.”A” к “O”

в сторону

- масштабный коэффициент.

;

Построение:

Ускорение точки “B”:

от “В” к “А”.

; параллельно “Х”.

Решаем графически:

Направление указывает вектор , если перенести его в точку “B” и рассмотреть движение точки “B” относительно “A”.

Точку “k” находим по свойству подобия, которое справедливо и для плана ускорений. Для этого методом засечек строим треугольник и сходственно с ним расположенный:

Пример 2 (четырехшарнирный механизм ).

- масштабный коэффициент

План скоростей.

План ускорений.

в сторону

- коэффициент скоростей

- отрезок в миллиметрах

По теореме сложения скоростей:

Угловые ускорения:

Точку “K” определяем по теореме подобия:

Определение ускорений:

- масштабный коэффициент ускорений

Точку “K” находим по теореме подобия:

Пример 3 (кулисный механизм).

Заданными являются относительное движение поршня “2” по отношению к цилиндру “1” (скорость ν_n и ускорение поршня a_n ).

Далее будем рассматривать кинематически эквивалентную схему.

Различаем точки “A” и “A₂”. А – неподвижная точка – центр вращательной пары;

А₂ – точка, принадлежащая звену “2” и в данный момент совпадающая с точкой “A”.

Рассматриваем движение звена “2” как сложное, которое складывается из переносного (вращательного) движения вместе со звеном “1” и относительного (поступательного) по отношению к звену “1”:

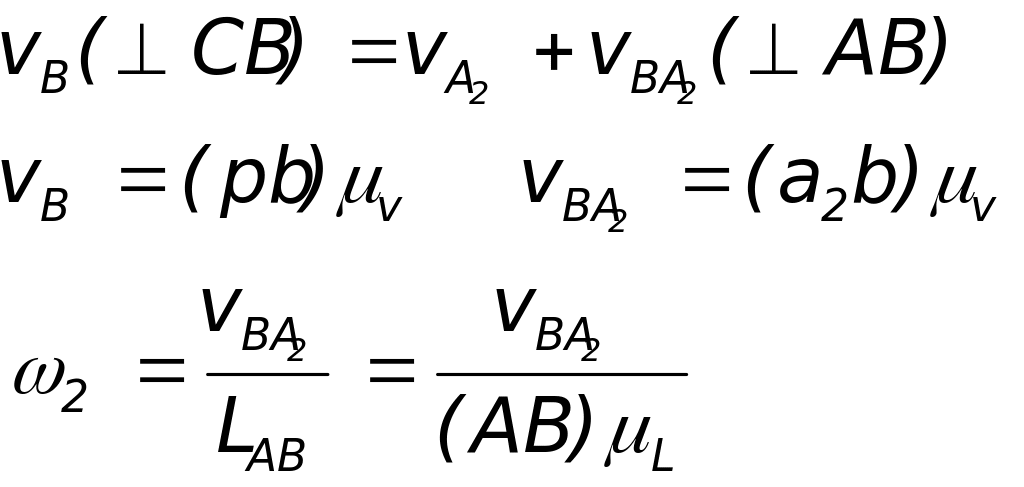
- общее переносное движение

- вращение “B” вокруг “C”

Находим ускорения:

Ускорение точки “A₂”:

- заданное относительное ускорение

В общем случае:

Для плоских механизмов угол между ω_пер и ν_отн равен 90⁰. Тогда:

Направление указывает вектор относительной скорости , повернутый на 90⁰ в сторону ω₂.

Отрезок, изображающий а_П, равен:

Лекция 3.

Функция положения. Аналоги скоростей и ускорений.

Функция положения – это зависимость координаты звена от обобщенной координаты механизма .

- функция положения звена “n”.

Аналог скорости – первая производная функции положения по обобщенной координате.

- аналог угловой скорости звена “n”.

- аналог скорости точки “N”.

Аналог ускорения – вторая производная функции положения по обобщенной координате.

- аналог угловой скорости звена “K”.

- аналог ускорения точки “N”.

Из этих формул видно, что если , то аналоги скоростей и ускорений равны соответствующим скоростями ускорениям.

Аналоги скоростей и ускорений не зависят от времени и закона движения начального звена.

Аналоги скоростей называются передаточными функциями.

;

Используются и другие обозначения.

Передаточные функции можно найти с помощью планов скоростей. Например:

Определение кинематических характеристик плоских рычажных механизмов аналитическим методом.

Пример 1 (кривошипно – ползунный механизм).

Известно:

- эксцентриситет

(смещение);

- обобщенная координата.

Решение.

Используем метод замкнутых векторных контуров.

Контур ОА ВО:

Проецируем это уравнение на оси координат:

(1)

(2)

Из (2) находим :

Знак “+”, если ползун “3” находится справа от центра “O”.

Знак “-”, если ползун “3” находится слева от центра “O”.

После нахождения определяем из (1):

Дифференцируем уравнения (1) и (2) по обобщенной координате . При этом:

(3)

Проекция на ось “Y”:

(4)

Из (4) находим аналог угловой скорости звена “2”:

Дифференцируем (3) и (4) по :

(5)

(6)

Из (6) находим аналог углового ускорения звена “2”:

Из (5):

Для точки “3” можно записать:

Зная , можно найти все скорости и ускорения:

Получим приближенные формулы, когда :

При можно ограничиться первыми двумя членами ряда:

ОТВЕТ.

Пример 2.

Имеем замкнутый контур OABC:

Составляем уравнение его контурности:

(1)

(2)

, где “+” – если обход контура АВС будет против часовой стрелки,

где “-” – если обход контура АВС будет по часовой стрелке.

“β” находим из ∆ АВС по тереме косинусов:

После определения определяются , и угол из (1) и (2).

Дифференцируем (1) по :

(3)

Из всех углов в уравнении (3) вычитаем угол , что равносильно повороту осей координат на этот угол. Получаем аналог угловой скорости звена “2”:

Далее вычитаем :

Дифференцируем (3) по :

(4)

Пример 3 (кулисный механизм).

- обобщенная

координата.

Используем метод замкнутых векторов.

Берем контур АВСА:

Проецируем это уравнение на оси координат:

(1)

(2)

, где “+” – если по часовой стрелке, а “-” – против часовой стрелки.

По теореме косинусов:

∆ АВС:

Дифференцируем (1) по “S”:

- аналог угловой скорости звена “1”.

(3)

Вычитаем угол :

Вычитаем угол :

Дифференцируем (3) по “S”:

(4)

Вычитаем из угла . Тогда аналог:

Вычитаем :

Кинематика винтового механизма.

“Р” – шаг резьбы.

- ход винта

“Z” – число заходов

Чаще всего используется трапецеидальная резьба.

При повороте винта на один оборот (2π радиан) он переместится вдоль оси на величину h относительно неподвижной гайки. При повороте на угол переместится на расстояние S.

Скорость поступательного перемещения винта:

- параметр винта (отношение линейной скорости к угловой).

Различают винты с правой и левой винтовой линиями.

Во многих металлообрабатывающих применяется механизм, в котором ходовой винт “1” поступательно перемещает невращающуюся гайку “2”

1 – 0 – вращающаяся пара.

1 – 2 – винтовая пара.

2 – 0 – поступательная пара.

Для винтовой пары можем записать:

откуда передаточная функция:

Вывод: в случае правого винта (h>0) ν₁ и ω₁ имеют противоположное направление.

Виды зубчатых передач.

Передаточное отношение и передаточное число.

В зависимости от расположения осей вращения колес различают следующие виды зубчатых передач:

1) с параллельными осями (цилиндрические)

2) с пересекающимися осями (конические)

3) со скрещивающимися осями

Внешнее зацепление.

Внутреннее зацепление

- радиусы начальных окружностей

W – полюс зацепления

Начальные окружности – воображаемые окружности, которые перекатываются одна по другой без скольжения и радиусы которых обратно пропорциональны угловым скоростям:

- без скольжения

Передаточные отношения:

- числа зубьев колес

Знак “+” – внутреннее зацепление (ω₁ и ω₂ - сонаправлены )

Знак “-” – внешнее зацепление

Передаточное число – отношение числа зубьев большего колеса “2” к числу зубьев меньшего колеса “1”:

Цилиндрические колеса могут быть :

1) с прямыми зубьями

2) с косыми (винтовыми) зубьями

3) с шевронными зубьями

Частным случаем является реечная передача (цилиндрическая):

Коническая передача:

Чаше всего

- передаточное отношение

1) Винтовая зубчатая передача:

2) Червячная передача с цилиндрическим червяком:

1 – червяк

2 – червячное колесо

3) Червячная передача с глобоидным червяком

4) Гипоидная передача.

Z₁ – число заходов или витков в случае червячной передачи

Ступенчатые зубчатые передачи с неподвижными осями вращения.

Трехступенчатая передача:

1 – 2 – циклическая передача

2’ – 3 – коническая передача

- общее передаточное отношение

Перемножим передаточные отношения:

Таким образом:

Если все колеса – цилиндрические, то:

“k” – число внешних зацеплений.

Частным случаем является передача с промежуточными колесами:

2 – промежуточное колесо

- число зубьев промежуточного колеса не влияет на передаточное отношение.

Зубчатые механизмы с подвижными осями вращения.

Сюда относятся механизмы, в составе которых имеется хотя бы одно колесо с перемещающейся в пространстве осью вращения – сателлит.

Различают:

1) Дифференциальные механизмы.

2) Планетарные механизмы.

3) Замкнутые механизмы.

1 и 3 – центральные колеса

Н – водило

2 – сателлит

W – число степеней свободы

Механизм имеет два входа и один выход (или один вход и два выхода)

Получим формулу, связывающую угловые скорости звеньев в дифференциальном механизме.

Метод обращения движения: мысленно сообщаем всем колесам и водилу угловую скорость дополнительную. Тогда скорость в обращенном движении:

Формула Виллиса:

- передаточное отношение обращенного механизма

В общем виде:

Если в дифференциальном механизме одно из колес сделать неподвижным, то получится планетарный механизм.

3 – неподвижное колесо

Так как ω₃ = 0, то

- передаточное отношение планетарного механизма.

, где “b” – неподвижное колесо, “а” – номер любого колеса планетарного механизма.

Пример 1.

Задано:

n₁, число зубьев

Определить:

Решение.

2 ступени:

а) 1 – 2 – передача с неподвижными осями.

б) 2’ – 3 – 4 – Н – планетарная ступень.

Общее передаточное отношение:

По формуле Виллиса:

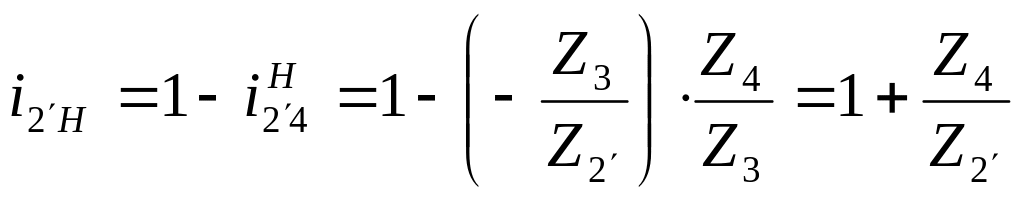
Так как то

Формула Виллиса для “3” и “4”:

Пример 2.

Задано:

n₁ – частота вращения,

числа зубьев.

Определить:

n₅.

Решение.

1) 1 – 2 – передача с неподвижными осями.

2) Н – 3 – 4 – 4’ – 5 – планетарная ступень.

Пример 3 (замкнутый дифференциальный механизм).

Решение.

1 – 2 – 2’ – 3 – Н – дифференциальная часть.

3’ – 4 – 5 – замкнутая цепь.

Для дифференциальной части формула Виллиса:

Для замыкающей цепи:

Тогда:

Делим почленно числитель и знаменатель на ω_Н. Тогда:

Волновая зубчатая передача.

1 – гибкое колесо

2 – жесткое колесо

Н – генератор волн с роликами (водило)

Вид справа.

При вращении генератора образуется бегущая по окружности волна деформации гибкого колеса. Так как , то это приводит к вращению гибкого колеса в противоположном направлении.

должно быть равной или кратной числу волн n_b. Обычно (как на рисунке).

В кинематическом отношении волновые передачи аналогичны планетарным:

Формула Виллиса:

В волновых передачах осуществляется многопарное зацепление зубьев, поэтому нагрузка на зубья значительно снижается, повышается плавность и мягкость работы. Для одноступенчатых передач:

Силы, действующие в машинах.

В машинах действуют следующие основные группы сил:

1) Движущие силы – совершают положительную работу и приложены к ведущим звеньям.

2) Силы технологического (полезного) сопротивления – совершают отрицательную работу и приложены к ведомым звеньям.

3) Силы тяжести и упругости звеньев – совершают как положительную, так и отрицательную работу. За кинематический цикл их работа равна нулю.

4) Силы взаимодействия между звеньями – реакции в кинематических парах – их нормальные составляющие работы не производят (реакции идеальных связей), касательные составляющие являются силами трения и обычно относятся к вредным сопротивлениям.

5) Расчетные силы – силы инерции – для учета неравномерности.

Динамическая модель машины с одной степенью свободы.

Что бы упростить решение задач динамики, машина заменяется динамической моделью в виде вращающегося звена приведения, к которому приложен приведенный момент сил М_П, и которое имеет приведенный момент инерции J_П (относительно оси вращения).

М_П и J_П должны определяться так, чтобы в любой момент:

, где - кинематические характеристики начального звена исполнительного механизма.

Если начальное звено совершает поступательное движение, то динамическая модель представляет собой точку приведения, к которой приложена приведенная сила F_П и которая имеет приведенную массу m_П.

Def: приведенным моментом сил “М_П” называется условный момент, который должен быть приложен к звену приведения, чтобы мощность этого момента равнялась сумме мощностей сил и моментов, действующих на звенья машины.

Согласно определению:

Если M_П>0, то это движущий момент; направлен в сторону

Если M_П< 0, то это момент сопротивления; направлен противоположно

или:

где:

- приведенный момент движущих сил

- приведенный момент сил сопротивления

Аналогично определяется - приведенная сила:

Def: приведенным моментом инерции машины “J_П” называется условный момент инерции, которым должно обладать звено приведения относительно оси его вращения, что бы кинетическая энергия этого звена равнялась сумме кинетических энергий всех звеньев машины:

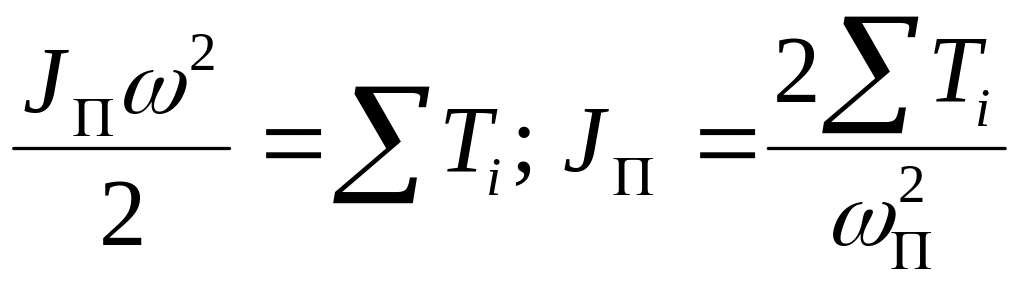
1) Поступательное движение:

- кинетическая энергия

2) Вращательное движение.

, где - момент инерции относительно оси вращения

3) Плоскопараллельное движение:

- центр масс

- центральный момент инерции.

Аналогично определяется приведенная масса m_П:

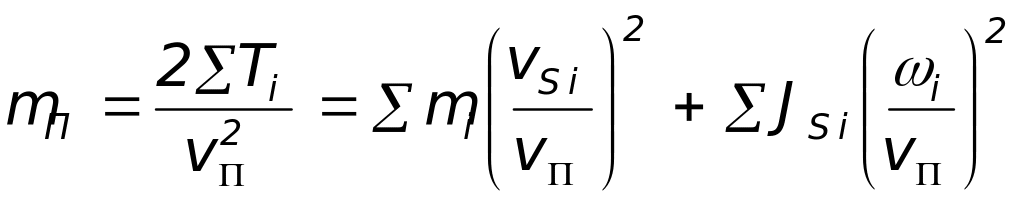
Пример 1.

Составить выражение для определения M_П и J_П:

Решение.

- внешние момент и сила.

- силы тяжести звеньев в центрах масс.

- вправо

- влево

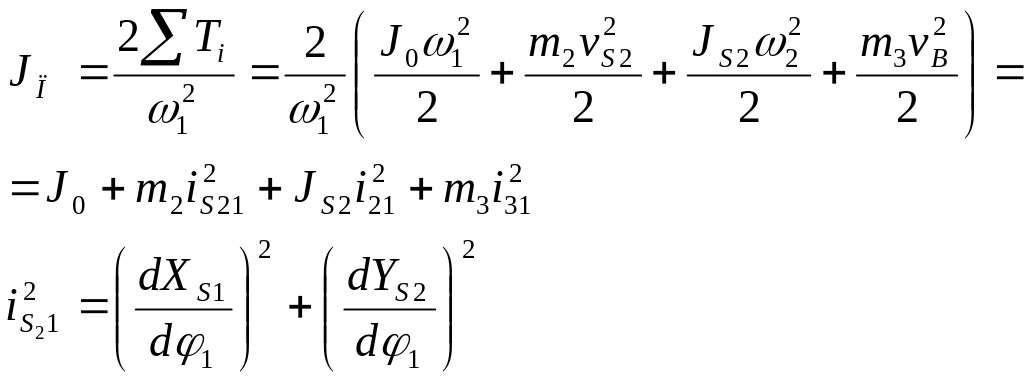
Пример 2.

М₁ – движущий момент

М_Н – момент сопротивления

М_П, J_П - ?

Решение.

По формуле Виллиса:

Пример 3.

- движущая сила

- сила тяжести

- относительная скорость поршня “2”

- обобщенная координата

Определить:

Приведенная сила - ?

Приведенная масса - ?

Решение.

Уравнение движения звена приведения.

Согласно теореме об изменении кинетической энергии:

(1)

- кинетическая энергия машины в начальном и конечном положениях.

- сумма работ всех сил на рассматриваемом перемещении.

, где:

- работа движущих сил

- работа сил сопротивления

Используя приведение сил и масс, уравнение (1) можно записать следующим образом:

- кинетическая энергия звена приведения

(2) – уравнение движения звена приведения в энергетической форме.

Согласно теореме об изменении кинетической энергии в дифференциальной форме:

Окончательно имеем

(3) – уравнение движения приведенного звена в дифференциальной форме.

(2’)

(3’)

Режимы движения машин.

В общем случае движения машины наблюдаются в следующих стадиях:

1) Разбег (разгон)

2) Установившееся движение

3) Выбег

1) Так как , то получаем:

, ω – возрастает.

2) ω – периодическая функция времени (в частном случае - касательная):

- за цикл.

или

- коэффициент неравномерности движения

3) ω – убывает.

Для уменьшения времени выбега используются тормозные устройства.

Определение закона движения звена приведения из дифференциального уравнения движения.

Пример.

1 – электродвигатель постоянного тока (с параллельным возбуждением).

2 – исполнительный механизм.

3 – редуктор.

М_g – движущий момент.

М_С – момент сопротивления.

- при разгоне.

Решение.

- прямая линия

- передаточное отношение редуктора

- касательная времени машины

- асимптотически приближается к установившемуся значению

При

Этот же результат можно получить из условия :

Теоретически процесс разгона продолжается бесконечно долго.

Полагая, что , находят реальное время разгона.

Пример 2.

Определить зависимость при выбеге центробежного насоса.

Решение.

- двигатель выключен.

При

Определение закона движения звена приведения из уравнения движения в энергетической форме.

Звено приведения:

Разгон:

- прямая линия

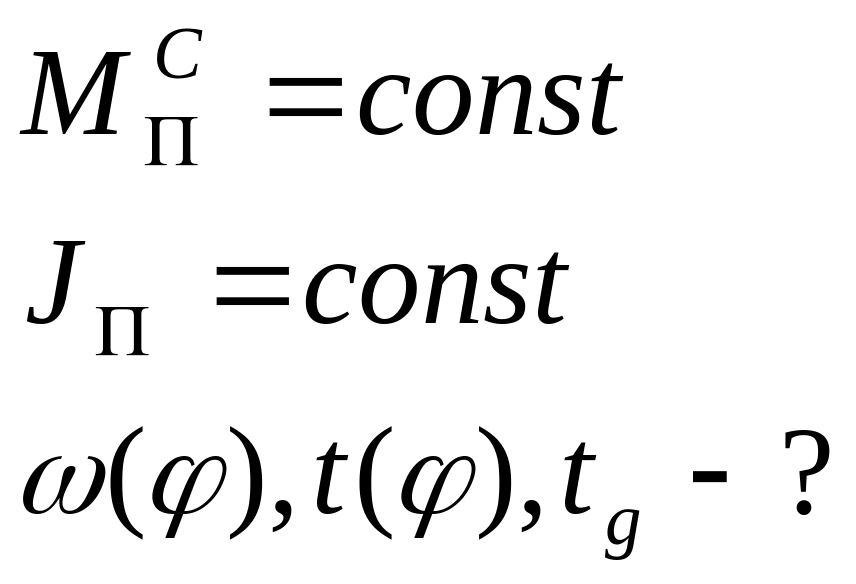
Решение.

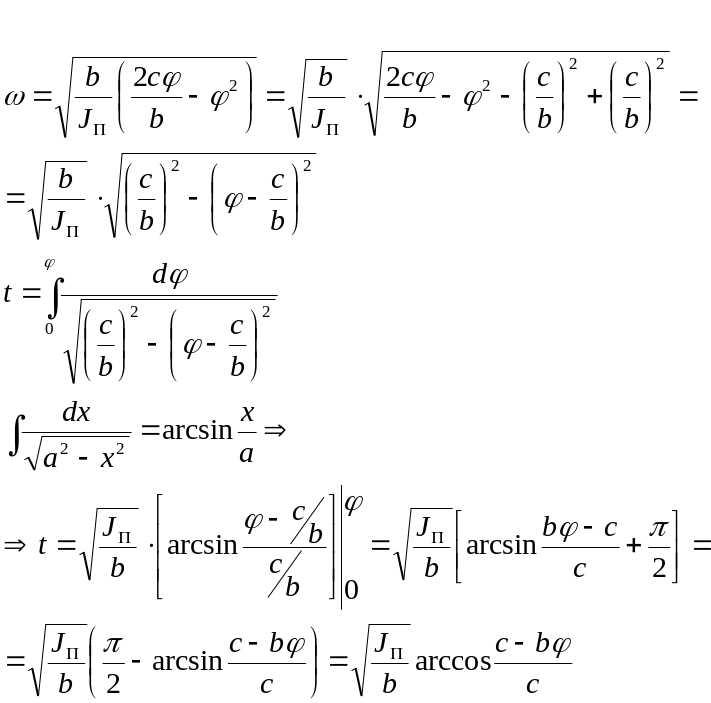
При - время разгона.

Задача ограничения периодических колебаний скорости.

Периодические колебания скорости звена приведения при установившемся движении вызываются двумя основными причинами:

1) Несовпадение законов изменения (силовое возмущение).

2) - переменный характер приведенного момента инерции – инерционное возмущение.

(1)

Равномерное движение возможно, если:

1)

2)

Колебания скорости вызывают переменные нагрузки в кинематических парах, что отрицательно влияет на технологический процесс, поэтому они допускаются лишь в определенных пределах.

Вводится коэффициент неравномерности движения:

(2)

(3)

Одним из способов обеспечить заданный коэффициент неравномерности движения является увеличение инерционности машины путем установки дополнительной маховой массы (маховика).

Из формулы (1) видно, что чем больше , тем меньше . Увеличивая массу, увеличиваем , уменьшаем .

Определение постоянной составляющей приведенного момента инерции машины по заданному коэффициенту неравномерности движения.

- постоянное слагаемое.

- переменное слагаемое.

- приведенный момент вращающихся звеньев.

- искомый момент инерции маховика.

Пусть при имеем

Тогда находим наибольший перепад:

Учитывая, что , имеем:

(1)

(2)

Общий случай.

Метод Н.И. Мерцалова.

- кинетическая энергия в начале цикла.

Так как неизвестная величина не влияет на характер графика, то достаточно построить график

определяется приближенно по средней угловой скорости:

Используем формулы (1) и (2):

График одновременно является приближением графика

Линия проходит посередине отрезка “ab”

Масштабный коэффициент:

2) Частный случай

В точках экстремума , тогда дифференциальное уравнение:

Следовательно, положение определяется точками пересечения графиков

.

(1)

Пример.

Для машины с синусным механизмом определить момент инерции маховика

Движущий момент (принять постоянным). Сила сопротивления (постоянная) и действует в интервале . Переменной составляющей пренебречь.

Решение.

Кинематические характеристики:

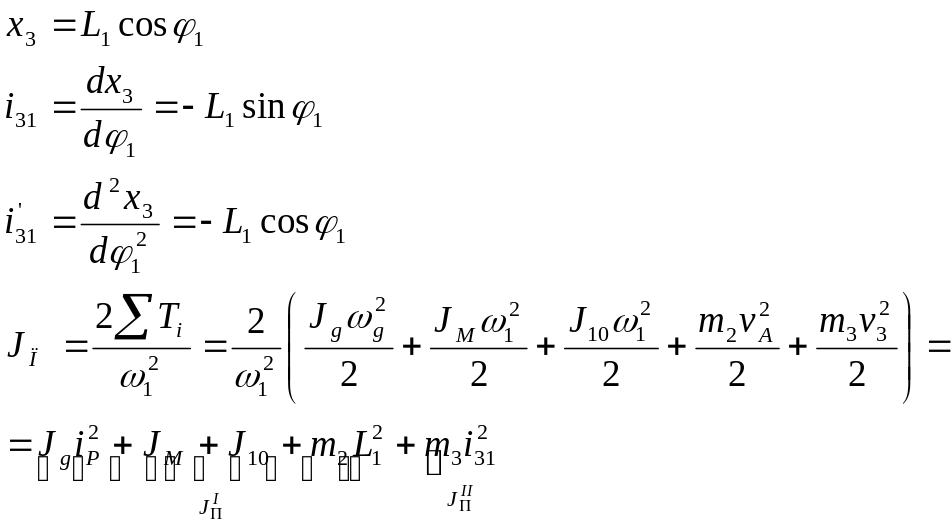
Работа сил сопротивления за цикл:

Работа движущих сил за цикл:

Так как за цикл установившегося движения , то, приравняв, имеем:

Находим углы:

Определение для машины с электроприводом.

Рассмотрим механическую характеристику трехфазного асинхронного электродвигателя переменного тока.

1 – пуск двигателя

2 – критические значения

3 – номинальные значения

4 – холостой ход - синхронная скорость.

2 – 3 – 4 – зона устойчивой работы двигателя.

1 – 2 – зона неустойчивой работы - при выходе на нее двигатель останавливается (опрокидывается).

Устойчивый участок приближенно можно описать в виде прямой линии, проходящей через точки 3 – 4.

- крутизна (жесткость) характеристики.

Рассмотрим случай, характерный для машин ударного действия.

Холостой ход – от ω_min до ω_max

Рабочий ход – от ω_max до ω_min

Дифференциальное уравнение движения для рабочего хода:

Отсюда:

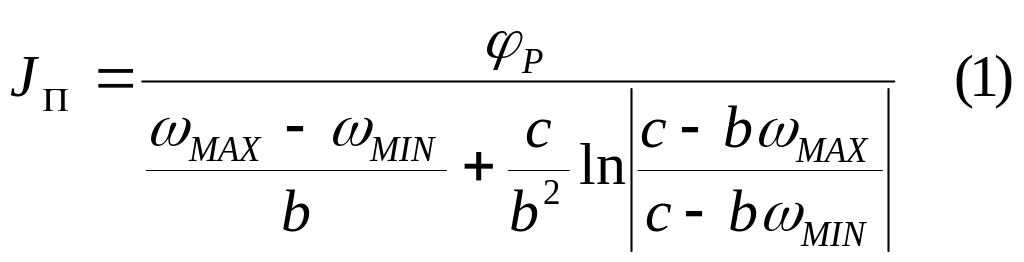
Составляем дифференциальное уравнение движения для холостого хода:

В (1) и (2) три неизвестных:

Задавая , можно найти и

Учет динамической характеристики двигателя.

Характеристика является статической, так как не учитывает инерционности !!!! процессов, связанных с изменением нагрузки во времени.

Для учета этих процессов используется динамическая характеристика в виде:

- электромагнитная составляющая времени.

Переходим к звену приведения.

Уравнение (1) запишем в следующем виде:

Вместе с уравнением (2) рассматриваем уравнение движения звена приведения, которое при!!!

Продифференцируем:

Уравнения (3) и (4) подставим в уравнение (2), учитывая электромагнитную инерцию:

Используем уравнение (5) для определения зависимости при разгоне машины в случае :

, где:

- постоянна.

Составляем характеристическое уравнение:

1) - корни действительные, различные и отрицательные.

При :

Уравнение (8) описывает апериодический процесс.

При - угловая скорость установившегося движения.

2)

Корни

Затухающий процесс.

Такой режим разгона допускать не следует!

Если решать рассматриваемую задачу, исходя из статической характеристики, т.е. при , то выявить колебания при разгоне не удастся. Для этого случая было ранее получено:

3)

Уравнение (10) описывает апериодический неколебательный процесс.

Лекция ХХХ.

Метод кинетостатики. Силы инерции звеньев.

Силовой анализ механизма выполняется методом кинетостатики, который состоит в том, что уравнения движения записываются в форме уравнений равновесия или статики. Для этого к каждому подвижному звену механизма наряду с реально действующими активными силами и реакциями связи прикладываются силы инерции, после чего, на основании принципа Даламбера, составляются уравнения равновесия в следующем виде:

1) Векторная сумма всех сил равна нулю. или

2) Сумма моментов

Силы инерции звена, совершающего плоскопараллельное движение и имеющего плоскость симметрии, параллельную плоскости движения, приводятся к главному вектору , приложенному в центре масс “S” и главному моменту :

- центральный момент инерции.

Силу и момент можно заменить одной силой , приложенной на расстоянии “H” от “S”:

- пара сил

Рассмотрим частные случаи.

1) Поступательное движение звена.

2) Вращательное движение звена вокруг оси, проходящей через центр масс.

3) Вращательное движение вокруг оси, проходящей через центр масс:

Условия статической определимости плоских кинематических цепей.

Рассмотрим действия реакций в различных кинематических парах без учета трения.

- реакция на звено “1” со стороны звена “2”

Условия статической определимости плоских кинематических цепей.

Рассмотрим действие реакций в различных кинематических парах без учета трения:

1) Вращательная пара.

R₁₂ – реакция на звено 1 со стороны звена 2.

2) Поступательная пара.

3) Высшая пара.

Во вращательной паре неизвестны величина и направление реакций, а точка приложения известна (центр шарнира) – неизвестна.

В поступательной паре неизвестны величина и точка приложения, а направление известно.

В высшей паре неизвестна величина, а точка приложения и направление известны.

Таким образом, общее число неизвестных равно:

.

Общее число возможных уравнений равновесия: 3n, n – число подвижных звеньев.

Следовательно, условие статической определимости в кинематической цепи имеет вид:

Для рычажных механизмов p_B = 0, тогда условие:

Этому условию удовлетворяют структурные группы (группы Ассура).

Кинетостатический силовой анализ плоских рычажных механизмов аналитическим методом.

Пример.

Задано:

Закон движения начального звена

Внешняя сила:

Силы тяжести звеньев:

Определить:

Реакции в кинематических парах

(взаимодействие между звеньями)

Решение.

Определяем силы и моменты сил инерции:

Отделяем от механизма статически определимую структурную группу (2,3):

Силы и моменты показываем в положительном положении кроме сил тяжести.

Их истинное направление укажет знак “+” или “-” после числовых расчетов.

находим из уравнения:

для всей группы.

Составляем сумму проекций на ось Х:

находим из уравнения:

для звена “2”.

находим из уравнения:

- для всей группы.

В данном случае проходит через т. В.

Реакцию находим в проекциях и из уравнений:

и - для звена “2”.

Рассчитаем начальное звено “1”:

М_ур – уравновешивающий (движущий) момент, который действует со стороны привода и обеспечивает принятый закон движения.

Имеем:

Статически определимая задача:

Три неизвестных -

Три уравнения равновесия.