
- •Измерительные сигналы
- •Классификация помех
- •Математическое описание измерительных сигналов
- •Периодические и импульсные измерительные сигналы
- •Математические модели элементарных измерительных сигналов
- •Математические модели сложных измерительных сигналов
- •Модулированные сигналы
- •Сигналы с импульсной и импульсно-кодовой модуляцией.
- •Импульсно – кодовая (цифровая) модуляция
- •Основные сведения об импульсной и цифровой технике измерений
Математические модели элементарных измерительных сигналов
Дельта – функция рассмотрим теоретическую модель бесконечно короткого импульса с бесконечно большой амплитудой, аналитически определяемого формулой:
![]()
Площадь такого импульса всегда равна
единице, т.к.
![]() .
.
Функцию
![]() называют дельта-функцией, единичным
импульсом, функцией Дирака, и она имеет
физическую размерность циклической
частоты – с -1.
называют дельта-функцией, единичным
импульсом, функцией Дирака, и она имеет
физическую размерность циклической
частоты – с -1.
При сдвиге дельта-функции по оси времени
на интервал
![]() определения функции можно записать в
общем виде:
определения функции можно записать в
общем виде:
![]() ,
,
![]() .
.
Дельта-функция обладает важнейшим свойством, благодаря которому она получила широкое применение в математике, физике, радио – и измерительной технике.
Пусть имеется некоторая непрерывная
функция времени
![]() .
Тогда, согласно вышеприведенным формулам,
справедливо соотношение:
.
Тогда, согласно вышеприведенным формулам,
справедливо соотношение:
![]()
Это выражение характеризует фильтрующее
(выделяющее, или стробирующее – от слова
«строб» - короткий прямоугольный импульс)
свойство дельта-функции, которое
используется для представления
дискретизированных во времени сигналов
с шагом дискретизации
![]() .
.
Единичная функция. Предельное, упрощенное аналитическое выражение этого сигнала принято записывать так:
![]() .
.
Функцию называют единичной функцией, функцией включения или функцией Хевисайда.
Спектральная плотность гармонического
сигнала. Определим спектральную
плотность сигнала
![]() .
Подставим в прямое преобразование Фурье
заданный сигнал, и, воспользовавшись
формулой Эйлера
.
Подставим в прямое преобразование Фурье
заданный сигнал, и, воспользовавшись
формулой Эйлера
![]() ,
находим:
,
находим:
![]() =
=
![]()
Последнее соотношение можно записать в следующем виде:
=
|
|
=
![]() .
.
Итак, гармоническому (в данном случае
косинусоидальному) сигналу с конечной
амплитудой соответствует дискретный
спектр, состоящий их двух линий бесконечно
большой амплитуды в виде дельта-функций,
расположенных симметрично относительно
нуля на частотах
![]() и
и
![]() .
По аналогии с косинусоидальным сигналом
нетрудно показать, что синусоидальному
сигналу
.
По аналогии с косинусоидальным сигналом
нетрудно показать, что синусоидальному
сигналу
![]() отвечает спектральная плотность
отвечает спектральная плотность
=
![]() .
.
Здесь знак минус – следствие нечетности функции синуса.
Экспоненциальный импульс. Это
сигнал с «полубесконечной» длительностью
и при единичной амплитуде описывается
как
![]() ,
гле
,
гле
![]() - вещественный параметр.
- вещественный параметр.
Постоянный сигнал – самый простой из элементарных сигналов (напряжение, ток).
Математические модели сложных измерительных сигналов
Сигналы с линейными участками. В измерительной технике применяют периодические сигналы с линейными участками. Это линейный знакопеременный и однополярный линейно изменяющийся (пилообразный) сигнал.
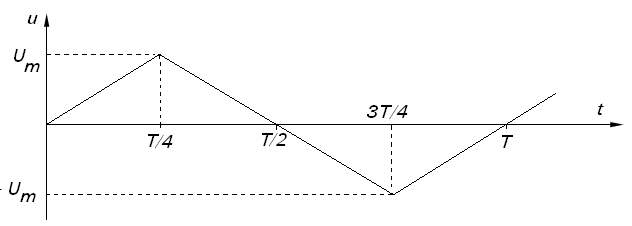
Рис.1 Линейный знакопеременный сигнал
Линейный знакопеременный сигнал описывается уравнениями:
![]()
Модулированные сигналы
В метрологии под модуляцией понимается
процесс, при котором измерительный
сигнал
![]() воздействует
на какой-либо параметр некоторого
стационарного сигнала
воздействует
на какой-либо параметр некоторого
стационарного сигнала
![]() ,
обладающего такой физической природой
и таким характером изменения во времени,
при которых удобны его дальнейшие
преобразования и передача. В качестве
стационарного сигнала именуемого
несущим, обычно выбирают либо
последовательность импульсов, либо
синусоидальное (гармоническое) колебание:
,
обладающего такой физической природой
и таким характером изменения во времени,
при которых удобны его дальнейшие
преобразования и передача. В качестве
стационарного сигнала именуемого
несущим, обычно выбирают либо
последовательность импульсов, либо
синусоидальное (гармоническое) колебание:
![]()
где
![]() -
амплитуда в отсутствии модуляции;
-
амплитуда в отсутствии модуляции;
- угловая (круговая) частота;
![]() - начальная фаза;
- начальная фаза;
![]() - полная фаза.
- полная фаза.
В зависимости от того, какой из параметров гармонического несущего колебания подвергается воздействию, различают амплитудную, частотную, фазовую и ряд видов импульсной модуляции.
Физический процесс, обратный модуляции, называется демодуляции или детектированием, и заключается в получении из модулированного колебания сигнала, пропорционального модулирующему.
Наиболее простым модулированным сигналом
является амплитудно-модулированный
сигнал, в котором измерительная
информация заложена в амплитуду
![]() несущего колебания
несущего колебания
![]() ,
где
,
где
![]() - безразмерный коэффициент пропорциональности.
- безразмерный коэффициент пропорциональности.
Пусть модулирующий сигнал – гармоническое
колебание вида
![]() .
Тогда, приняв для упрощения
.
Тогда, приняв для упрощения
![]() ,
и подставив в формулу для колебания
этот сигнал, получим:
,
и подставив в формулу для колебания
этот сигнал, получим:
![]() ,
где
,
где
![]() –максимальное
отклонение амплитуды АМ – сигнала от
амплитуды несущей
;
–максимальное
отклонение амплитуды АМ – сигнала от
амплитуды несущей
;
![]() –
коэффициент или глубина амплитудной
модуляции.
–
коэффициент или глубина амплитудной
модуляции.
Сигналы с частотной модуляцией.
При частотной модуляции несущая частота
![]() связана
с модулирующим сигналом
зависимостью:
связана
с модулирующим сигналом
зависимостью:
![]() ,
где
,
где
![]() - размерный коэффициент пропорциональности.
- размерный коэффициент пропорциональности.
Рассмотрим однотональную частотную
модуляцию, когда модулирующим колебанием
является гармоническое колебание
![]() .
Тогда, приняв для упрощения
,
определим полную фазу ЧМ сигнала в
любой момент времени
.
Тогда, приняв для упрощения
,
определим полную фазу ЧМ сигнала в
любой момент времени
![]() путем интегрирования частоты, выраженной
:
путем интегрирования частоты, выраженной
:
![]()
где
![]() =
=
![]() - максимальное отклонение частоты от
значения
или девиация частоты при частотной
модуляции.
- максимальное отклонение частоты от
значения
или девиация частоты при частотной
модуляции.
Отношение
![]() ,
являющееся девиацией фазы
несущего колебания, называют индексом
частотной модуляции.
,
являющееся девиацией фазы
несущего колебания, называют индексом
частотной модуляции.
С учетом этого выражения ЧМ сигнал запишется как
![]() =
=
![]() .
.
Фазовая модуляция
При однотональной модуляции фаза несущего колебания
![]()
![]()
где
![]() -
коэффициент пропорциональности;
-
коэффициент пропорциональности;
![]() =
=
![]() - индекс фазовой модуляции.
- индекс фазовой модуляции.
С учетом этого выражения ФМ сигнал запишется как
![]() =
=
![]() .
.
Нетрудно заметить, что ЧМ и ФМ сигналы при однотональной модуляции похожи.
