Теорема Штейнера.

В приведенных примерах оси проходят через центр инерции тела. Мо­мент инерции относительно других осей вращения определяется при по­мощи теоремы Штейнера: момент инерции тела относительно произвольной оси вращения равен сумме момента инерции Jc относительно параллельной оси, проходящей через центр инерции тела, и величины произведения массы тела на квадрат расстояния между ними. где m масса тела, а - расстояние от центра инерции тела до выбранной оси вращения,т.е.

, где m - масса тела, а - расстояние от центра

инерции тела до выбранной оси вращения.

Покажем на одном примере применение теоремы Штейнера. Вычислим момент инерции тонкого стержня относительно оси, проходящей через его край перпендикулярно стержню. Прямое вычисление сводится к тому же ин­тегралу (*),но взятому в других пределах:

Расстояние до оси, проходящей через центр масс, равно а = ℓ/2.По теореме Штейнера получаем тот же результат.

.

§22.Основной закон динамики вращательного движения.

Формулировка закона: Скорость изменения момента импульса относительно полюса равна главному моменту силы относительно того же полюса, т.е.

.

В проекциях на оси координат: .

Если вращение тела происходит относительно неподвижной оси, то основной закон динамики вращательного движения примет вид: . В данном случае момент импульса легко выразить через угловую скорость и момент инерции тела относительно рассматриваемой оси:. Тогда основной закон динамики вращательного движения примет вид:. Если тело не рассыпается и не деформируется, то

, вследствие чего . Если ко всему, тои, оно равно:.

Элементарная работа, совершаемая моментом силы, при вращательном движении относительно неподвижной оси вычисляется по формуле: (*). Полная работа. Если, то.

На основании формулы (*), получим выражение для кинетической энергии вращательного движения твёрдого тела относительно неподвижной оси. Т.к. , то. После интегрирования, получим окончательный результат для кинетической энергии вращательного движения относительно неподвижной оси.

§23.Закон сохранения момента импульса.

Как уже указывалось, законы сохранения энергии и импульса связаны с однородностью времени и пространства, соответственно. Но у трехмер­ного пространства, в отличие от одномерного времени, имеется еще одна симметрия. Пространство само по себе изотропно,в нем нет выделен­ных направлений. С этой симметрией связанзакон сохранениямомента импульса.Эта связь проявляется в том, что момент количества движе­ния, является одной из основных величин, описывающих вращательное движение.

По определению момент импульса отдельной частицы равен .

Направление вектора Lопределяется по правилу буравчика (штопора), а его величина равна L = r p sin ,где

  угол между направлениями радиус-вектора частицы и ее импульса. Величина ℓ = r sinравна рас­стоянию от начала координатОдо прямой, вдоль которой направлен импульс частицы. Эта величина называетсяплечом импульса.ВекторLзависит от выбора начала координат, поэтому говоря о нем, обычно указывают: "момент импульса относительно точкиО".

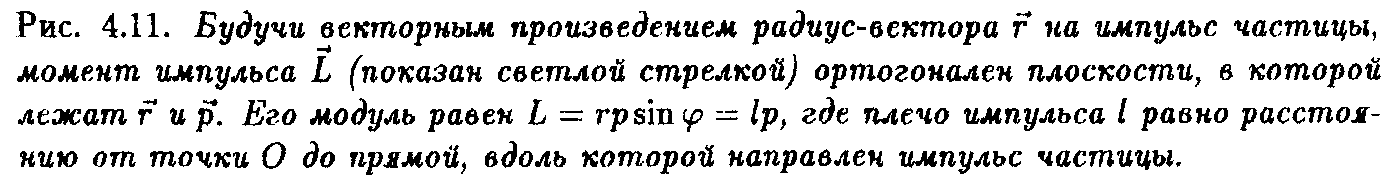
Рассмотрим производную по времени от момента импульса:

.

Первое слагаемое равно нулю, т.к. . Во втором слагаемом, согласно второму закону Ньютона, производную по импульсу можно заменить на действующую на тело силу. Векторное произведение радиус-вектора на силу называетсямоментом силыотносительно точкиО: .

Направление момента силы определяется тем же правилом буравчика. Его величина М = r F sin ,где

•  угол между радиус-вектором и силой. Аналогично тому, как это было сделано выше, определяется и плечо силы

ℓ = r sin — расстояние от точкиОдо линии действия силы. В итоге получаем уравнение движения для момента импульса частицы:.

По форме уравнение аналогично второму закону Ньютона: вместо им­пульса частицы стоит момент импульса, а вместо силы —момент силы. Если,то,т.е. момент импульса постоянен в отсутствие внешних моментов сил.

Формулировка закона: Момент импульса замкнутой системы относительно полюса не изменяется с течением времени.

В частном случае вращения относительно неподвижной оси, имеем: , где

начальные момент инерции и угловая скорость тела относительно рассматриваемой оси, а

конечные момент инерции и угловая скорость тела относительно рассматриваемой оси.

Закон сохранения полной механической энергии с учётом вращательного движения: полная механическая энергия консервативной системы постоянна: .

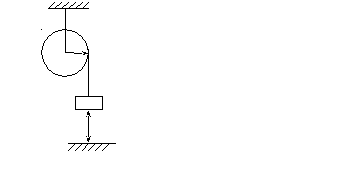
Пример: Найти скорость системы при прохождении расстояния h.

Дано: m, M, h. Найти: V - ?

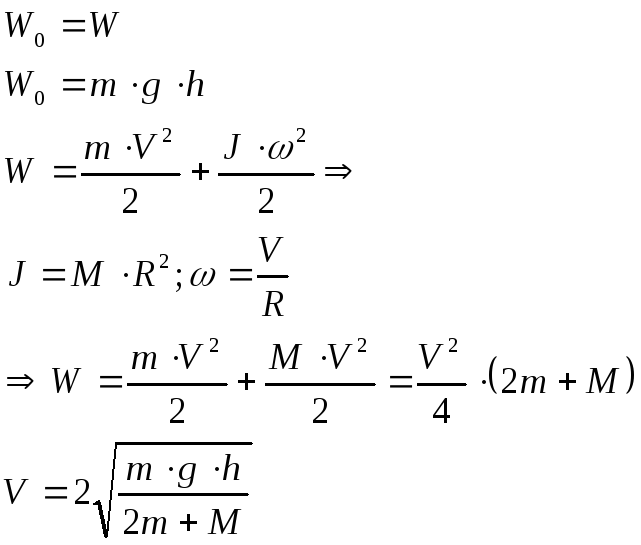
11