§ 12. «Почти все» графы

В этом параграфе приводятся некоторые результаты, характеризующие свойства графов при большом числе вершин, т. е. в асимптотике. Эти свойства формулируются в терминах «почти всех графов» и отражают тем самым типичный случай.

Обозначим через (n) множество всех помеченных простых графов с множеством вершин V = {1, 2, ..., n}.

Как отмечалось в § 1, |(n) | = .

П усть P — некоторое свойство, которым каждый отдельно взятый граф из (n) может обладать или не обладать. Через P(n) обозначим множество тех графов из (n), которые обладают свойством Р. Будем говорить, что почти все графы (почти каждый граф) обладают свойством P, если

и почти нет графов, обладающих свойством P, если

Ясно, что если почти все графы обладают свойством P, то почти нет графов, не обладающих свойством P.

К настоящему времени получены результаты о большом количестве свойств графов в терминах «почти всех графов». Приведем некоторые из этих результатов.

Теорема 12.1. Почти все графы связны.

> Обозначим через _СВ(n) множество связных графов из (n), а через _s(n)— множество тех графов из (n), в каждом из которых имеется по крайней мере одна компонента порядка s. Тогда справедливо неравенство

Далее рассмотрим следующий прием построения графов:

1) множество V разбиваем на подмножества V₁ и V₂,

где |V₁| = s, |V₂| = n — s (таких разбиений имеется );

2) образуем всевозможные графы на множестве вершин V₁ и всевозможные графы на множестве вершин V₂.

В результате второй операции получим

р азличных графов. Резюмируя, имеем

Т ак как |(n)| = , то из неравенств (1) и (2) следует, что

г де

Р ассматривая отношение f(s+1)/f(s), убеждаемся в том, что на отрезке [1, [n/2]] функция f(s) убывает. Поэтому

откуда на основании (3) заключаем, что теорема 12.1 верна. <

Теорема 12.2. Диаметры почти всех графов равны 2.

Для доказательства этой теоремы понадобится следующее очевидное

Утверждение 12.3. Число всех графов из (n), в каждом из которых зафиксированы одни и те же r ребер и одновременно отсутствуют k других фиксированных ребер, равно .

> Доказательство теоремы 12.2. Прежде всего заметим, что диаметр почти каждого графа не меньше 2, поскольку только полный граф имеет диаметр 1.

Теперь убедимся, что диаметр почти каждого графа не может быть больше 2. В множестве V фиксируем вершину v₁ и непустое подмножество UV, удовлетворяющее следующим двум условиям: 1) v₁U; 2) r=|U|<= n — 2. Положим W =V \(Uv₁) и выберем вершину vW. Рассмотрим множество _Uv1v(n) всех графов из (n), в которых окружение вершины v₁ совпадает с U, а вершина v не смежна ни с какой вершиной из U. Для графов из этого множества есть r обязательных ребер и n — 1 запрещенных. Согласно утверждению 12.3

Д ля выбора вершины v в множестве W есть n — r— 1 возможностей. Если теперь

т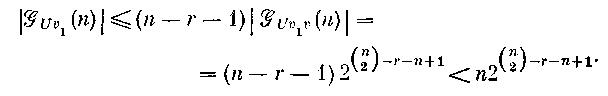 о

П усть, далее,

где в качестве U фигурирует каждое из подмножеств множества V, удовлетворяющее указанным выше условиям 1) и 2). При фиксированном r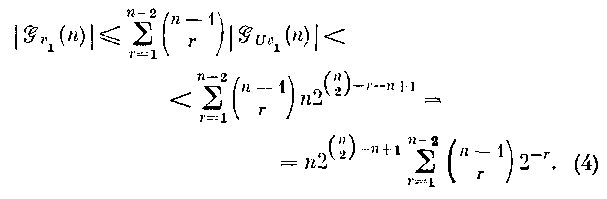 = |U| для выбора множества U есть вариантов, поэтому

Д алее используем формулу бинома Ньютона: для любых чисел a и b и натурального n верно равенство

( здесь = 1). Согласно этой формуле

П оэтому из (4) вытекает

О бозначив

и меем

Д алее получаем

В то же время легко видеть, что если "(n) — множество графов с диаметром более 2, то "(n)'(n). Действительно, возьмем произвольный n-вершинный граф G, диаметр которого не менее 3. В нем существуют хотя бы две вершины v₁ и v, расстояние между которыми равно трем. Очевидно, что G_Uv1v(n), где U = N_G(v₁), Поэтому " (n)'(n). Итак, почти нет графов с диаметром более 2, что и доказывает теорему. <

Следствие 12.4. Радиус почти каждого графа совпадает с диаметром этого графа и равен 2.

> Очевидно, что r(G)<=d(G) для любого графа G. Поэтому достаточно показать, что почти нет графов радиуса 1. Рассмотрим множество '(n) графов из (n), в которых степень фиксированной вершины v равна n — 1. Имеем

откуда получаем, что число графов из (n), максимальная степень вершин которых равна n — 1, не превосходит числа . Но это означает, что почти нет графов, среди вершин которых есть хотя бы одна доминирующая. Поэтому почти нет графов радиуса 1, так как всякий граф радиуса 1 содержит хотя бы одну доминирующую вершину. <

Теорема 12.5. Почти все графы имеют единственную вершину максимальной (минимальной) степени.

Теорема 12.6. Группа автоморфизмов почти каждого графа совпадает с единичной группой.

Доказательства этих теорем можно найти, например, в обзоре [21].