2.15. Линейные операторы

Оператор (действующий из векторного пространства в векторное же) называется линейным однородным (или просто линейным), если он обладает следующими свойствами:

1. может применяться почленно к сумме аргументов:

;

2. скаляр (постоянную величину) с можно выносить за знак оператора:

.

Из 2) следует, что для линейного однородного оператора справедливо свойство L(0) = 0.

Примеры линейных однородных операторов:

– оператор дифференцирования: ;

– оператор интегрирования: ;

– оператор умножения на определённую функцию : ;

– оператор интегрирования с заданным «весом» : ;

– оператор взятия значения функции в конкретной точке ;

– оператор умножения вектора на матрицу: .

Оператор называется линейным неоднородным, если он состоит из линейного однородного оператора с прибавлением некоторого фиксированного элемента:

,

где — линейный однородный оператор.

2.16. Сюрьективное отображение (сюрьекция)

Рассмотрим отображение , в котором область значений совпадает с областью прибытия. В таком отображении каждый образ имеет хотя бы один прообраз: . Такое отображение называется сюрьективным или сюрьекцией. Геометрическая интерпретация сюрьективного отображения приведена на рис. 2.16.

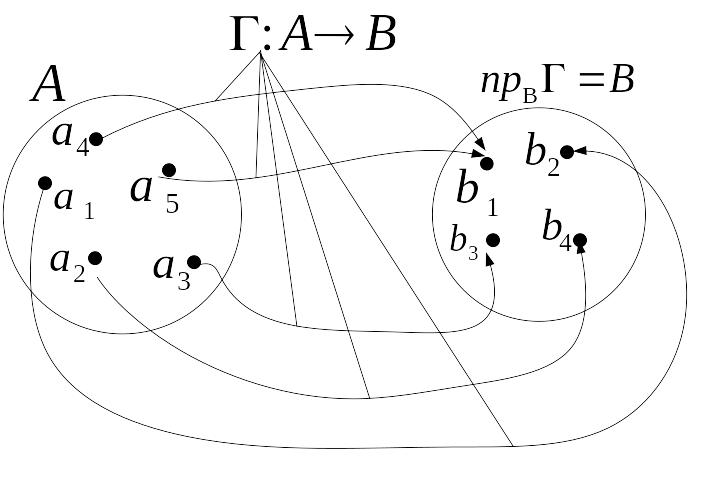
Рис.2.16. Сюрьективное отображение

2.17. Инъективное отображение (инъекция)

Рассмотрим отображение , в котором каждый элемент имеет в точности один образ: , где количество элементов множества . При этом ничего не говорится, совпадает область значений с областью прибытия или нет. Геометрическая интерпретация инъективного отображения приведена на рис. 2.17.

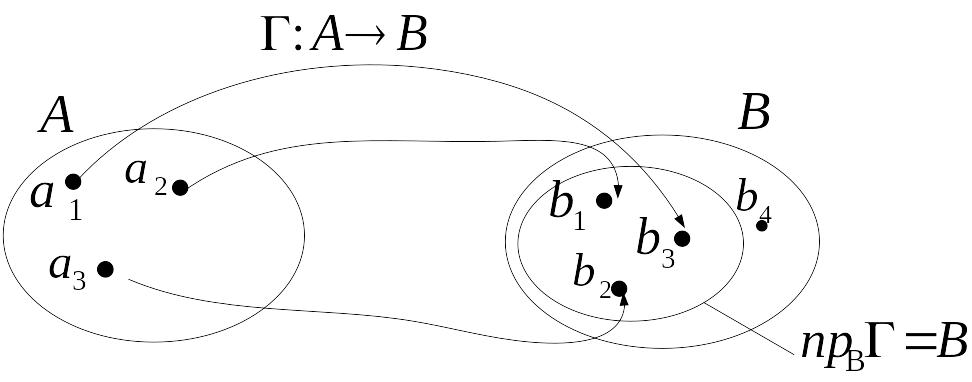
Рис. 2.17. Инъективное отображение

2.18. Биективное отображение (биекция)

Отображение называется биективным, если оно одновременно и сюрьективно и иньективно. Для биективного отображения выполняются условия: , (рис. 2.18).

Рис. 2.18. Сюрьективное отображение

2.19. Отношения

Математическое понятие «отношение», так же как понятие множества, является очень широким и общим. Рассмотрим отображение , . Допустим, что множество совпадает с множеством : . Тогда имеем отображение, заданное на одном множестве.

, , . В этом случае говорят, что на множестве задано отношение . Отношение – всюду определённое соответствие между равными множествами. Отношения, заданные на некоторых числовых множествах, могут выражаться терминами «быть равным», «быть больше», «быть меньше», «быть делителем» и т.д. Отношение во множестве линий на плоскости могут выражаться терминами «быть параллельными», «пересекаться», «касаться» и т.д. Ранее нами рассматривалось отношение композиции отображений, соответствий, заданное на множествах. Отношение является частным случаем отображения, когда область определения и множество значений совпадают, поэтому всё сказанное ранее для отображений справедливо и для отношений.

В отображении множество может представлять собой декартову степень . В этом случае имеем отношение . Показатель декартовой степени называется арностью отношения. Если в отношении показатель декартовой степени равен единице ( , то имеем унарное отношение . Таким образом, унарное отношение, заданное на множестве, представляет собой некоторое подмножество этого множества. Унарное отношение называют ещё свойством. Элементами унарного отношения являются элементы множества, на котором задано это отношение. Если показатель степени равен двум ( , то отображение называется бинарным . Элементами бинарного отношения являются упорядоченные пары. Высказывательная форма бинарного отношения имеет вид:

.

Если показатель степени равен трём ( , то отображение называется тенарным. Элементами тенарного отношения являются упорядоченные тройки:

^.

Примером тенарного отношения может быть отношение «образовать сумму», которое имеет смысл для троек чисел и выполняется в том случае, когда .

Так можно задать четырёх-арное, пяти-арное, …, арное отношение.

Примером четырёх-арного отношения может быть отношение «пропорциональность», элементами которого являются упорядоченные четвёрки , для которых .

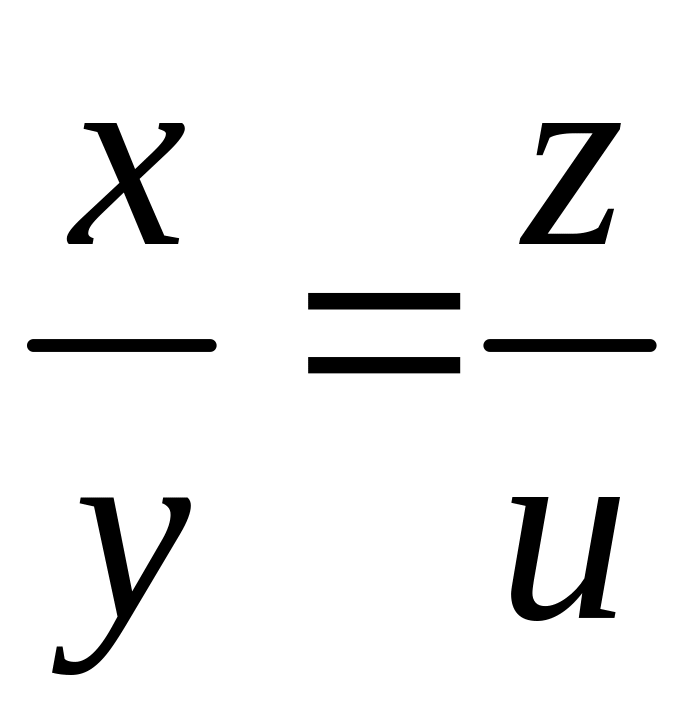Элементами арного отношения являются упорядоченные :

.

Отображение , являющееся функциональным, называется местной операцией. Очевидно, что любая местная операция является арным отношением , но не наоборот, не всякое арное отношение является местной операцией.

арные отношения рассматриваются в информационных технологиях, а именно, в базах данных. Приведём пример арных отношений.

Пример 2.18

В целях разработки информационной системы, учитывающей данные о ходе учебного процесса, описать формально следующую ситуацию.

В университете на экономическом факультете учатся студенты Иванов, Петров, Сидоров. Лекции им читают преподаватели Ковалёв, Резников, Ткачёв. Причём, известны следующие факты.

1. Ковалёв читает лекции по математике и базам данных, 40 и 80 часов за семестр.

2. Резников читает лекции по экономике, 50 часов в семестр.

3. Ткачёв читает лекции по математике и менеджменту, 51 час.

4. Студент Иванов посещает лекции по математике у Ткачёва и по базам данных у Ковалёва.

5. Студент Петров посещает лекции по математике у Ковалёва и у Резникова по экономике.

6. Студент Сидоров посещает лекции по экономике у Резникова и по базам данных у Ковалёва.

Для формального описания данной ситуации, введём три множества:

- множество преподавателей

;

- множество предметов

;

- множество студентов

.

Имеющиеся факты можно разделить на две группы:

1 группа – факты о преподавателях;

2 группа – факты о студентах.

Для того, чтобы отразить факты, характеризующие преподавателей и читаемые ими лекции, введём тенарное отношение , где множество рациональных чисел. Рассмотрим высказывательную форму декартова произведения:

.

Но , т.е. не все упорядоченные тройки принадлежат отношению . Этому отношению будут принадлежать только те упорядоченные тройки , которые отображают тот факт, что преподаватель читает лекции по предмету в количестве часов . Назовём такое отношение «Читает лекции по…». Множество кортежей, образующих отношение удобно представить в виде табл. 2.2.

Таблица 2.2