WSM-wyk. 4_ Reg-korel Podstawy analiz statystycznych - regresja i korelacja Prof. J. Kordos

IV. Analiza regresji I korelacji

4.1. Analiza regresji.

Powstaje problem, czy nie istnieje jakaś metoda umożliwiająca, chociaż w przybliżeniu, przewidzieć wielkość jednej cechy na podstawie znajomości drugiej. A gdyby taka metoda istniała, to powstaje pytanie jak dobre jest to przybliżenie, z jakim przewidujemy wartość jednej cechy, w oparciu o znajomość wartości drugiej cechy. Ta problematyka stanowi przedmiot metody statystycznej zwanej analizą regresji.

Rozważmy populację badaną na dwie cechy X i Y, ale takie, o których wiadomo, że jedna z nich X, wywiera wpływ na drugą Y. Zależności te, jak i wiele innych, nie mają jednak charakteru zależności funkcyjnych lecz tzw. zależności stochastycznych.

Wynika z tego, że mimo niewątpliwego wpływu jednej cechy na drugą, jednej i tej samej wartości cechy X, odpowiadać mogą różne wartości cechy Y.

Tak wiec, zależność między wartością cechy X i Y dla i-ej jednostki wylosowanej z próby, można zapisać w postaci:

Y_i = f(X_i) + e_i (4.1)

Zwykle postaci funkcji f(X) nie znamy. Dlatego dokonujemy jej oceny na podstawie obserwacji próby. Ograniczymy się tu do przypadku funkcji liniowej, wtedy wzór (4.1) przyjmuje postać:

Y_i = a_o + a₁X_i + e_i (4.2)

Równanie (4.2) nazywamy równaniem regresji liniowej.

Podstawowym celem analizy regresji jest oszacowanie nieznanych parametrów a_o i a₁ w oparciu o znajomość n-elementowej próby, która dostarcza informacji a wartościach cechy X i Y w poszczególnych elementach próby, tj.:

(4.3)

Mając oszacowanie parametrów a_o i a₁, można będzie przewidywać, czyli dokonywać prognozy, jaką wartość prawdopodobnie przybierze cecha Y, w przypadku określonej wartości cechy X.

Jeśli przez a_o oznaczymy oszacowanie parametru a_o i przez a₁ oszacowanie parametru a₁ , a przez przewidywaną wartość cechy Y, odpowiadającą i-tej obserwacji, to otrzymamy równanie:

(4.4)

Powyższy wzór jest równaniem regresji z próby.

Do szacowania parametrów a_o i a₁ stosuje się tzw. metodę najmniejszych kwadratów¹. Pomijamy tu zagadnienia związane z zastosowaniem tej metody, a ograniczymy się tylko do podania ostatecznych wzorów na obliczenie parametrów a_o i a₁.

(4.5)

Podamy przykłady zastosowania powyższych wzorów w praktyce.

Niżej zostaną podane przykładowo sumy potrzebne do obliczenia współczynników regresji a_o i a_1.

Podstawiając otrzymane wyniki do wzorów (4.5), ostatecznie dostajemy:

Są to oszacowania współczynników regresji a_o i a₁ z równania regresji (4.4). Możemy na tej podstawie napisać równanie regresji z próby:

= -1,803 +0,962 x_i (4.6)

Tablica 4.1. Rachunki dla obliczenia współczynników regresji a_o i a_1.

Nr Obserwacji i	xi	yi	xiyi	x^2i	y^2i
1.	3	1	3	9	1
2.	5	3	15	25	9
3.	6	4	24	36	16
4.	4	3	12	16	9
5.	7	5	35	49	25
6.	9	6	54	81	36
7.	8	5	40	64	25
8.	8	7	56	64	49
9.	10	8	80	100	64
10.	12	9	108	144	81
11.	13	11	143	169	121
12.	15	13	195	225	169
13.	19	15	285	361	225
14.	21	19	399	441	361
15.	24	20	480	576	400
16.	27	24	648	729	576
17.	27	25	675	729	625
18.	29	27	783	841	729
19.	32	30	960	1024	900
20.	35	31	1085	1225	961
Sumy	314	266	6080	6908	5382

Równanie regresji (4.6) pozwala przewidywać z pewnym przybliżeniem, jaką wartość przybierze cecha Y, jeśli zaobserwowana wartość cechy X będzie równa x_i. Na przykład, gdyby cecha X przyjęła wartość 10, to na postawie równania regresji (4.6) należy oczekiwać, że cecha Y przybierze wartość 7,817. Powstaje pytanie, jak dobre jest to przybliżenie? Miarą ryzyka błędu przewidywania będzie zmienność wartości y_i wokół oszacowań .

Przydatny jest tu tzw. błąd standardowy przewidywania.

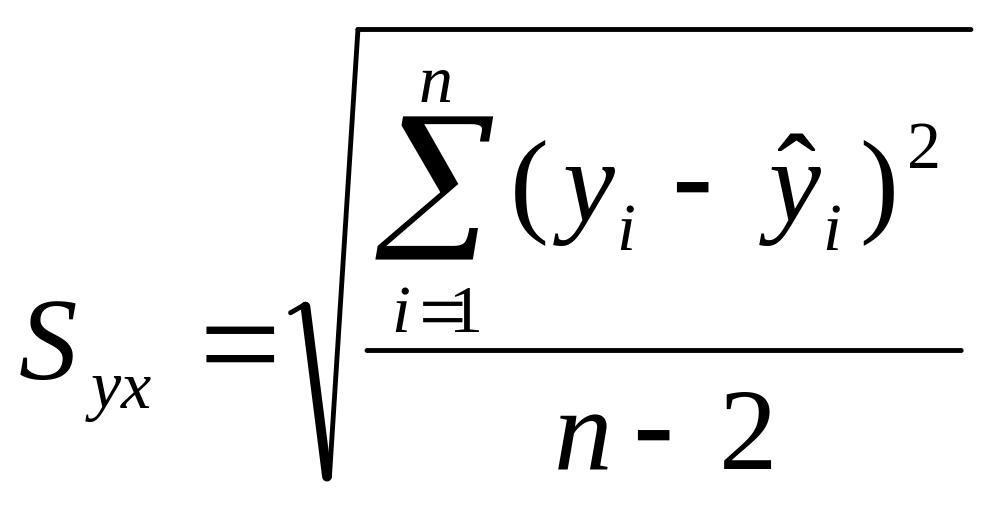(4.7)

Wzór (4.7), po podstawieniu pod wyrażenia (4.4) i po uproszczeniach, przyjmuje postać wygodną dla rachunków:

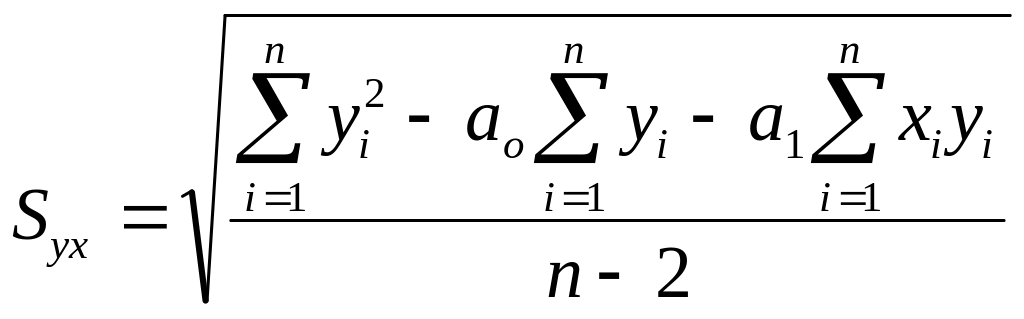(4.8)

W przypadku rozpatrywanej przez nas populacji, na podstawie danych z tablicy 4.1, błąd standardowy przewidywania jest

.

Inną miarą jakości prognozy jest tzw. współczynnik determinacji. Pominiemy jego wyprowadzenie, a podamy już gotowy wzór:

(4.9)

Dla celów rachunkowych wygodnie jest powyższy wzór przedstawić w następującej postaci:

(4.10)

Po podstawienie odpowiednich liczb z tablicy 4.1 oraz wykonaniu działań uzyskamy:

Powyższy wynik można zinterpretować w ten sposób, że 99,3% zaobserwowanej zmienności cechy Y jest wyjaśnione oddziaływaniem cechy X na cechę Y. Pozostałe 0,7% jest niewyjaśnione i przypisujemy je działaniom czynników losowych.

Zajmowaliśmy się wyżej tylko badaniem dwóch cech. Jednakże analiza regresji może być uogólniona na więcej niż dwie cechy. Wówczas badamy wpływ k cech: x₁, x₂,..., x_k, na cechę Y, a równanie regresji liniowej, analogicznie do (11.2) ma postać:

(4.11)

Jest to model wielorakiej regresji liniowej , gdzie wskaźnik i przy poszczególnych cechach oznacza numer obserwacji w próbie dla i = 1, 2,..., n. Nie będziemy się jednak tym modelem tu zajmowali.

Podamy niżej przykład schematu obliczeń parametrów regresji liniowej wraz z interpretacją uzyskanych wyników. Na ćwiczeniach będą podawane zadania w postaci sum cząstkowych potrzebnych do szacowania parametrów strukturalnych równania regresji liniowej.

Przykład.

Oszacować liniową funkcje regresji opisującą zależność płacy (y_i w tys., zł) od stażu pracy (x_i w latach). Zinterpretować współczynnik regresji oraz dokonać predykcji dla x_i = 2,0.

Obserwacja i
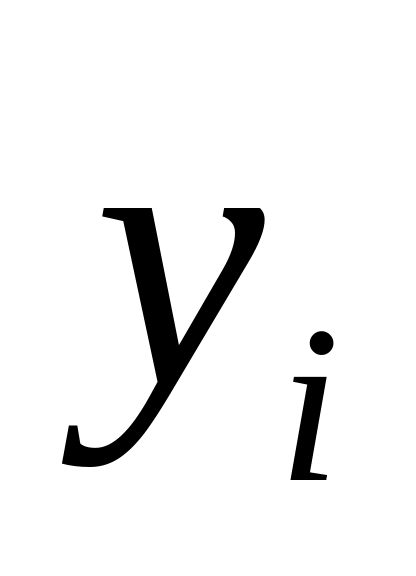
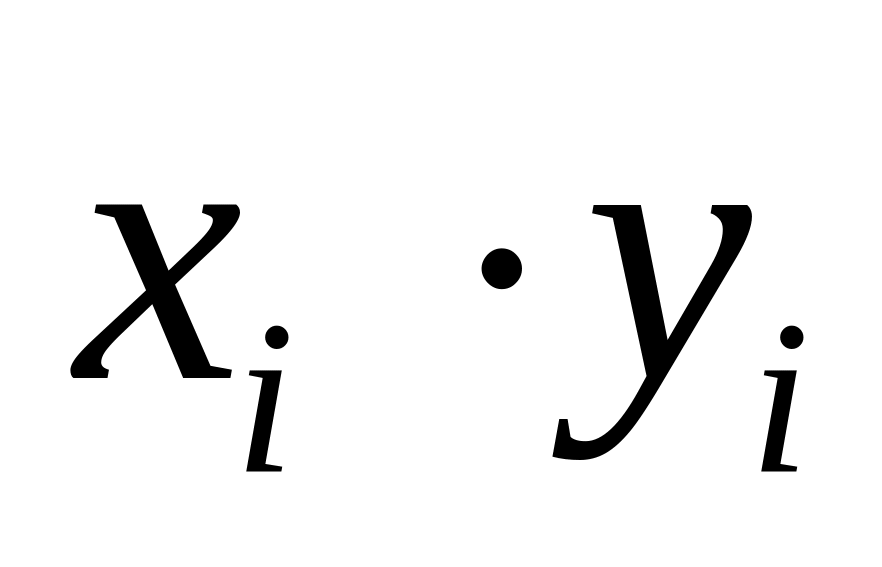
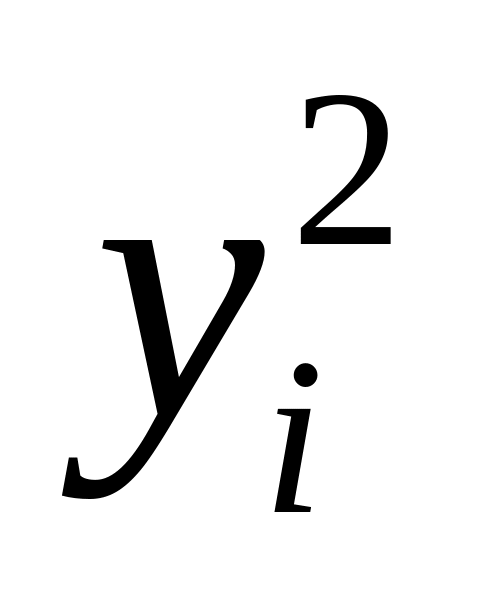
1	1,8	23	41,4	3,24	529
2	1,8	12	21,6	3,24	144
3	0,8	9	7,2	0,64	81
4	1,5	18	27	2,25	324
5	2,2	20	44	4,84	400
6	1,1	10	11	1,21	100
7	1	8	8	1	64
Suma	10,2	100	160,2	16,42	1642

Szacujemy parametry regresji: :

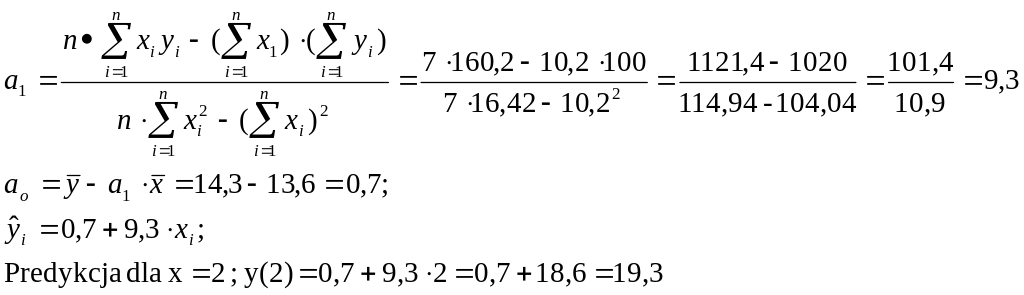
Odpowiedź:

Liniowa funkcja regresji opisującą zależność płacy od stażu pracy przyjmuje postać: współczynnik regresji wynoszący 9,3 oznacza że, przeciętnie rzecz biorąc, 1 rok pracy zwiększa przeciętne płace o 9,3 tys. zł.