4.3. Вероятности ошибки байесовского классификатора.

Рассмотрим случай двух классов ₁ и ₂ (Рис.4.1).

Если рассмотрим пространство одного признака, то решающее правило g(x) порождает разбиение на области принятия решения ₁^* и ₂^*, границей между которыми служит точка на оси признака. Очевидно, что возможны два вида ошибок классиыикации:

1. когда наблюдаемое значение х попадает в область ₂^*, в то время как истинная принадлежность х₁,

2. и наоборот, когда наблюдаемое значение х попадает в область ₂^*, в то время как истинная принадлежность х₂.

Данные события не могут произойти одновременно и составляют полную группу событий. Поэтому вероятность ошибки есть величина

Согласно рисунку, вероятность ошибки P₀ достигает минимума при смещении границы решения из положения 1 в положение 2, когда “хвосты” распределений не перекрываются. Поэтому выгоднее предположить, что

x₁^* при p(₁)p(x|₁)>p(₂)p(x|₂) b x₂^* при p(₁)p(x|₁)p(₂)p(x|₂).

Именно такой выбор и достигается байесовским решающим правилом. Отношение правдоподобия также непосредственно следует из данных выражений. Тогда граница х^* в положении 2 областей ₁^* и ₂^* определяетcя условием p(₁)p(x^*|₁_=p(₂)p(x^*|₂).

Рис.4.1. Вероятности ошибок.

Для случая классификации на два класса проследим аналогию с видами ошибок при проверке гипотез в математической статистике. Очевидно, что совместное распределение p(₁,x) играет роль плотности распределения при справедливости нулевой гипотезы H₀ (класс ₁), а совместное распределение p(₂,x) играет роль плотности распределения при справедливости альтернативной гипотезы H₁ (класс ₂). Тогда первая ошибка классификации – это ошибка первого рода, когда нулевая гипотеза H₀ отвергается, являясь справедливой, с вероятностью .

Вторая ошибка классификации является ошибкой второго рода, когда принимается нулевая гипотеза H₀, являясь неверной, с вероятностью .

Отсюда мощность критерия проверки гипотезы H₀ есть вероятность того, что ошибка второго рода не будет допущена.

4.4. ФОРМИРОВАНИЕ РЕШАЮЩЕГО ПРАВИЛА КАК ОБУЧЕНИЕ РАСПОЗНАВАНИЮ ОРАЗОВ.

Итак, для решения задачи классификации необходимо сформировать некоторое решающее привило отнесения предъявленного объекта х к одному из заранее заданных классов и при этом “не слишком часто ошибаться”.

Будем полагать, что для формирования решающего правила в нашем распоряжении имеется так называемая обучающая совокупность – множество объектов _j, j=1,,N, представленных своими наблюдениями x_j, j=1,,N.

Задача формирования решающего правила по обучающей совокупности рассматривается как задача обучения распознаванию образов, в предложении, что в обучающих наблюдениях содержится достаточно информации для того, чтобы научиться распознавать их принадлежность к некоторым классам или образам.

В зависимости от вида доступной информации различают задачи обучения распознаванию образов с учителем, без учителя (самообучение, автоматическая классификация) и промежуточные варианты обучения.

При обучении с учителем предполагается, что обучающие наблюдения х представлены в паре с указанием класса (х_j,g_j), j=1,,N, где g_j={₁,,_m} – истинный класс j-го наблюдения. Предполагается, что в роли учителя выступает, например, эксперт, оценивающий “истинную” принадлежность объекта к некоторому классу на основании личного опыта и интуиции. Обычно объекты обучающей совокупности являются для эксперта представителями некоторых, не обязательно визуально наблюдаемых, возможно, только мысленных образов, которые он характеризует, как правило, на качественном уровне. Как правило, такие характеристики трудно формализовать. Это означает, что эксперт, скорее всего, затруднится строго формально объяснить, чем различаются представители разных образов, и в чём похожи представители одного образа. Как правило, эксперту значительно проще просто указать принадлежность объектов к обучающим образам. При обучении без учителя нет указаний на классы обучающих объектов. И наконец, классы могут быть указаны лишь для части обучающих объектов.

Качество решающего правила содержательно понимается как частота правильных решений о классе объекта и формализуется с введением вероятностной меры на множестве . Тогда решающее правило должно минимизировать вероятность ошибки неправильной классификации P₀=p[g(x)g()], g(x),g(){₁,,_m}, где g(x) – решение о классе объекта х, g() – истинная принадлежность к некоторому классу.

С другой стороны, качество оценивается средним риском ошибки распознавания – математическим ожиданием потерь от несовпадения предполагаемого и истинного классов объекта R[g()]=M{[g(x),g()]}/

Как было показано, такие оценки качества приводят к байесовскому (оптимальному) решающему правилу вида и основаны на следующих свойствах совместного дискретно=непрерывного распределенияp(_k,x), k=1,,m, в пространстве признаков. Очевидно, что

, где p(_k,x)=p(_k)p(x|_k)=p(x)p(_k|x)/

Тогда априорная вероятность появления класса есть

, к=1,,m,

и условная по классу плотность распределения значений вектора признаков есть

, к=1,,m.

С другой стороны, полное распределение вероятностей в признаковом пространстве есть

,

и апостериорная вероятность появления класса (степень достоверности) есть

, к=1,,m.

Но полные вероятностные характеристики данных часто неизвестны. Поэтому для построения решающего правила их требуется оценить по обучающей выборке. Часто условную плотность распределения p(x|_к) невозможно получить аналитически. Поэтому ограничиваются некоторым простым параметрическим свойство распределений, определяющим параметрический класс решающих правил вида g(x,c), где с – вектор параметров. Тогда для случая двух классов ₁ и ₂ часто решающее правило в виде разделяющей (дискриминантной) функции

.

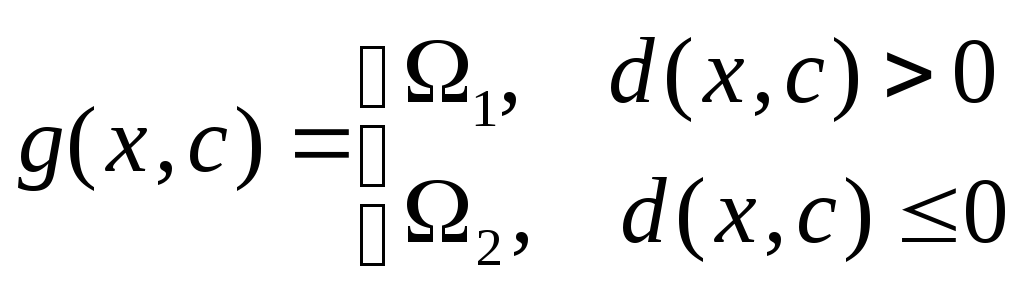Как правило, разделяющая функция является линейной или полиномиальной, гдеy_s(x) является, как правило, s-м членом разложения разделяющей функции d(x,c) в ряд по некоторой системе функций.

Полиномиальная разделяющая функция d(x,c) не является линейной в исходном n- мерном пространстве признаков Х_j, j=1,,n. Но совокупность значений y_s(x), s=1,,p рассматривается как новые признаки Y_s объекта х, посредством которых осуществляется переход в новое p- мерное пространство. Такое пространство называется “спрямляющим”, так как разделяющая функция в нём линейна.

После выбора параметрического семейства решающих правил обучение понимается как поиск вектора параметров, обеспечивающего наименьший средний риск ошибки распознавания.

Предположим, что условные плотности распределения p(x|_k), k=1,,m целиком сосредоточены в некоторых областях признакового пространства ₁,,_m таких, что их выпуклые оболочки не пересекаются. Тогда для каждой пары разных классов существует линейная разделяющая функция, безошибочно классифицирующая объекты этих двух классов. Такую постановку задачи обучения называют детерминистской. Разделяющая функция определяется лишь формой примыкающих друг к другу непересекающихся областей признакового пространства и не зависит от конкретного вида их распределения вероятностей. С геометрической точки зрения разделяющая функция в многомерном признаковом пространстве определяется уравнением разделяющей гиперповерхности, в частности, линейная функция является разделяющей гиперплоскостью.

Рассмотрим основные классические постановки задачи обучения распознаванию образов в рамках вероятностного подхода.