2.10. Теоретико-информационный подход.

Одна из современных трактовок понятия связи состоит в том, что некоторые признаки X и Y связаны, если известное значение признака Y уменьшает неопределенность в получении значения признака Х. В свою очередь, уменьшение неопределенности всегда связано с получением некоторого количества информации. Неопределенность в самом общем смысле понимается как разнообразие некоторого множества, в частности множества значений некоторого признака. Тогда получение информации понимается как ограничение разнообразия. Ограничение разнообразия возникает, например, когда разнообразие, существующее при одном условии, меньше чем разнообразие, существующее при другом условии.

Измерение связи между двумя признаками X и Y состоит в измерении сопряженного (совместного) разнообразия системы (X,Y), когда измеряется ограничение наблюдаемого разнообразия признака Х в системе (X,Y) по сравнению с его разнообразием отдельно от признака Y.

В этом смысле мера связи признаков должна не только оценивать степень отклонения их совместного распределения от независимости, но и характеризовать возможность прогноза значений одного признака по значениям другого.

Очевидно, что самый точный прогноз по таблице сопряженности возможен, когда по некоторому значению y_j признака Y можно однозначно определить некоторое значение x_i признака Х. В этом случае признак Y однозначно соответствует признаку Х. Если, в свою очередь, признак Х однозначно соответствует признаку Y, то они находятся во взаимооднозначном соответствии. Такая ситуация означает полную связь, и ей соответствует максимальное значение меры связи. Очевидно, что такая мера связи в общем случае несимметрична (Рис.2.4).

а) б)

		*			*
			Х	*			Х
*	*					*

Рис.2.4. а) однозначный прогноз Х по Y; YX.

б) взаимно-однозначный прогноз Y X.

С другой стороны, отсутствие связи традиционно означает статистическую независимость признаков Х и Y. Но, вообще говоря, существует возможность удовлетворительного прогноза значений одного признака по значениям другого и в случае их статистической независимости. Поэтому отсутствие связи понимается как максимальная несвязанность признаков, которая достигается лишь при определенных условиях для статистически независимых признаков и означает полное отсутствие возможности прогноза.

При конструировании мер связи различных признаков, в частности номинальных, предполагается, что нулевое значение говорит об отсутствии связи. С другой стороны, удобно, чтобы верхний предел, означающий полную связь, был равен 1. Часто нормированные меры связи строятся как отношения

U(X) – неопределенность признака Х в отдельности, U(X/Y) – неопределенность Х при значении Y.

Все многообразие мер связи такого типа связано с конкретным определением понятия неопределенности.

Пусть Х – признак, принимающий значения х₁, …x_r c маргинальными вероятностями p_1,…p_r, a Y - признак, принимающий значения y₁, …y_r c маргинальными вероятностями p_1,…p_s. Пусть (р)>0 – некоторая невозрастающая функция, определенная на интервале 0р1, где (1)=0. Пусть функция (р) имеет смысл оценки значения неопределенности, возникающей при измерении признака Х, если был реализован исход х_i c вероятностью p_i. Тогда средняя ожидаемая неопределенность в одном измерении признака Х есть величина Очевидно, что эта величина равна нулю, если был реализован только один исход с вероятностью p_i =1. Тогда условная неопределенность выражается как величина

где, согласно теореме умножения вероятностей p_ij=p_jp_i/j, и - условное дискретное распределение признака Х при некотором известном значении признака Y=y_i.

Если принять (р)=-log p, то неопределенность признака Х выражается как величина

где H(X) и H(X/Y) представляют собой энтропию и условную энтропию признака Х. Понятие энтропии было введено в работах К.Шеннона в 1948 г., посвященных проблемам передачи информации.

Нормированная мера связи является коэффициентом нормированной информации. При этомR(X/Y)=0 для статистически независимых признаков, так как

В то же время R(X/Y)=1 при полной связи. В этом случае условное распределение p_i/j , i=1,…r признака Х для некоторого значения y_i сосредоточено только в одном некотором значении х_k, то есть p_i/j =1, i=k и p_i/j =0, ik, i=1,…r. Тогда выполнено

Пусть (p)=1-p и имеет смысл вероятности ошибки прогноза некоторого значения, появление которого ожидается с вероятностью p. Тогда средняя вероятность ошибки прогноза есть величина

Средняя условная вероятность ошибки прогноза есть величина

Относительное уменьшение вероятности ошибки прогноза дает нормированную меру связи, известную как коэффициент Валлиса

Очевидно, что 0(X/Y)1, где (X/Y)=0 при статистической независимости и (X/Y)=1 при полной связи.

Данная мера связи также известна как коэффициент Гудмена-Крускала и является реализацией принципа пропорционального прогноза, высказанного Л.Гудманом и В.Крускалом. Согласно данному принципу, мера связи есть относительное уменьшение вероятности ошибки предсказания значений признака Х при знании значений признака Y по сравнению с вероятностью ошибки предсказания значений Х без Y. В соответствии с этим принципом по таблице сопряженности как бы предсказывается условная вероятность значений х_i, i=1,…r признака Х в доле случаев, соответствующих значению y_j признака Y. Если, например, (X/Y)=0,5, то это означает, что знание признака Y уменьшает число ошибок предсказания вдвое. Если (X/Y)=0.9, то это означает, что знание признака Y уменьшает число ошибок предсказания в 10 раз.

Построим здесь меру связи, которая может иметь ненулевое значение при статистической независимости признаков. Будем осуществлять прогноз значений признака Х на основе значений признака Y в таблице сопряженности. Очевидно, что наилучший прогноз возможен, когда некоторое значение y_j признака Y однозначно соответствует некоторому значению x_i признака Х, то есть p_i/j=P(X=x_i/Y=y_j)=1 при любых маргинальных распределениях X и Y. Будем полагать, что при наихудшем прогнозе некоторое значение y_j признака Y равномерно всем возможным значениям x_i, i=1,…r признака Х, то есть p_i/j=P(X=x_i/Y=y_j)=1/r. Тогда, даже при статистической зависимости признаков Х и Y, неравномерность маргинального распределения Х позволяет прогнозировать его значения по признаку Y. Определим нормированную меру прогноза как величину

где с- коэффициент нормировки, определяемый из условия (X/Y)=1 при максимальной связи.

Тогда получим

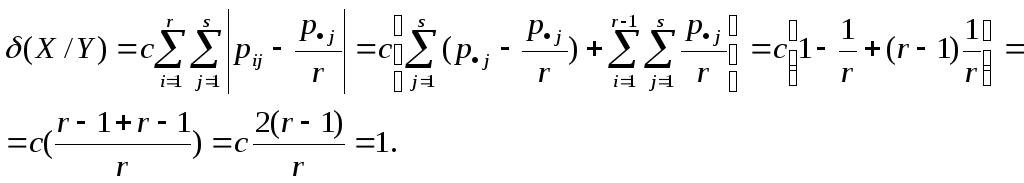
Отсюда получим и окончательно

Получим эквивалентное выражение для данной меры связи, в котором не требуется определять модуль разности для каждой ячейки таблицы сопряженности и суммируется меньшее число элементов, что может оказаться полезным при большем размере таблицы сопряженности. Пусть

и - множества индексовi значений x_i признака Х. Тогда получим