4.6. Восстановление функций степени достоверности.

Вновь обратимся к форме оптимального решающего правила и представим совместную плотность распределения p(_k,x) в виде p(_k,x)=f(x)p(_k|x). Заметим, что в таком выражении, которое является более традиционным в распознавании образов, оптимальное решающее правило непосредственно опирается на апостериорные вероятности появления классов или, другими совами, степени достоверности p(_k|x), k=1,,m. Такие функции, как правило, значительно проще плотностей распределения классов f(x|_k), так как функции степени достоверности отражают только взаимное различие плотностей распределения классов в основном лишь в небольших областях их перекрытия в признаковом пространстве. Взаимное различие плотностей распределения классов важно лишь в областях, где, по крайней мере, плотности двух классов _l и _к lk, отличны от нуля. В остальной же, большей части пространства, согласно гипотезе компактности, значения степени достоверности классов близки к 0 или 1. Очевидно, что в противном случае распознавание с приемлемо величиной риска ошибки просто невозможно. Поэтому обучение распознаванию строится как процесс непосредственного восстановления функций p(_k|x) ,k=1,,m без восстановления плотностей f(x|_k).

Пусть p(c|x) – некоторое параметрическое семейство действительны функций в пространстве признаков xRⁿ, удовлетворяющих условию 0p(c|x)1 для всех cR^p. Рассмотрим случайную величину

.

Если в данном параметрическом семействе p(c|x) существуют такие параметры c_k, к=1,,m, при которых апостериорные вероятности классов определяются через их значения p(c_k|)=p[g(}=_k|x()=] для всех Rⁿ, то в каждой точке признакового пространства условное математическое ожидание случайной величины z_k() совпадает с математическим ожиданием p(c_k|):

для всех Rⁿ.

Поэтому найдём коэффициенты с_к, к=1,,m из условий:

,

что означает

.

Если семейство функций p(c|x) регулярно, то получим критерий обучения

.

Пусть (x_i,g_i), i=1,,N – обучающая последовательность, на которой случайная переменная z_k() принимает значения

.

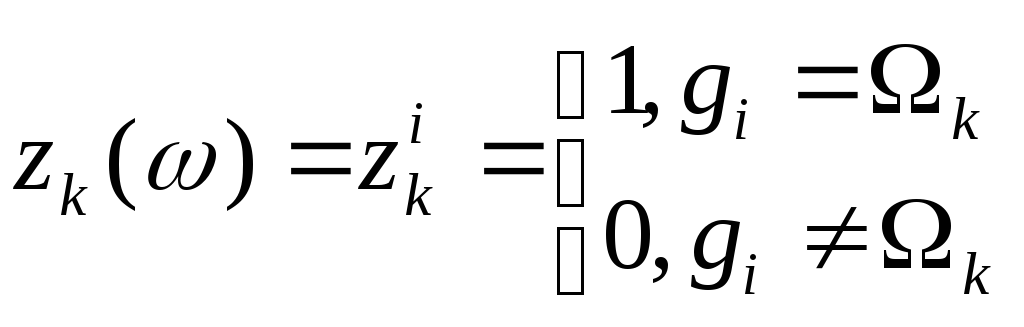Заменим операцию математического ожидания усреднением по выборке и получим

.

Отсюда получим итерационный градиентный алгоритм оценивания параметров

, s=1,,,

где _k^s – коэффициент основного шага в направлении антиградиента.

В случае бесконечной обучающей выборки (x_i,g_i), i=1,,, предъявляемой последовательно, рекуррентный алгоритм обучения строится как алгоритм стохастической аппроксимации Роббинса-Монро для решения уравнения регрессии

.

Рассмотрим систему некоторых функций y_i(x), i=1,,p, образующих пространство R^p, которое является спрямляющим для параметрического семейства p(c|x), таким, что

.

Тогда градиент grad_cp(c|x) определяется выражением

.

4.7. МИНИМИЗАЦИЯ СРЕДНЕГО РИСКА.

Методы оценивания плотностей распределения и функций степени достоверности восстанавливают полностью или частично вероятностные характеристики исходных данных. Лишь потом эти характеристики используются для формирования решающего правила. С другой стороны, можно строить алгоритмы обучения для непосредственного выбора решающего правила g(x), минимизирующего средний риск ошибки распознавания R[g()], не восстанавливая вероятностные характеристики исходных данных.

Рассмотрим некоторое заданное параметрическое семейство решающих правил и некоторую фиксированную функцию потерь [g(x),g()]. Тогда средний риск является функцией параметра с: R[g()]=R(c_=M{[g(x,c),g()]}. Тогда требование минимизации среднего риска приводит к условию равенства нулю его градиента.

grad_cR(c)=grad_cM{[g(x,c),g()]}=0.

Но для функции потерь вида [g(x),g()] перестановка операций дифференцирования и математического ожидания недопустима, так как выражение M{grad_c[g(x,c),g()]}0 (тождественно равно нулю) почти для всех с и изменяется скачком в зависимости от параметра с при любом х, так как g(x,c) зависит от с скачкообразно. Из-за этого рекуррентные градиентные процедуры типа стохастической аппроксимации здесь не используются.

Поэтому для построения процедуры обучения используют комбинацию дихотомических решающих правил вида

,

основанных, как правило, на линейной дискриминантной функции вида d(x,c)=c^Tx+c₀. Тогда параметрическая функция потерь определяется в виде

.

Такая функция штрафует не просто неправильное определение класса объекта, ни и слишком близкое расположение вектора х к разделяющей гиперплоскости в своём классе относительно порога  и, тем более, попадание вектора х в область чужого класса. Для такой функции потерь выражение для среднего риска R(с) уже обладает регулярностью, что приводит к невырожденному выражению регрессии

M{grad_c_kl[g(x,c),g()]}=0, k,l=1,,m.

Тогда в случае бесконечной обучающей выборки (x_i,g_i), i=1,,, предъявляемой последовательно, рекуррентный алгоритм обучения также строится как алгоритм стохастической аппроксимации Роббинса-Монро для решения уравнения регрессии

.

4.8. ЛИНЕЙНЫЕ РАЗДЕЛЯЮЩИЕ ФУНКЦИИ.

Как было показано, некоторое решающее правило g(x), независимо от способа его получения, определяет разбиение признакового пространства на области принятия решения ₁,,_m. Полагая, что решающее правило адекватно структуре обрабатываемых данных, мы считаем, что данные области принятия решений порождают разбиение всего множества исследуемы объектов Х на классы ₁,,_m. Тем самым мы полагаем, что посредством решающего правила g(x) строится отображение некоторого множества исходных образов, определённых на универсальном множестве , в признаковое пространство, представленное матрицей данных Х.

С другой стороны, решающее правило g(x) порождает совокупность границ, разделяющих области, соответствующие различным классам. Вид границ определяется решающим правилом, где, в частности, линейное решающее правило определяет линейные границы.

Для случая двух классов решающее правило определяет одну границу, такую, что решающее правило принимает совпадающее значение для объектов по одну сторону границы и несовпадающие значения для объектов по обе стороны границы. В таком случае решающее правило удобно определить в виде разделяющей функции вида

В случае линейной разделяющей функции получим .

Уравнение вида d(x,c)=0 определяет уравнение разделяющей гиперплоскости в признаковом пространстве. В двухмерном пространстве это просто прямая линия. Обозначив c=(c₁,,c_n)^T, получим уравнение гиперплоскости в виде d(x,c)=c^Tx+c₀=0. Отсюда получим c^Tx=-c₀, где c₀ – величина порога. Тогда

.

Возьмём две точки x₁ и x₂, принадлежащие разделяющей границе классов ₁ и ₂. Очевидно, что c^Tx₁+c₀=c^Tx₂+c₀, откуда c^T(x₁-x₂)=0. Следовательно, вектор с ортогонален вектору разности x₁-x₂. Так как вектор x₁-x₂ лежит в гиперплоскости, то вектор с определяет нормаль к ней и является её направляющим вектором, а коэффициент с₀ называется её смещением от начала координат (вдоль вектора с).

Рассмотрим геометрическое представление уравнения гиперплоскости в двухмерном пространстве (рис.4.2). очевидно, что для x₁-x₂ выполнены условия c^Tx₁=-c₀ и c^Tx₂=-c₀. Смещение с₀ определяется проекцией некоторого вектора, проведённого из начала координат, с концом, лежащим в гиперплоскости, на её направляющий вектор, например, c₀=-||x₁||||c||cos. В данном случае c₀>0. Тогда проекция некоторого произвольного вектора х на направляющий вектор гиперплоскости есть величина c_x=||x||||c||cos_x=c^Tx<0. Так как |c^Tx|<|c₀|, то d(x,c)=c^Tx+c₀=c_x+c₀>0 есть разность длин проекций или, другими словами, расстояние вектора х до гиперплоскости. Так как в данном случае d(x,c)>0, то нормальный вектор направлен в сторону области ₁, а расстояние до гиперплоскости в данной области положительно. В области ₂ расстояние до гиперплоскости считается отрицательным.

Следовательно, знак линейной разделяющей функции d(x,c) определяет принадлежность объекта х к одному из классов ₁ или ₂, а значение определяет расстояние до гиперплоскости при условии, что её направляющий вектор с имеет единичную длину. Если ||c||1, то расстояние от гиперплоскости до начала координат определяется величиной , а расстояние от некоторого вектора х до гиперплоскости определяется как величина .

Рис.4.2. Гиперплоскость и её направляющий вектор.

Для случая когда число классов m>2 удобно использовать различных решающих функций вида d_ij(x,c), где d_ij(x,c)=-d_ij(x,c). Например, для трёх классов нужно построить три гиперплоскости (рис. 4.3). Как видно, в данном случае имеется область неопределённого решения (ОНР), когда нельзя принять решение о классе объекта. Для такого объекта классификация не определена.

Рассмотрим расширенный вектор x=(x₁,,x_n,1)^T и вектор коэффициентов с=(с₁,,с_n,c₀) ^T. Тогда разделяющая функция имеет вид d(x,c)=c^Tx, а уравнение разделяющей гиперплоскости в новом, “расширенном” пространстве размерности n+1 имеет вид c^Tx=0. Согласно рассмотренному выше геометрическому представлению, всякая гиперплоскость c^Tx=0 имеет нулевое смещение, то есть проходит через начало координат в расширенном пространстве.

В расширенном пространстве удаётся, в частности, избежать появления областей неопределённости решений о классе (рис. 4.3). Например, в данном случае для трёх классов ОНР отсутствует в расширенном пространстве, которое полностью разбито на три области, каждая из которых содержит один класс.

Рис. 4.3.

1. Область неопределённого решения,

2. Отсутствие ОНР.

4.9. ОБЛАСТЬ РЕШЕНИЙ ЛИНЕЙНОЙ РАЗДЕЛЯЮЩЕЙ ФУНКЦИИ.

Рассмотрим снова случай двух классов. Пусть даны обучающие наблюдения (x_i,g_i), i=1,,N, g_i={₁,₂}. Мы хотим построить решающее правило распознавания g(x), ограничившись параметрическим семейством решающих правил вида g(x), ограничившись параметрическим решением решающих правил вида g(x,c) на основе построения линейной разделяющей функции вида d(x,c)=0. Предположим, что существует такая разделяющая функция , что вероятность неправильной классификации хотя бы одного наблюдения из обучающей выборки с её помощью очень мала. Если такую разделяющую функцию удаётся построить, то обучающую совокупность будем считать линейно разделимой. Естественно предположить, что в общем случае существует некоторое множество гиперплоскостей, разделяющих данную обучающую последовательность на два класса. Поэтому в общем случае существует вполне определённое множество направляющих векторов таких гиперплоскостей, образующих область решений в расширенном пространстве. (Рис. 4.4).

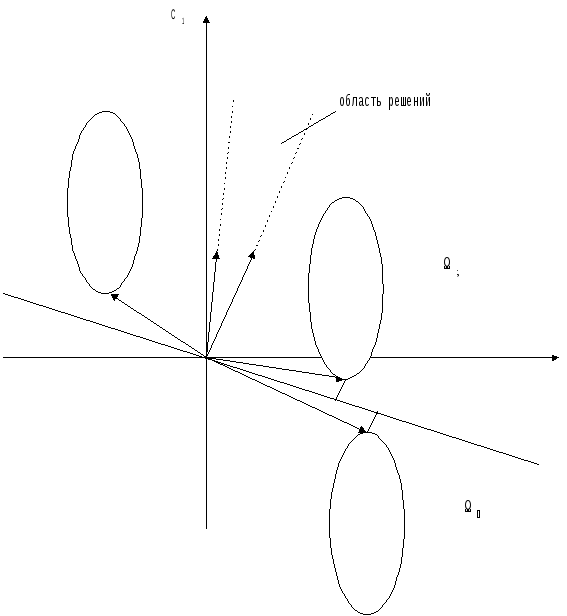
Рис. 4.4. Область решений для двух классов.

Очевидно, что множество направляющих векторов всех гиперплоскостей, разделяющих два класса, образуют конус в расширенном пространстве. Границами конуса являются направляющие векторы таких гиперплоскостей, которые сами проходят через некоторые граничные точки множества ₁и₂. Для направляющих векторовси области решений все объёкты обучающей совокупности классифицируются правильно, то есть выполнено:

,

где крайние положения при варьировании направляющего вектора определены моментом, когда в первый раз выполнились условия c^Tx=0, x₁иc^Tx=0, x₂для некоторых граничных точек₁ и₂.

Часто знак координат объектов из класса ₂инвертируют. Тогда все объекты обучающей совокупности₁₂^’ классифицируются правильно, еслиc^Tx>0, x₁₂^’, в крайние положения при варьировании направляющего вектора определяются выполнением условияc^Tx=0для некоторых граничных точек из₁₂^’.

Напомним некоторые определения. Пусть в n-мерном пространстве заданы два вектораx₁ иx₂. Тогда вектор разностиx₂-x₁направлен из точкиx₁ в точкуx₂, а векторx=x₁+(x₂-x₁)при 01лежит на отрезке, соединяющем точкиx₁ иx₂. Векторxназывается выпуклой линейной комбинацией точекx₁иx₂ и при варьированиипробегает все точки отрезка между точкамиx₁ иx₂.

Множество точек называется выпуклым, если любые его точки можно соединить отрезком, любая точка которого также принадлежит этому множеству.

Граничной точкой множества называется точка, в - окрестности которой при любомЮ0 содержатся точки, не принадлежащие данному множеству. В противном случае такая точка является внутренней точкой множества. Здесь- окрестностью некоторой точки а называется множество точекx, удовлетворяющих условию||x-a||<.

Множество называется замкнутым, если оно содержит все свои граничные точки.

Выпуклой оболочкой замкнутого выпуклого множества называется множество его граничных точек. Выпуклой оболочкой невыпуклого замкнутого множества называется множество граничных точек минимального выпуклого замкнутого множества, охватывающего данное.

Гиперплоскость называется опорной, если она проходит через некоторую граничную точку выпуклого замкнутого множества или, другими словами, касается его выпуклой оболочки.

Можно доказать, что, если выпуклые оболочки двух множеств не пересекаются и не соприкасаются, то их можно разделить более, чем одной гиперплоскостью, проходящей в расширенном пространстве через начало координат, множество направляющих векторов которых образуют выпуклый конус. Границы выпуклого конуса определяются направляющими векторами опорных гиперплоскостей, проходящих через начало координат.

Тогда в качестве разделяющей можно взять любую из гиперплоскостей, направляющий вектор которой лежит в области решений.

Но, как правило, из всего множества направляющих векторов в области решений стремятся выбрать один или хотя бы некоторое подмножество, являющихся в некотором смысле оптимальными по отношению ко всем векторам области решений.

Представление об оптимальности разделяющей гиперплоскости основано на том, что для разных разделяющих гиперплоскостей с направляющими векторами из области решений существуют в общем случае различные вероятности неправильной классификации. Поэтому оптимальная в некотором смысле гиперплоскость должна, в итоге, обеспечить уменьшение вероятности неправильной классификации.

Предположение о линейной разделимости обучающей совокупности на два класса ₁и₂при её неизвестных вероятностных характеристиках позволяет сформулировать понятие оптимальности разделяющей гиперплоскости непосредственно терминах гиперплоскостей, косвенно обеспечивая уменьшение вероятности ошибочной классификации.

Рассмотрим исходное (нерасширенное) пространство. Будем считать оптимальной гиперплоскость, которая наиболее удалена от выпуклых оболочек разделяемых множеств. (рис. 4.5).

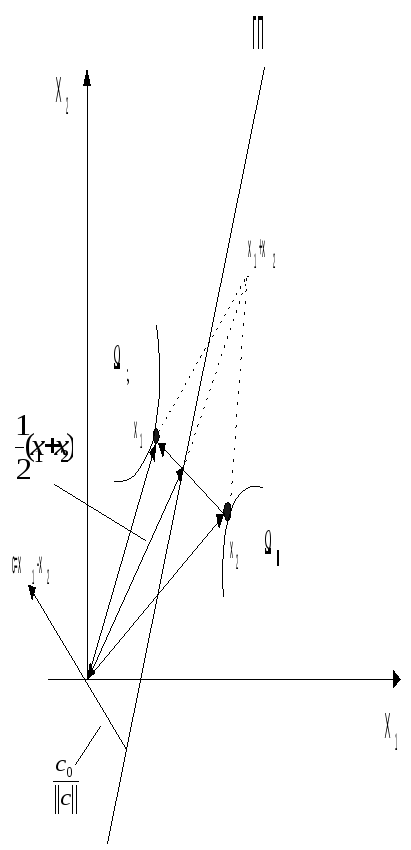
Рис. 4.5. Гиперплоскость, наиболее удалённая от выпуклых оболочек разделяемых множеств.

Пусть x₁₁иx₂₂– ближайшие точки выпуклых оболочек разделяемых множеств, где||x₁-x₂|| - минимальное расстояние среди всех точек выпуклых оболочек множеств₁и₂. Тогда оптимальная гиперплоскость определяется направляющим векторомc=x₁-x₂и смещением, проходя через середину отрезка, соединяющегоx₁₁ иx₂₂ перпендикулярно ему.

В другом случае (рис. 4.6) в расширенном пространстве оптимальные гиперплоскости не касаются выпуклых оболочек, а их направляющие векторы находятся внутри суженной области решений c^Tx>b, гдеb-некоторый допуск,x₁₂^’или

.

Рис. 4.6. Суженная область принятия решений.

С другой стороны, знание вероятностных характеристик обучающей совокупности позволяет оптимальное решающее правило в виде байесовского классификатора. Задавшись видом параметрического семейства распределений, мы тем самым можем определить параметры оптимальной разделяющей границы. Такую границу, как правило, можно определить как гиперплоскость в соответствующем спрямляющем пространстве.

Пусть, например, задано параметрическое нормальной семейство распределений. Пусть решающее правило

строится на основе разделяющей функции вида

d(x,c)=log p(x|₁)+log p(₁)-log p(x|₂)-log p(₂=0, где

p(x|_j)=N(_j,_j), j=1,2.

Тогда получим

D(x,₁,₁,₂,₂)=-(x-₁)^T₁^-1(x-₁)-log 2-log det₁+log p(₁)+

+(x-₂)^T₂^-1(x-₂)+ log2+log det₂-log p(₂).

Рассмотрим случай, когда ₁=₂=²E, где Е – единичная матрица. Такой случай возникает, когда признаки Х_j,j=1,,nстатистически независимы и имеют одинаковую дисперсию². Напомним, что такому случаю можно прийти, в частности, перейдя от стандартизованной матрицы данныхXк стандартизованной матрицеYпосредством ортогонального преобразованияY=ХАЛ^-0,5, где А – матрица собственных векторов корреляционной матрицы, а Л – диагональная матрица с собственными числами на главной диагонали. В этом случае₁=₂=Eи²=1, а классы₁и₂являются гиперсферами с центрами в точках₁и₂. Тогдаdet ₁=det₂=²ⁿ, ₁^-1=₂^-1=^-2E.

После преобразования и сокращения подобных получим разделяющую функцию

.

Если ²=1 иp(₁)=p(₂), то опустив, получим разделяющую функцию

D(x,₁,₂)=||x-₂||²-||x-₁||².

Решающее правило запишется как

.

Такое байесовское решающее правило часто называется классификатором по минимуму расстояния до эталона класса, где эталонами являются средние по классам ₁и₂.

С другой стороны

.

Данное уравнение определяет в исходном пространстве гиперплоскость с направляющим вектором ^-2(₁-₂) и смещением . Положив²=1 и р(₁)=P(₂) и введя обозначения c=(₁-₂) и c₀=(₁-₂)^T(₁+₂) получим уравнение оптимальной гиперплоскости, наиболее удалённой от гиперсферических оболочек классов ₁ и ₂ с радиусами гиперсфер r₁=r₂<|c₀|. Такая гиперплоскость проходит через середину отрезка перпендикулярно ему. Приp(₁)p(₂) гиперплоскость смещается в соответствующую сторону на величину log.

Рассмотрим другой простой случай, когда ковариационные матрицы классов совпадают ₁=₂=, а сами классы являются гиперэллипсоидами с центрами в точках ₁ и ₂ и полуосями, направленными вдоль собственных векторов ковариационной матрицы . Тогда дискриминантная функция имеет вид

d(x,₁,₂,)=[(x-₂)^T^-1(x-₂)-(x-₁)^T^-1(ч-₁)]+log.

В случае p(₁)=p(₂) байесовское решающее правило на основе такой дискриминантной функции называется классификатором по минимуму квадратичного махаланобисова расстояния до каждого из эталонов ₁ и ₂. Преобразуем выражение и получим

d(x,₁,₂,)=[x^T^-1x-2x^T^-1₂+₂^T^-1₂-x^T^-1x+2x^T^-1₁-₁^T^-1₁]+log=

=(₁-₂)^T^-1x-(₁-₂)^T^-1(₁+₂)+log=0.

Это уравнение гиперплоскости с направляющим вектором c^T=(₁-₂)^T^-1 и смещением -(₁-₂)^T^-1(₁+₂)+log. Так как направляющий вектор с в общем случае не совпадает с вектором ₁-₂, то разделяющая гиперплоскость в случае p(₁)=p(₂) проходит через середину ₁-₂ не ортогонально ему. Разделяющая гиперплоскость пройдёт через середину ₁-₂ ортогонально ему, если вектор ₁-₂ лежит в направлении некоторого собственного вектора матрицы ^-1, так как именно в этом случае выполнено (₁-₂)^T^-1=(₁-₂)^T, где  - является одним из собственных чисел _i, i=1,,n (рис. 4.7).

Рис. 4.7. Классификатор по минимуму махаланобисова расстояния.

4.10. АЛГОРИТМЫ ПОСТРОЕНИЯ РАЗДЕЛЯЮЩИХ ГИПЕРПЛОСКОСТЕЙ.

Алгоритмы такого типа возникают в детерминистской постановке задачи обучения распознаванию образов. Напомним, что в такой задаче, например для случая двух классов, предполагается, что плотности распределения вероятностей p(x|₁) и p(x|₂) сосредоточены целиком в непересекающихся областях пространства признаков ₁₂=. Условием успешного решения задачи обучения служит предположение о существовании в спрямляющем пространстве линейной дискриминантной функцией вида d(x,c)=0. Данная дискриминантная функция существует, если выпуклые оболочки разделяемых областей ₁ и ₂ не пересекаются. Тогда она выражается как линейная комбинация признаков с коэффициентами, значения которых определены направляющим вектором некоторой гиперплоскости, разделяющей области ₁ и ₂ в расширенном пространстве. Если выпуклые оболочки областей ₁ и ₂ соприкасаются, то разделяющая гиперплоскость является единственной. В противном случае множество таких гиперплоскостей. В качестве разделяющей принимается одна из них, либо произвольно, либо удовлетворяющая некоторому условию оптимальности. Следовательно, разделяющая гиперплоскость должна правильно классифицировать объекты x₁₂^’ обучающей совокупности, то есть вектор с должен удовлетворять системе линейных неравенств c^Tx>0, x₁₂^’, где ₂^’ является инверсией ₂.

Общий подход, используемый для нахождения решения такой системы линейных неравенств состоит в подборе некоторого критерия J(c), который минимизируется при условии, что вектор с является вектором решения. Тогда алгоритм строится как градиентная процедура поиска минимума критерия J(c).

Как известно, применение градиентных процедур сопряжено с целым рядом проблем. Содержательно, эти проблемы определяются сложностью формы поверхности, вид которой определён видом экстремизируемого функционала J(c): проблема начального решения, проблемы вычисления градиента, проблема выбора величины шага, проблема локальности решения, скорости сходимости и прочее.

Но в данном случае большинство данных проблем можно легко решить, так как мы можем сами определить вид функционала J(c), сделав его, естественно, как можно более простым. Наиболее естественно определить функционал J(c)как число неверно классифицированных объектов x₁₂^’. Очевидно, что данная функция критерия имеет единственный минимум, но вычисление её градиента вызовет трудности, так как она является кусочно-постоянной. Поэтому более удобной является другая простая функция, так называемая функция перцептрона, имеющая вид

, ₀₁₂^’, где ₀ – множество неверно классифицированных объектов обучающей совокупности.

Очевидно, что J_p(c)0 и достигает глобального минимума J_p(c)=0 когда множество неверно классифицированных объектов пусто. В этом случае вектор с принадлежит области решений линейной разделяющей функции d(x,c)=0. Геометрически функция J_p(c) пропорциональна сумме расстояний от неверно классифицированных объектов до разделяющей гипеплоскости. На рис. 4.8 показан её вид в двухмерном случае. Для расширенных векторов функция градиента имеет вид

, где ,i=1,,n, .

Пусть мы находимся на шаге sкорректировки вектора c_s. Получим его новое значение

,

где _s – длинна очередного шага. Следовательно, мы получили выражение для целого класса рекуррентных градиентных процедур минимизации функции перцептрона.

Рис. 4.8. Функции перцептрона.

Пусть снова (x_j,g_j), j=1,, - бесконечная обучающая последовательность. Тогда обобщенная итерационная процедура минимизации функции критерия для случая двух классов запишется как

c_j+1=c_j-_j_j_jgrad_cd(x_jmc_j), где

, ,

где _j – некоторая числовая последовательность, определяющая длину шага; коэффициент _j определяет, что изменение вектора с происходит лишь на тех шагах j, на которых очередной элемент (x_j,g_j) обучающей последовательности неверно классифицируется функцией d(xj_,c_j), то есть _jd(x_j,c_j)0;, коэффициент _j выполняет инверсию координат вектора x_j, если x_j₂, то есть _оx_j₂^’. Шаг длинны _о делается в направлении наибольшего возрастания функции _оd(x_обс_о)0.

Последовательность _j можно определить по-разному, например, _j=1 даёт правило постоянного приращения. Впервые оно было предложено Ф.Розенблаттом для перцептронной модели мозга как реализация принципа обучения с поощрением. В более общем случае _j0, например, _j=, образуя убывающую последовательность _j, где ,. Можно доказать, что число шагов_j=1 корректировки вектора с конечно. Для _j=1 этот факт известен как теорема о сходимости перцептрона.

Следовательно, дискриминантная функция d(x,c)=0 будет найдена с вероятностью 1 после конечного числа предъявлений объектов для распознавания. Алгоритмы такого вида называются конечно - сходящимися. Тем не менее, оценить, какая длина обучающей выборки является достаточной, в общем случае невозможно в принципе. Можно лишь оценить вероятность того, что дискриминантная функция уже обладает нужными свойствами на очередном шаге.

На практике длина обучающей совокупности конечна (x_j,g_j), j=1,,N. Поэтому дискриминантная функция строится путём многократного циклического предъявления объектов обучающей последовательности. Если дискриминантная функция d(x,c)=0 строится за конечное число шагов, то параметр с перестанет изменяться после конечного числа циклов обучения. Следует отметить, что обратное утверждение, вообще говоря, не верно. А именно, циклически сходящийся алгоритм обучения не обязательно окажется конечно - сходящимся, так как существует конечная вероятность того, что обучающая выборка конечного размера не является в достаточной степени представительной выборкой из генеральной совокупности.

4.11. АЛГОРИТМ ПОСТРОЕНИЯ ОПТИМАЛЬНОЙ РАЗДЕЛЯЮЩЕЙ ГИПЕРПЛОСКОСТИ.

Следует отметить, что требование линейной разделимости классов в детерминистской задаче распознавания является весьма жёстким априорным предположением о структуре данных. Легко предположить, что на практике это требование часто окажется невыполненным. Теорема о сходимости утверждает лишь то, что число корректировок решающего правила конечно в случае линейной разделимости данных и не определяет поведения конечно – сходящегося алгоритма в противном случае. На практике это означает, что без привлечения дополнительной информации, характеризующей поведение алгоритма, ничего нельзя сказать о том, зациклился алгоритм или длина обучающей выборки всё ещё недостаточно для его остановки.

Существуют различные способы эвристического усложнения общей градиентной процедуры построения разделяющей гиперплоскости, позволяющие предотвратить зацикливание. При остановке по признаку зацикливания либо отказываются от построения разделяющей гиперплоскости, либо определяют решение, оптимальное в некотором смысле по числу неверно классифицированных отчетов. В последнем случае естественно использовать детерминистские аналоги критериев оптимальности в вероятностной задаче обучения.

Рассмотрим итерационный алгоритм Б. Н. Козинца минимизации перцептронной функции критерия для случя двух классов, который находит оптимальную разделяющую гиперплоскость с направляющим вектором с и смещением с₀, либо устанавливает, что выпуклые оболочки разделяемых множеств пересекаются. Здесь, как было определено ранее, оптимальной называется гиперплоскость, наиболее удалённая от выпуклых оболочек разделяемых множеств.

Работу данного алгоритма удобно рассмотреть в исходном пространстве размерности n. Для различия множеств ₁и ₂сформируем дискриминантный функционал вида

, с=(с₁,,с_n)^T, x=(x₁,,x_n)^T.

Данный алгоритм за конечное число шагов находят точки x⁺₁ и x^–₂ выпуклых оболочек такие, что проекции отрезка между ближайшими точками выпуклsх оболочек на вектор x⁺-x^– меньше его длинны ||x⁺-x^–|| не более, чем на вершину ||x⁺-x^–||, где 0<<1 – достаточно малая наперёд заданная величина. В качестве разделяющей принимается гиперплоскость c^Tx+c₀=0 с направляющим вектором c=x⁺-x^– и смещением с₀=(x⁺-x^–)^T(x⁺-x^–), проходящая ортогонально через середину вектора x⁺-x^–. Если ||x⁺-x^–||<, где 0<<1 – достаточно малая наперйд заданная величина, то считается, что разделяющая гиперплоскость не существует.

Отметим важное свойство данного алгоритма. А именно, между гиперплоскостями, проходящими ортогонально через точки вектора x⁺-x^–, лежащие на расстоянии от его концов, гарантированно не содержится ни одной точки из множества ₁ и ₂. Такие гиперплоскости отличаются от оптимальной только своими смещениями

к множеству ₁ и

к множеству ₂ (рис. 4.9).

Рис. 4.9. Оптимальная разделяющая гиперплоскость.

Алгоритм работает следующим образом. Циклически поочерёдно просматриваются объекты из ₁₂, например в порядке следования в обучающей последовательности (x_k,g_k), k=1,,N. Если очередной объект x_k₁, то точка x_k^– остаётся без изменений x_k^–=x_k-1^–. Новая точка x_k^– определяется как точка вектора x_k-x_k-1⁺, ближайшая к точке x_k^–:

, ,

где

; .

Обозначим c_k-1=x_k-1⁺-x_k-1^– и получим

и .