
- •4. Проверка гипотезы по критерию х2.
- •5. Построение графика плотности и доверительных интервалов для параметров случайной величины.
- •Провести статистическую обработку результатов испытаний.
- •1. Построение гистограммы относительных частот.
- •4. Проверка гипотезы по критерию х2.
- •5. Построение графика плотности и доверительных интервалов для параметров m и .
МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО ОБРАЗОВАНИЯ РСФСР
ВСЕСОЮЗНЫЙ ЗАОЧНЫЙ МАШИНОСТРОИТЕЛЬНЫЙ ИНСТИТУТ
ВЫСШАЯ МАТЕМАТИКА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ ПО
МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ
Москва, 1987
АННОТАЦИЯ
Настоящее руководство является методическими указаниями по выполнению домашней контрольной работы по математической статистике. Указания содержат общую схему статистической обработки результатов наблюдений, подробнее описание реализации этой схемы и числовой пример.
Авторы: Виноградова К.С., Гильдерман И.Ю., Фокина Т.В.
Рецензент: доц. Кремлев В.Н.
Научный редактор: доц. Сорокина Е.М.
Рассмотрены и одобрены на заседании кафедры высшей математики 11 марта 1987г.
Рекомендуется к печати методической комиссией общетехнического факультета по результатам обсуждения на заседании методической комиссии23марта 1967г.,
протокол № 7
Председатель УМК: доц. Белов В. М.
Печатается по решению редакционно-издательского совета ВЗМИ от02.03.87 Тираж - 3000экз.
Председатель РИС: доц. Каниовский С.С.
Редактор РИО
Отдел стандартизации
Ответственный кафедры за выпуск учебно-методических материалов к.ф-м.н. Сорокина Е.М.
СХЕМА СТАТИСТИЧЕСКОЙОБРАБОТКИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ
Пусть в результате наблюдений получена некоторая выборка значений случайной величины Х: х1, х2, …, хn. Статистическую обработку этих опытных данных рекомендуется проводить по следующей схеме:
Построить гистограмму относительных частот
Построить группированный статистический рад.
Вычислить выборочную среднюю
 и
исправленную выборочную дисперсию S2
этого
ряда.
и
исправленную выборочную дисперсию S2
этого
ряда. Проверить по критерию х2 с уровнем значимости α= 0,05 непротиворечивость опытных данных гипотезе о нормальном распределении случайной величины с параметрами , S.
Если опытные данные не противоречат гипотезе о нормальном распределении:
а) построить на одном чертеже гистограмму относительных частот и график плотности нормального распределения с параметрами , S,
б)
с надежностью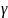 =
0,95 найти доверительные интервалы для
математического ожидания и среднего
квадратического отклонения исследуемой
случайной величины.
=
0,95 найти доверительные интервалы для
математического ожидания и среднего
квадратического отклонения исследуемой
случайной величины.
При выполнении контрольной работы рекомендуется пользоваться микрокалькулятором и числовыми таблицами. При этом промежуточные выкладки проводятся с точностью, которая обеспечивается микрокалькулятором и таблицам, а окончательные результаты округляются так, чтобы после запятой они содержали на один знак больше, чем исходные данные.
Литература
Чистяков В.П. “Курс теории вероятностей”. -2-еизд., М,:Наука, 1982.
Сборник задач по математике для втузов. Специальные курсы.
Гмурман В.Е. “Теория вероятностей и математическая статистика”. 5-е изд. М,,: Высшая школа, 1977.
РЕАЛИЗАЦИЯ СХЕМЫ
1. Построение гистограммы относительных частот.
На миллиметровой бумаге или обычной бумаге в клетку строим оси координат. Значения хi имеют определенный числовой разряд. Это единицы, десятки, сотни или, наоборот десятые, сотые и т.п. В зависимости от этого выбираем масштаб на оси Ох. Например, для выборки 130, 120, 180, 150 за единицу масштаба удобно взять десяток, а для выборки 0,15; 0,12; 0,14; 0,13 единицей масштаба может служить 0,01.
Находим наименьшей элемент выборки хmin и наибольший хmax. Исходя из характера выборки, задаем число a ≤ хmin, округляющее число хmin , или совпадающее с ним, и число h- длину интервала группировки. На оси Ох отмечает точки.
a0
=
a1,
a1=
a0
+h,
a2
=
a1
+
h
= a0
+2h,
… , =
a +
=
a +
 h
= b,
h
= b,
где натуральное число выбирается так, чтобы хmax<b. Таким образом, мы построим непересекающихся интервалов ∆i= [ai-1;ai), объединение которых, т.е. промежуток [a;b), содержит все элементы выборки. Число h выбирается из практических соображений, во всяком случае так, чтобы каждый интервал ∆i содержал элементы выборки, и промежуток [a;b) не слишком отличался от промежутка [хmin;хmax]. Как правило, число интервалов ∆i не меньше 6 и не больше 20.
По
оси Оу
будем
отмечать относительную частоту. Масштаб
на этой оси выбираем так, чтобы удобно
было отмечать величину C
=

Возвращаемся к выборке. Рассматриваем последовательно все её элементы, начиная с х1. Отыскиваем интервал [ai-1;ai),содержащий х1, и на высоте С над этим интервалом проводим черту. Также поступаем с х2, х3, ит.д. Если какой-то элемент попадает в интервал, над которым уже есть черта, проводим вторую черту на высоте С над первой. Если элемент попадает в интервал, над которым имеется две черты, проводим третью на высоте С над второй и т.д. до тех пор, пока ни дойдем до последнего элемента хn (рис. 1).

Рис. 1
Обозначим ni* число черточек над интервалом ∆i. Очевидно, это число элементов выборки, попавших в ∆i. Заменив каждый из этих элементов величиной хi*- серединой интервала ∆i, получим набор пар (хi*, ni*), i = 1, 2, …, , т.е. группированный статистический ряд, которым будем пользоваться в дальнейшем вместо исходной выборки.
Так
как высота столбика из черточек над
интервалом ∆i
равна
ni*C= ,
то
построенная на рис. 1 фигура является
гистограммой относительных частот.
,
то
построенная на рис. 1 фигура является
гистограммой относительных частот.
Подчеркнем ещё раз, что если элемент хi попадает на границу интервалов, мы относим его к правому интервалу.
2. Построение группированного статистического ряда.
Фактически, мы уже подучили группированный статистический ряд
(хi*,
ni*),
i
= 1, 2, …,
,
при построении гистограммы. Осталось
только записать
его
в
виде
таблицы. Для этого в первом столбце
таблицы
перечислим номера интервалов ∆i,
во втором столбце запишем координаты
хi*
середин
этих интервалов, а в третьем – количество
построенных черточек над интервалами
∆i
, т.е.
частоты ni*
(первые три столбца в таблице 1). Проверяем
выполнение равенства =n.
=n.
3. Вычисление выборочной средней и выборочной исправленной дисперсии S2.
Используя данные группированного статистического ряда, находим:
(1)

(2)

Таблица 1
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
№ |
хi* |
ni* |
ni* хi* |
|
|
|
|
f(zi) |
npi =
|
|
1 |
х1* |
n1* |
n1* х1* |
|
|
|
z1 |
f(z1) |
np1 |
|
2 |
х2* |
n2* |
n2* х2* |
|
|
|
z2 |
f(z2) |
np2 |
|
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
|
xr* |
nr* |
nr* хr* |
|
|
|
|
f( ) |
n |
|
|
|
|
|
|
|
|
|
|
|
|
Для удобства счета в четвертом столбце таблицы 1 записываем произведения ni* хi* , в последней ( +1)-ой строке этого столбца - вычисленное значение по формуле (1). В пятом столбце записываем | хi* - |, в шестом - квадрат этого модуля, в седьмой -
произведения
ni*(
хi*
-
)2,
в последней строке этого столбца -
вычисленное по формуле (2) значение S2
и .
.
4. Проверка гипотезы по критерию х2.
Значение статистики критерия х2 при данной выборке имеет вид:
(3)

где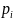 =
p(
x
=
p(
x ∆i)-
вероятность теоретического (предполагаемого
по гипотезе) распределения. В данной
задаче гипотеза состоит в том, что
теоретическое распределение нормально
с параметрами
, S.
∆i)-
вероятность теоретического (предполагаемого
по гипотезе) распределения. В данной
задаче гипотеза состоит в том, что
теоретическое распределение нормально
с параметрами
, S.
Поэтому
вероятность того, что значения случайной
величины x
попадают в интервал ∆i,т.е.
вероятность pi
,
можно приближенно вычислять по формуле
pi= f
(zi),где
f
(zi),где
 - значения нормированной величины.
- значения нормированной величины.
Чтобы
вычислить pi,
продолжим таблицу 1. Запишем в восьмом
столбце значения
 ,
используя для этого данные пятого
столбца и найденное значение S.
В девятом столбце запишем найденные
по таблице плотности f
(z)=
,
используя для этого данные пятого
столбца и найденное значение S.
В девятом столбце запишем найденные
по таблице плотности f
(z)=
 значения
f(
).
В
десятом столбце поместим значения npi
=
значения
f(
).
В
десятом столбце поместим значения npi
=
 .
Наконец, в одиннадцатом столбце запишем
значения дроби
и
в последней строке этого столбца -
значение
.
Наконец, в одиннадцатом столбце запишем
значения дроби
и
в последней строке этого столбца -
значение
 , вычисленное
по формуле (3).
, вычисленное
по формуле (3).
После
того как найденоtзначение
по таблице критических точек
распределения
 (
или по таблице квантилей
)
находим значение величины
(
или по таблице квантилей
)
находим значение величины
 (k),где
k
=
(k),где
k
=
 -
число степеней свободы,
- число интервалов группировки, a
-
число степеней свободы,
- число интервалов группировки, a -
принятый уровень значимости. В данной
задаче
= 0,05. Сравниваем
и
(k).
Если оказывается, что
-
принятый уровень значимости. В данной
задаче
= 0,05. Сравниваем
и
(k).
Если оказывается, что (k),
гипотезу о нормальном распределении
исследуемой величины x
отвергаем. В противном случае считаем,
что эта гипотеза не противоречит опытным
данным.
(k),
гипотезу о нормальном распределении
исследуемой величины x
отвергаем. В противном случае считаем,
что эта гипотеза не противоречит опытным
данным.
Замечание.
Необходимая точность метода обеспечивается
при условии, что во всех интервалах n 5. Если в каких-то интервалах указанное
условие не соблюдается, эти интервалы
надо объединить с соседними. В новых
интервалах, полученных объединением
ni*
и n
полагают равными суммам соответствующих
значений в объединяемых интервалах.
При этом получается новая группировка,
содержащая
5. Если в каких-то интервалах указанное
условие не соблюдается, эти интервалы
надо объединить с соседними. В новых
интервалах, полученных объединением
ni*
и n
полагают равными суммам соответствующих
значений в объединяемых интервалах.
При этом получается новая группировка,
содержащая интервалов. Значения n
новой
группировки записывают отдельно перед
итоговым столбцом.
интервалов. Значения n
новой
группировки записывают отдельно перед
итоговым столбцом.
5. Построение графика плотности и доверительных интервалов для параметров случайной величины.
Если гипотеза о нормальном распределении с параметрами , Sне отвергнута, полезно сравнить график плотности:
f(x)
=

и гистограмму относительных частот. Для этого на чертеже гистограммы относительных частот построим приближенно график плотности, найдя значения f (x) в пяти точках:
fmax
= f (
)=
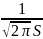 ;
;
f( S) =
S) =

(ординаты
точек перегиба) и f(
2S)
=

В
заключение находим доверительные
интервалы для математического ожидания
m
= M(m)
и среднего квадратического отклонения
 =
=
 .
Используем формулы:
.
Используем формулы:
(4)

(5)
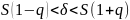
где
 и q
при заданной надежности γ = 0,95 находятся
по таблицам.
и q
при заданной надежности γ = 0,95 находятся
по таблицам.
Пример.
При расследовании причин аварии сварной конструкции было определено относительное удлинение металла 100 сварочных швов. При этом были получены следующие результаты (в процентах):
14,5 |
16,5 |
17,3 |
13,5 |
20,4 |
21,5 |
18,2 |
18,5 |
16,5 |
17,5 |
17,3 |
17,5 |
19,6 |
18,5 |
18,2 |
17,5 |
15,4 |
13,5 |
14,5 |
15,4 |
16,5 |
17,5 |
18,5 |
17,5 |
14,5 |
16,5 |
17,3 |
17,5 |
18,2 |
18,5 |
19,6 |
18,5 |
15,4 |
13,5 |
14,4 |
15,4 |
19,6 |
20,4 |
21,5 |
15,4 |
17,5 |
18,2 |
17,5 |
18,5 |
21,5 |
20,4 |
17,5 |
14,5 |
13,5 |
17,3 |
17,5 |
18,2 |
21,5 |
20,4 |
19,6 |
16,5 |
14,5 |
17,3 |
16,5 |
17,5 |
16,5 |
21,5 |
16,5 |
18,2 |
18,5 |
16,5 |
19,6 |
19,8 |
17,5 |
17,3 |
13,5 |
15,4 |
16,5 |
18,5 |
16,5 |
15,4 |
13,5 |
14,5 |
15,4 |
20,4 |
15,4 |
18,5 |
19,6 |
20,4 |
19,8 |
21,5 |
17,3 |
17,5 |
16,5 |
14,5 |
17,3 |
18,5 |
19,8 |
19,6 |
17,5 |
16,6 |
15,4 |
20,4 |
18,2 |
16,5 |


 2
2 )2
)2

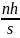 f(zi)
f(zi)

 2
2 )2
)2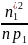
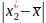
 2
2 )2
)2
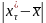
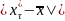 2
2 )2
)2




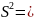

 .
.
