§ 52. Степенное множество графа

Степенным множеством графа называется множество степеней его вершин. От степенной последовательности о множество отличается тем, что в нем не учитывается число вершин, имеющих заданную степень, тогда как в степенной последовательности каждое число фигурирует столько раз, степенью скольких вер­шин оно является.

С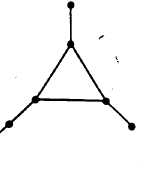 тепенное множество графа G обоз­начим через S(G). Так, для графа G, изображенного на рис. 52.1, S(G) = = {1, 2, 3}.

Хотя степенная последовательность графа удовлетворяет определенным условиям, однако степенным множеством графа может быть произвольное множество. Об этом свидетельствует следующая

Теорема 52.1. Любое конечное множество S натуральных чисел является степенным множеством некоторого порогового графа. Минимальный порядок таких графов равен s +1, где s — максимальное число из множества S. Очевидно, что из этой теоремы вытекает

Следствие 52.2. Любое конечное множество целых, неотрицательных чисел является степенным множеством некоторого графа.

Д оказательство теоремы 52.1. Если S(G) = = S, то \G\ ≥ s+ 1, так что нужно только доказать су­ществование подходящего графа G. Утверждение триви­ально для одноэлементного множества S, поскольку S(K_n)={n — 1}. Пусть теперь

и пусть, для определенности, п = 2р — четное число. Нуж­ный граф будем искать в виде

где К_Х°Н- граф, полученный из графа Н добавлением х доминирующих вершин, а О_У°Н — граф, полученный из графа Н добавлением у изолированных вершин. Лю­бой граф вида (1) является пороговым. Попытаемся по­добрать числа х_а и y_β в выражении (1) так, чтобы вы­полнялось - равенство S(G) = S. Для этого должно быть

О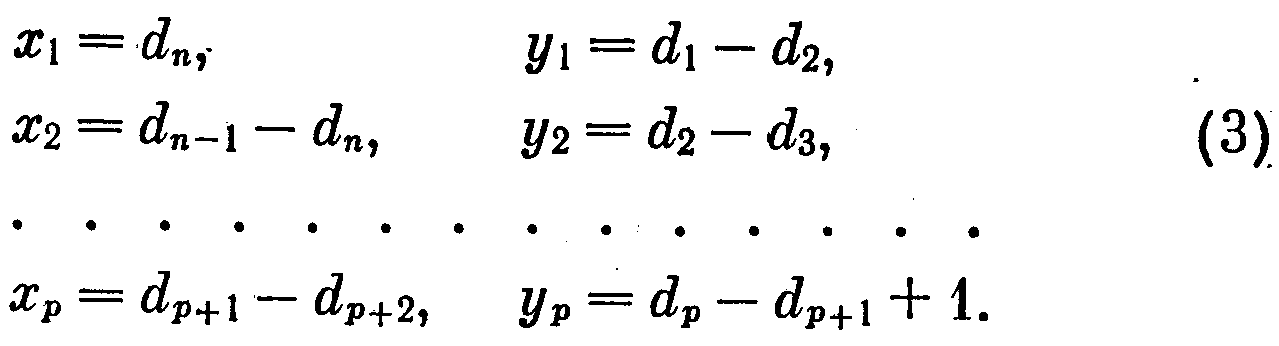 чевидно, что система уравнений (2) относительно не­известных х_i, yj (i =1,p,j =1, р) имеет решение, все координаты которого положительны:

Подставив в выражение (1) числа, определяемые равенст­вами (3), получим граф G, для которого S(G)=S. Число его вершин равно

Д ля нечетного п = 2р + 1 построение аналогично, толь-to вместо формулы (1) используется формула

Глава IX

Раскраски

§ 53. Правильная раскраска

Пусть G — некоторый граф, k — натуральное число. Произвольная функция вида

f:VG->{i, 2, ..., k} назы­вается вершинной k-раскраской, или просто k-раскраской, графа G. Если позволяет контекст, то k в этом определе­нии опускается. Раскраска называется правильной, если j(u) ≠ f(v) для любых смежных вершин и и v. Граф, для которого существует правильная k-раскраска, называется k-раскрашиваемым (или раскрашиваемым к цветами). В определении раскраски вместо множества {1, 2, ..., к} можно взять произвольное k-элементное множество.

П равильную k-раскраску графа можно трактовать как окрашивание каждой его вершины в один из k цветов, при этом смежные вершины должны получать различ­ные цвета. Поскольку функция ƒ не обязательно сюрьективна, то при k-раскраске фактически может быть ис­пользовано менее k цветов. Таким образом, правильную k-раскраску графа G можно рассматривать как разбие­ние

множества вершин VG на не более чем k непустых клас­сов, каждый из которых является независимым множест­вом. Классы этого разбиения называются цветными классами.

Минимальное число k, при котором граф G является k-раскрашиваемым, называется хроматическим числом этого графа и обозначается χ(G). Если χ(G) = k, то граф называется k-хроматическим. Правильная k-раскраска графа G при k = χ(G) называется минимальной.

В качестве иллюстрации рассмотрим граф G, изображеный на рис. 53.1, где указана одна из правильных раскрасок. Меньшим числом цветов этот граф раскрасить правильно нельзя. Действительно, граф содержит цикл (v₁ ,v₂ , v₃, v₄ , v₅ , v₁) для правильной раскраски которого нуж­но не менее трех цветов, а для вершины v ₆ требуется новый цвет. Итак, χ (G) = 4.

Р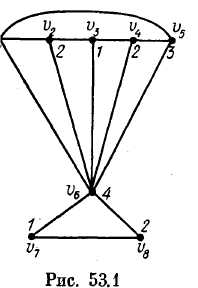 ассмотрим некоторые практи­ческие задачи, сводящиеся к пра­вильной раскраске графов.

1. Задача составления расписа­ний. Предположим, что нужно про­честь несколько лекций за крат­чайшее время. Чтение каждой лек­ции в отдельности занимает один час, но некоторые лекции не могут

читаться одновременно (например, их читает один и тотже лектор). Построим граф G, вершины которого би-тивно соответствуют лекциям, и две вершины смежны тогда и только тогда, когда соответствующие лекции нельзя читать одновременно. Очевидно, что любая правильная раскраска этого графа определяет допустимое расписание: лекции, соответствующие вершинам графа, составляющим етной класс, читаются одновременно. И, обратно, любое пустимое расписание определяет правильную раскраску графа G. Оптимальные расписания соответствуют минимальным раскраскам, а число часов, необходимое для проведения всех лекций, равно χ (G)

2. Задача распределения оборудования. Заданы множества V = {v₁ , v₂ , ..., v_n} и S = {s₁ , s₂ , ..., s_m} работ и механизмов соответственно. Для выполнения каждой из работ требуется некоторое время, одинаковое для всех работ, и некоторые механизмы. При этом никакой из механизмов не может быть одновременно занят в нескольких работах. Нужно распределить механизмы так, чтобы будущее время выполнения всех работ было минимальным. Построим граф G, положив VG = V и объявив вершины v_i и v_j (i ≠ j) смежными тогда и только тогда, когда для выполнения работ v_i и v_j , требуется хотя бы один общий механизм. При правильной раскраске графа G ра-тьт. соответствующие вершинам одного пвета. Можно выполнять одновременно, а наименьшее время выполне­ния всех работ достигается при минимальной раскраске.

3. Задача о проектировании коробки скоростей. Короб­ка скоростей — механизм для изменения частоты враще­ния ведомого вала при постоянной частоте вращения ве­дущего. Это изменение происходит за счет того, что на­ходящиеся внутри коробки шестерни (зубчатые колеса) вводятся в зацепление специальным образом. Одна из задач, стоящая перед конструктором коробки, заключает­ся в минимизации ее размеров, а это часто сводится к минимизации числа валов, на которых размещаются шестерни.

Построим граф G, вершины которого биективно соот­ветствуют шестерням. Если по какой-то причине две шестерни не должны находиться на одном валу (напри­мер, они могут быть в зацеплении, или их общий вес велик для одного вала и т. д.), то соответствующие вер­шины графа соединим ребром. Вершины, имеющие один цвет при правильной раскраске этого графа, определяют шестерни, которые могут находиться на одном валу, а хроматическое число χ (G) равно минимальному коли­честву валов, нужных для проектируемой коробки.

Для некоторых графов, хроматические числа найти не­сложно. Например, χ (К_п) = п, χ (К_п — е) = п—1, χ (K_n,m) =2, χ (С_2п+1) = 2, χ (С_2n+1) = 3.

Очевидно, что граф является 1-хроматическим тогда и только тогда, когда он пустой, а 2-хроматическим — когда он двудольный и непустой. Обычно 2-хроматический граф называют бихроматическим. Поэтому теорему Кёнига о двудольных графах можно сформулировать в следующем виде:

Теорема 53.1. Непустой граф является бихромати­ческим тогда и только тогда, когда он не содержит цик­лов нечетной длины.

Задачи определения хроматического числа и построе­ния минимальной раскраски произвольного графа явля­ются очень сложными, эффективные алгоритмы их ре­шения неизвестны. Рассмотрим простой алгоритм построе­ния правильной раскраски, в ряде случаев приводящий к раскраскам, близким к минимальным.

Алгоритм последовательной раскраски.

1. Произвольной вершине v₁ графа G припишем цвет 1.

2. Если вершины v₁ , v₂ , ..., v_i раскрашены l цветами 1, 2, ..., l, l ≤ i, то новой произвольно взятой вершине v_i+1 припишем минимальный цвет, не использованный при раскраске вершин из ее окружения.

Раскраека, к которой приводит описанный алгоритм, называется пдследовательной. Очевидно, что это — пра­вильная раскраска. Для некоторых классов графов (на­пример, полных однодольных) последовательная раскраска является минимальной. В общем случае это не так.

Следующая теорема сводит задачу построения пра­вильной раскраски графов к аналогичной задаче для двухсвязных графов.

Теорема 53.2. Если каждый блок графа к-раскрашиваем, то и сам граф также к-раскрашиваем.

Воспользуемся индукцией по числу блоков рассмат­риваемого графа. Для графа, являющегося блоком, ут­верждение тривиально. Предположим, что теорема верна для графов, состоящих из m ≥ 1 блоков. Пусть теперь G — граф, имеющий ровно m + 1 блоков, В — один из его концевых блоков, Н — объединение всех остальных бло­ков. По индуктивному предположению оба графа В и Н являются k-раскрашиваемыми. Зафиксируем для каждого из них правильную k-раскраску.

Графы В и Н имеют ровно одну общую вершину v. Если ее цвета в обеих фиксированных k-раскрасках сов­падают, то получена правильная k-раскраска графа G. В противном случае нужно очевидным образом переста­вить цвета в одной из фиксированных раскрасок.