1.7 Расчет площади треугольника

Площадь треугольника определим методом численного интегрирования. Рассмотрим рис. 4а. Как видно, площадь треугольника можно определить как сумму площадей, расположенных под сторонами АВ и АС минус площадь, расположенную под стороной АС. Для треугольника с рис. 4 б) площадь определяется как площадь под стороной АВ минус сумма площадей под сторонами АС и ВС. К каждой из фигур, составляющих треугольник можно применить один из методов численного интегрирования, т.к. сверху эти фигуры ограничены некоторой функцией (в нашем случае это уравнение прямой) слева и справа - прямыми, параллельными оси OY.

Рис. 4. Определение площади треугольника

Запишем уравнение прямой:

y = kx + b

Для каждой пары точек определяющих сторону треугольника составляется уравнение прямой, т.е. рассчитываются коэффициенты k и b:

После этого составляется уравнение прямой и определяется площадь под этой прямой. Это производится для всех сторон, составляющих треугольник. Вначале производится суммирование площадей - движение по верхней части треугольника, при переходе на нижнюю часть, найденные площади вычитаются из общей площади.

1.8 Расчет радиуса вписанной окружности

Радиус вписанной окружности определяем из соотношения:

S - площадь треугольника;

P - полупериметр.

Длины двух сторон нам известны, длина третьей стороны определяется как

.

1.9 Определение координат центра вписанной окружности

Как известно, центр вписанной окружности лежит на пересечении биссектрис треугольника (рис. 5). Для нахождения точки пересечения необходимо составить уравнения прямых для двух любых биссектрис и найти их общее решение.

Для составления уравнений биссектрис необходимо:

- провести из вершины А дугу произвольного радиуса (чтобы точки пересечения окружности со сторонами лежали внутри треугольника, рис. 6а).

- используя уравнение окружности и прямой найти точки пересечения дуги с двумя сторонами треугольника, выходящими из рассматриваемой вершины АС и АВ.

- соединить точки пересечения и рассмотреть полученный равнобедренный треугольник АDE (рис. 6б).

- найти середину стороны DЕ.

- найти коэффициенты прямой, проходящей через точки В1 и А.

Рис. 5. Определение центра вписанной окружности

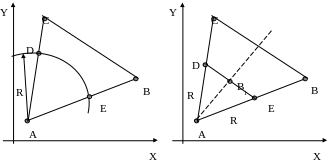
а) б)

Рис. 6. Построение биссектрисы

Рассматривая другую вершину (например А или С), находим коэффициенты второй биссектрисы.

После того, как найдены коэффициенты биссектрис, определяем точку их пересечения.

Точки пересечения окружности и прямой будем находить используя метод бисекций.

Рассматриваем произвольную вершину треугольника. Из нее, как из центра, проводим окружность произвольного радиуса и определяем точку пересечения окружности со сторонами, принадлежащими вершине:

- определяем коэффициенты уравнения прямой для стороны:

B₁=Y₁-K₁X₁

- задаем интервал нахождения пересечения A, B;

- находим середину ;

- подставляем х в уравнение прямой

y₁ = K₁x+B₁

и окружности с центром в точке Cx, Cy

Если |y₁ – y₂| меньше заданной точности е, то расчет считаем законченным. Иначе сравниваем значения y₁ и y₂ и, если y₁ > y₂, присваиваем

A = x

а если y₂ > y₁, то

В = х

и вновь повторяем расчет.

После этого аналогично находим точку пересечения окружности с другой стороной, принадлежащей рассматриваемой вершине.

Координаты середины

Определяем коэффициенты биссектрисы:

B₁=Yс – K₁Xс

Проводя аналогичные вычисления находим коэффициенты прямой для второй биссектрисы К₂, В₂.

Далее методом бисекций определяем точку пересечения биссектрис по алгоритму, описанному в разделе 1.6 и в результате получим координаты центра вписанной окружности.