
- •1.Взаємо-однозначна відповідність. Еквів. Множин.
- •2. Потужність множин. Порівняння потужностей.
- •3. Теорема Кантора-Бернштейна.
- •4. Поняття зчисленної множини. Найпростіші властивості.
- •5. Об'єднання зчисленної кількості зчисленних множин
- •6. Зчисленність множин цілих, раціональних чисел.
- •7. Алгебраїчні числа. Зчисленність мн-ни алг. Чисел.
- •8. Незчисленність чисел відрізку [0;1]
- •10. Підмножини даної множини. Існування потужності, вищої від даної.
- •11. Граничні точки множини. Замкнені множини, властивості замкнених множин.
- •12. Внутрішні точки множини. Відкриті множини. Властивості відкритих множин.
- •13. Критерій відкритої підмножини дійсних чисел
- •14. Критерій замкненої підмножини дійсних чисел.
- •15. Побудова канторової множини дійсних чисел
- •16. Властивість касторової множини(непорожність, замкненість, потужність множини кінців суміжніх інтервалів.)
- •17.Потужність точок канторової множини
- •18.Зовнішня міра Лебега лінійної множини.
- •19. Приклади скінченних, зчисленних множин та їх міри Лебега.
- •21. Вимірність обмеженої відкритої множини
- •22. Вимірність обмеженої замкненої множини
- •23. Вимірність канторової множини, її міра Лебега
- •24. Вимірні функції
- •25. Властивості вимірних функцій: вимірність суми, різниці, добутку та частки вимірних функцій.
- •26. Інтеграл Рімана. Критерій інтегрованості функції за Ріманом.
- •26. Інтеграл Рімана. Критерій інтегрованості функції за Ріманом.
- •27. Прості функції, інтеграл Лебега від простої функції.
- •28. Інтеграл Лебега, його найпростіші властивості
- •20.Властивості міри Лебега.
- •9.Множини потужності континуум та їх властивості.Потужність множини дійсни числ.
- •29. Рівність функцій майже всюди та інтеграл Лебега.
- •30. Зв'язок інтеграла Рімана та інтеграла Лебега. Інтеграл Рімана .
- •31. Граничний перехід під знаком інтегралу Лебега
- •33. Нерівність Чебишева
- •34. Наслідок з нерівності чебишева. Простори
- •35. Звязок інтегралів Рімана та Лебега
30. Зв'язок інтеграла Рімана та інтеграла Лебега. Інтеграл Рімана .
Інтеграл
Рімана
 . Цей
інтеграл
не належить від способу вибору відмічених
точок
. Цей
інтеграл
не належить від способу вибору відмічених
точок
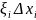 .
Вводиться
для обмеженої на [a; b] f(x) cуми Дарбу
.
Вводиться
для обмеженої на [a; b] f(x) cуми Дарбу
 ,
де
,
де
 .
.
 ,де
,де

Теорема.(критерій інтегрованості f(x)): інтеграл Рімана від обмеженої f(x) на [a; b]

Теорема 1(критерій інтегрованості за Ріманом): інтеграл Рімана від обмеженої f(x) на [a; b] ∃⇔ міра Лебега всіх точок розриву f(x) на [a; b] рівна 0.
Випадки:1)
f(x) неперервна на [a; b], тоді точок розриву
на [a; b] не буде
 інтегрована за Ріманом на [a; b]. 2)
f(x)
на [a; b] має скінчену кільк. точок розриву
інтегрована за Ріманом на [a; b]. 2)
f(x)
на [a; b] має скінчену кільк. точок розриву
 ,
тоді
,
тоді
 кусково неперервна f(x)
інтегрована за Ріманом на [a; b]. 3)
функція Діріхле D(x)=
кусково неперервна f(x)
інтегрована за Ріманом на [a; b]. 3)
функція Діріхле D(x)= . Якщо
. Якщо
 -
деяка точка, то в
її околі буде безліч рац. точок, так і
іррац. А) візьмемо послідов.
-
деяка точка, то в
її околі буде безліч рац. точок, так і
іррац. А) візьмемо послідов.
 ,
і
,
і
 - рац.
точки .
- рац.
точки .
Тоді
D(x)=0 .
Б)
.
Б)
 ,
,
 і
і

 -іррац.
точки . Тоді D(x)=1
-іррац.
точки . Тоді D(x)=1 .
Точки розриву функцій Діріхле – це всі
точки числової прямої. Якщо розглядати
.
Точки розриву функцій Діріхле – це всі
точки числової прямої. Якщо розглядати
 , то
, то
 .
Тоді
.
Тоді
 ,
,
Теорема.
Якщо ф-я f(x)
обмежена на [a; b] і
інтеграл Рімана
 , то тоді
інтеграл Лебега [a;b]
, то тоді
інтеграл Лебега [a;b]
 .
.
31. Граничний перехід під знаком інтегралу Лебега
Теорема
(Лебега
про граничний
перехід під знаком
 -інтеграла).
Нехай
-інтеграла).
Нехай
 ,
причому
,
причому
 -скрізь
на E. Тоді
-скрізь
на E. Тоді
 ,
,
 0
0
 і, якщо p = 1 або
і, якщо p = 1 або
 ,
то
,
то

Зауваження.
Нерівність
 можна вимагати
|
|-
скрізь на
E.
можна вимагати
|
|-
скрізь на
E.
Розглянемо
тепер послідовність ( )
функцій
)
функцій
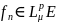 ,
яка збігається
,
яка збігається – скрізь на Е до функції
,
причому
– скрізь на Е до функції
,
причому
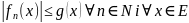 ,
а функція
,
а функція
 .
Вирішимо питання про
.
Вирішимо питання про
 – інтегрованість функції
і відповідну рівність
– інтегрованість функції
і відповідну рівність
 .
.
Спочатку
вважаємо, що
 .
Тоді можна утворити
.
Тоді можна утворити
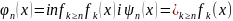 .
Зрозуміло, що
.
Зрозуміло, що

утворимо також функції

які задовольняють нерівності

І тому
 З іншого
боку,
З іншого
боку,

За
наслідком кожна функція
 Тому за теоремою Бенно Леві
Тому за теоремою Бенно Леві
 .
Звідси, враховуючи нерівності
.
Звідси, враховуючи нерівності

та умову,
що
 – скрізь на Е, знову за теоремою Бенно
Леві дістаємо, що
і, коли додатково p=1
або
,
то
– скрізь на Е, знову за теоремою Бенно
Леві дістаємо, що
і, коли додатково p=1
або
,
то

Аналогічно
доводимо, що
 .
Тому з нерівностей
.
Тому з нерівностей
 за властивістю монотонності
–інтеграла
дістаємо, що
за властивістю монотонності
–інтеграла
дістаємо, що
 ,
коли p=1
або |μ|(E)<+∞.
,
коли p=1
або |μ|(E)<+∞.
Нехай
тепер
 ,
де Ф – довільний бананів простір. Тоді
,
де Ф – довільний бананів простір. Тоді
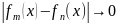 , коли m
і n
, коли m
і n
 –скрізь
на Е, оскільки
–скрізь
на Е, оскільки
 і
і
 –скрізь
на Е. Крім того,
–скрізь
на Е. Крім того,
 .
Тому за доведенням для будь-яких
послідовностей
.
Тому за доведенням для будь-яких
послідовностей
 і
і
 .
.
Звідси
випливає, що
 ,
коли m
і n
,
тобто послідовність
,
коли m
і n
,
тобто послідовність
 фундаментальна у просторі
фундаментальна у просторі
 .
Тепер, як і при доведенні теореми Бенно
Леві, доводимо, що
і, коли p=1
або
.
Тепер, як і при доведенні теореми Бенно
Леві, доводимо, що
і, коли p=1
або
 ,
то
,
то

32. Теореми Б.Леві та Фату


33. Нерівність Чебишева
Якщо
 на мн. А і
на мн. А і ,
то тоді
,
то тоді

Дов.
 ,
тоді
,
тоді
.
 і ці ддві множини не перетинаються
і ці ддві множини не перетинаються

Ділисо
на с ,маємо
,маємо
 .
.
34. Наслідок з нерівності чебишева. Простори
Якщо
 ,
то тоді f(x)=0
майже всюди на множині А.
,
то тоді f(x)=0
майже всюди на множині А.
Дов.
 і с=
і с= ,
,

 для всіх
для всіх
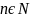
Остаточно

Зауваження.
 – множина всіх
f(x)
для яких існує
– множина всіх
f(x)
для яких існує

А)
 для всіх f
є
для всіх f
є ,
при чому
,
при чому
 f=0.
f=0.
Простори
 і т. п. з інтегралом Лебега при переверці
1-ї аксіоми норми
і т. п. з інтегралом Лебега при переверці
1-ї аксіоми норми

 на
А т. т
на
А т. т

Наслідок
2. Якщо

Дов.
 аналогічне доведення
аналогічне доведення

Зауваження.


