2. Нахождение оптимального опорного плана. Переход к нехудшему опорному плану

Пусть дана ЗЛП, записанная в канонической форме:

;

,

,

Для нахождения начального опорного плана также составляется жорданова таблица, но несколько в ином виде.

Таблица 2.2.

.

Такую таблицу еще иначе называют симплексной (или симплекс-таблицей).

Симплексную таблицу преобразовываем шагами жордановых исключений, замещая нули в левом крайнем столбце соответствующими . При этом на каждом шаге разрешающим может быть выбран любой столбец, содержащий хотя бы один положительный элемент. Строка целевой функции на выбор разрешающих столбцов на данном этапе никакого влияния не оказывает. Разрешающая строка определяется по наименьшему из отношений свободных членов к соответствующим положительным элементам разрешающего столбца.

Если в процессе исключений встретится 0-строка, все элементы которой равны нулю, а свободный член отличен от нуля, то система ограничений уравнений решений не имеет. Если же встретится 0-строка, в которой, кроме свободного члена, других положительных элементов нет, то система ограничений уравнений не имеет неотрицательных решений.

Итак, через некоторое число шагов жордановых исключений приходим к следующей симплекс-таблице.

Таблица 2.3.

.

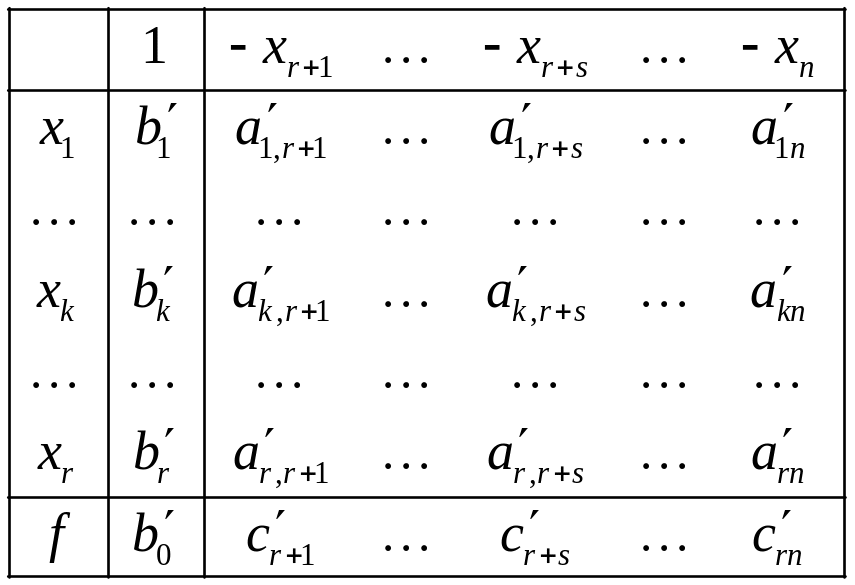Из этой симплексной таблицы находим начальный опорный план

,

где переменные  базисные, а переменные  свободные.

После нахождения начального опорного плана возникает вопрос: достигает ли целевая функция максимального значения при полученном начальном опорном плане, или следует находить новые опорные планы с большим значением .

В качестве ответа на этот вопрос рассмотрим следующие теоремы (без доказательства).

Теорема 2.6. Если в симплекс-таблицы задачи на максимум, содержащей некоторый опорный план , все элементы -строки (кроме ) неотрицательны ( ), то  оптимальный план и на многограннике допустимых планов.

Теорема 2.7. Если в -строке нет нулевых элементов, то оптимальный план единственный.

Если в -строке среди элементов есть хотя бы один нулевой (кроме ), то оптимальных планов бесконечное множество.

Теорема 2.8. Если в -строке есть хотя бы один отрицательный элемент (кроме ), а в соответствующем ему столбце нет положительных элементов, то целевая функция не ограничена в допустимой области. ЗЛП не имеет решения.

Теорема 2.9. Если в симплекс-таблице, содержащей некоторый опорный план , в -строке есть хотя бы один отрицательный элемент (кроме ), а в каждом столбце с таким элементом есть хотя бы один положительный элемент, то можно перейти к новому опорному плану , более близкому к оптимальному, т.е. .

Переход к нехудшему опорному плану

1) Столбец с отрицательным элементом в -строке берут за разрешающий. Если в -строке отрицательных элементов несколько, то за разрешающий выбирают столбец с наибольшим по абсолютной величине отрицательным элементом в -строке.

2) Определяют по минимальному симплексному отношению разрешающую строку и делают шаг жорданова исключения см. стр. 29.

3) Полученный опорный план вновь исследуют на оптимальность.

Описанный процесс повторяется до тех пор, пока не будет найден оптимальный опорный план, либо установлена неразрешимость задачи.

Задачу минимизации можно формально заменить задачей максимизацией функции , так как .

Пример 2.10. Найти оптимальный опорный план ЗЛП, используя симплекс-метод

;

.

Решение. Задача записана в канонической форме, но два свободных члена в системе ограничений отрицательны, поэтому умножаем первое и второе уравнения на . Получаем

Целевую функцию и систему ограничений-равенств можно записать в виде:

;

Сразу выделить базисные переменные мы не можем, поэтому находим начальный опорный план, построив симплекс-таблицу.

.

За разрешающий столбец можно взять столбец , т.к. элемент в -строке отрицательный, или любой из столбцов , , .

Возьмем столбец . Разрешающим будет элемент 2, стоящий в третьей сроке, так как он в этом столбце единственный положительный элемент. Делаем шаг жордановых исключений. Переменная идет в базисные. Элементы третьей строки делим на разрешающий элемент. А остальные элементы таблицы, в том числе и -строки, находятся по формуле , , где элемент  разрешающий,  элемент, стоящий в разрешающей строке и -том столбце,  элемент, стоящий в разрешающем столбце и -ой строке,  элемент, стоящий в -ой строке и -том столбце.

Получаем следующую симплекс-таблицу

.

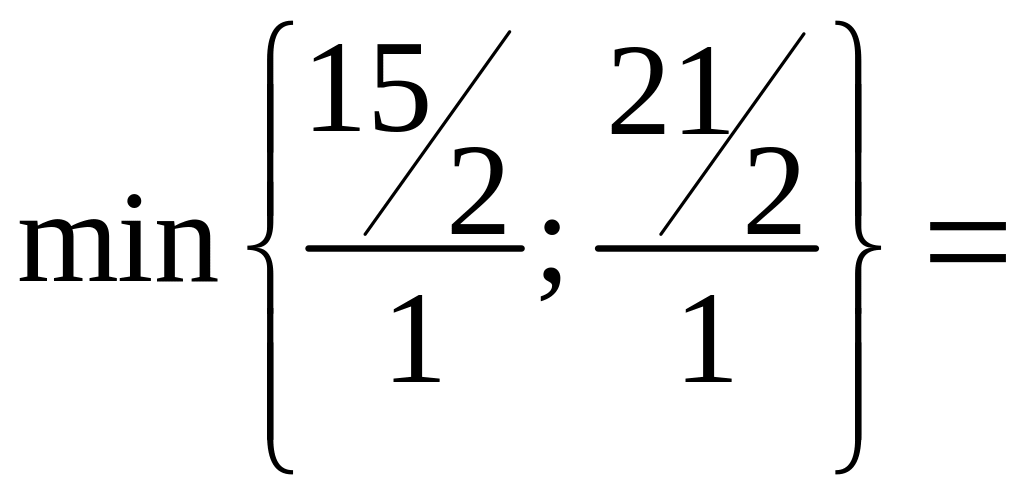
За разрешающий столбец возьмем , так как в нем есть положительные элементы. Разрешающую строку определим из отношений: . Значит, элемент 1, стоящий в первой строке будет разрешающим. Делаем шаг жордановых исключений и получаем следующую симплекс-таблицу

.

Теперь за разрешающий столбец возьмем с разрешающим элементом 3, которой находится во второй строке. Делаем шаг жордановых исключений и получаем следующую симплекс-таблицу

.

В результате получаем опорный план , значение целевой функции при этом .

Так как в -строке не отрицательных элементов, то выполняется условие оптимальности.

Таким образом, оптимальный опорный план , .

Ответ: , .



Пример 2.11. На предприятии имеется возможность выпускать три вида продукции П₁, П₂ и П₃. При ее изготовлении используются ресурсы Р₁, Р₂ и Р₃. Размеры допустимых затрат ресурсов ограничены соответственно величинами , и . Расход ресурса -го ( ) вида на единицу продукции -го ( ), а также цена единицы продукции -го вида (ден. ед.) даны в таблицы.

Ресурсы	Продукция			Объем ресурсов
	П1	П2	П3
Р1 Р2 Р3	0 2 1	2 4 0	5 2 1	5 4 2
Цена единицы продукции, ден. ед.	20	8	30

1) Построить экономико-математическую модель задачи.

2) Симплексным методом найти план выпуска продукции по видам с учетом имеющихся ограниченных ресурсов, который обеспечивал бы предприятию максимальный доход.

Решение. 1) Пусть – объем выпускаемой продукции вида П₁; – объем выпускаемой продукции вида П₂; – объем выпускаемой продукции вида П₃. Тогда – план выпуска продукции. Прибыль, которую получит предприятие при продаже всей продукции, составит ден.ед. Естественно, предприятие стремится максимизировать эту прибыль, поэтому целевая функция принимает вид .

На производство всех видов продукции будет затрачено единиц ресурсов P₁; единиц ресурсов P₂ и единиц ресурсов P₃. Предприятие может использовать как все ресурсы в полном объеме, так и меньшее их количество. По смыслу задачи все переменные .

Таким образом, получаем следующую математическую модель данной задачи:

;

.

2) Построенная математическая модель задачи является задачей линейного программирования, для решения которой используем симплекс-метод.

Предварительно приводим задачу к канонической форме записи. Для этого в ограничения-неравенства вводим неотрицательные балансовые переменные , и . Получаем

;

.

Этой задаче соответствует следующая симплекс-таблица (сразу разрешенная относительно переменных , и ).

.

В -строке определяем максимальный по модулю отрицательный элемент: . Значит, столбец с переменной будет разрешающим. Для определения переменной, выводимой из базиса, находим симплексные отношения по следующей формуле: 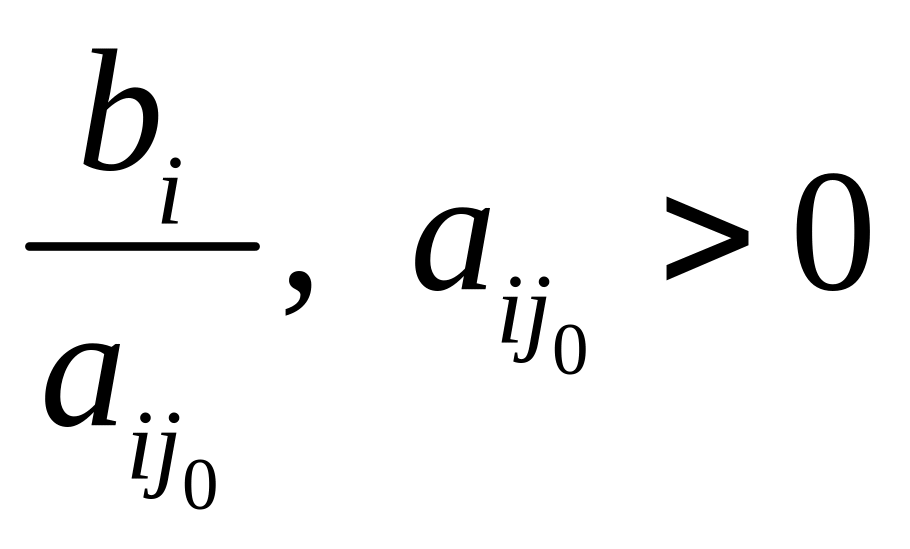. Среди симплексных отношений определяем наименьшее: .

Значит, элемент – разрешающий элемент. Из базисных исключаем переменную и вносим переменную . Преобразовываем таблицу по правилу ПОЗ: а) разрешающий элемент заменяется обратным; б) остальные элементы разрешающей строки делятся на разрешающий элемент, т.е. на ; в) элементы разрешающего столбца делятся на разрешающий элемент и меняют знак на противоположный; г) прочие элементы таблицы вычисляются по формуле:

, где - элемент i-ой строки и j-го столбца;

- разрешающий элемент;

- элемент разрешающей строки j-го столбца;

- элемент разрешающего столбца i-ой строки.

Получаем следующую симплекс-таблицу.

.

Так как в f-строке имеется отрицательный элемент, то план не является оптимальным. Улучшаем по той же схеме, как делали выше. Столбец с переменной будет разрешающим. Среди симплексных отношений определяем наименьшее: . Возьмем за разрешающий элемент . Из базисных переменных исключаем переменную и вносим переменную . Далее делаем преобразования по правилу ПОЗ. Получаем следующую симплекс-таблицу.

.

В таблице в -строке нет отрицательных элементов, значит, построенный план является оптимальным, и к тому же единственный (нет нулевых элементов в -строке):

.

Целевая функция принимает значение ден.ед.

Оптимальный план показывает, что продукцию вида П₂ выпускать нецелесообразно, продукцию вида П₁ выпускать в объеме 1 единица, продукцию вида П₃ – в объеме 1 единица.

На выпуск продукции вида П₁ используется 2 единицы ресурсов Р₂ и 1 единица ресурсов Р₃. На выпуск продукции вида П₃ используется 5 единиц ресурсов Р₁, 2 единицы ресурсов Р₂ и 1 единица ресурсов Р₃.

При этом каждого вида ресурса использовано полностью: Р₁ - 5 единиц, Р₂ – 2+2=4 единицы, Р₃ – 1+1=2 единицы.

Ответ: , ден.ед.



Базисный план ЗЛП, записанный в предпочтительном виде, невырожден, когда свободные члены всех уравнений положительны, и вырожден, если среди них имеются нули. Каноническую ЗЛП называют невырожденной, если все ее опорные планы невырождены. Если среди опорных планов есть хотя бы один вырожденный, то задачу называют вырожденной.

Если ЗЛП вырожденная, то значение целевой функции не улучшается. Предположим, что процесс продолжается без остановки, порождая бесконечную последовательность опорных планов. Вследствие конечности множества опорных планов в этой последовательности некоторые планы должны повторяться. В силу равенства для них целевой функции они должны лежать в одной гиперплоскости и быть вершинами выпуклого многогранника. Поэтому должна встретиться цепочка (цикл) , в которой начальный и конечный планы совпадают, причем в силу монотонности метода

.

Процесс продолжается неограниченно, если несколько последовательных вырождений приведет к образованию цикла. Такое явление называется зацикливанием. Зацикливание возможно только для вырожденных задач. Теория и практика показывают, что зацикливание возникает при весьма маловероятном сочетании условий. Известно лишь несколько специально разработанных (очень сложных) примеров, в процессе решения которых возникает зацикливание. Точный алгоритм вывода из цикла достаточно сложен. В простейшем случае при появлении цикла следует изменить последовательность вычислений путем изменения выбора разрешающего столбца. Другое правило рекомендует изменить выбор разрешающей строки. Если в процессе симплексных преобразований появляется несколько минимальных симплексных отношений, то в качестве разрешающей выбирают ту строку, для которой будет наименьшим отношение элементов первого столбца к разрешающему. Если при этом снова оказывается несколько минимальных отношений, то составляются отношения элементов второго столбца к разрешающему, и так до тех пор, пока разрешающая строка не определится однозначно.