4. Свойства решений злп

Пусть ЗЛП представлена в следующей записи:

; (2.27)

, (2.28)

. (2.29)

Чтобы задача (2.27) – (2.29) имела решение, система ее ограничений (2.28) должна быть совместной. Это возможно, если ранг системы (число линейно независимых уравнений) не больше числа неизвестных . Случай вообще невозможен. При система имеет единственное решение, которое и будет при оптимальным. В этом случае проблема выбора оптимального решения теряет смысла.

Выясним структуру координат угловой точки многогранника решений. Пусть . В этом случае система векторов содержат базис – максимальную линейно независимую подсистему векторов, через которую любой вектор системы может быть выражен как ее линейная комбинация. Базисов, вообще говоря, может быть несколько, но не более . Каждый из них состоит точно из векторов. Переменные ЗЛП, соответствующие векторам базиса, называют базисными и обозначают БП. Остальные переменных будут свободными, их обозначают СП.

Не ограничивая общности, будем считать, что базис составляют первые векторов . Этому базису соответствуют базисные переменные , а свободными будут переменные .

Если свободные переменные приравнять нулю, а базисные переменные при этом примут неотрицательные значения, то полученное частное решение система (2.28) называют опорным решением (планом).

Сформулируем (без доказательства) следующую теорему.

Теорема 2.2. Если система векторов содержит линейно независимых векторов , то допустимый план является крайней точкой многогранника планов.

Итак, если допустимый план имеет положительных координат, а все остальные координаты равны нулю, то это опорный план ЗЛП. Если положительных координат меньше , а все остальные равны нулю, то такой план называется вырожденным опорным планом. Если же допустимый план имеет больше положительных координат, то он вообще не соответствует крайней точке многогранника и не является опорным планом.

Сформулируем основную теорему линейного программирования (без доказательства).

Теорема 2.3. Если ЗЛП имеет решение, то целевая функция достигает экстремального значения хотя бы в одной из крайних точек многогранника решений. Если же целевая функция достигает экстремального значения более чем в одной крайней точке, то она достигает того же значения в любой точке, являющейся их выпуклой линейной комбинацией.

5. Симплексный метод

Анализируя решение приведенных выше примеров, заметим, что для ЗЛП с двумя переменными экстремум достигается в вершине области допустимых решений.

Следует отметить, что, независимо от числа переменных, экстремум целевой функции достигается в вершине многогранника планов решений ЗЛП или, если эта вершина не является единственной, в точках, являющихся выпуклой линейной комбинацией вершин, где достигается экстремум. В результате возникает способ решения ЗЛП любой размерности, который заключается в том, чтобы найти каким-нибудь образом все крайние точки многогранника планов, их не больше, чем 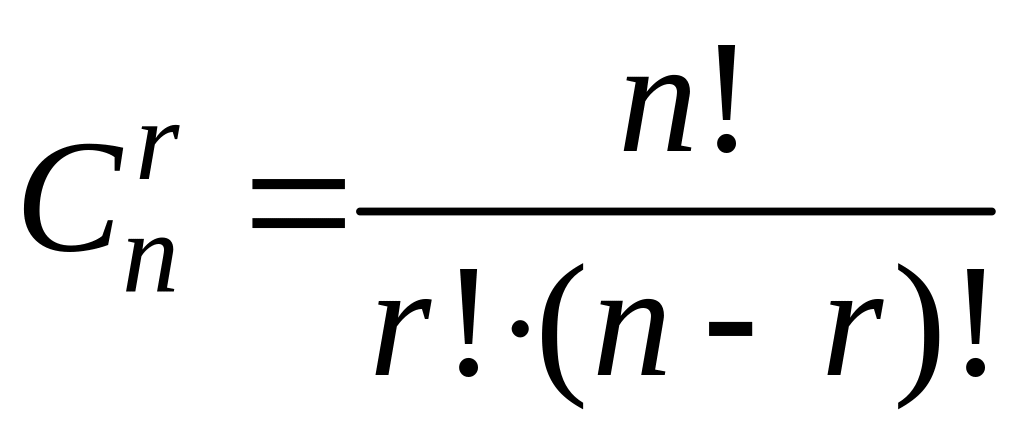, и сравнить в них значения целевой функции. Однако, такой путь решения даже с относительно небольшим числом переменных и ограничений практически неосуществим, так как процесс отыскания крайних точек сравним по трудности с решением исходной задачи, к тому же число крайних точек многогранника планов может оказаться весьма большим. В связи с этим возник метод рационального перебора крайних точек. Суть его в следующем. Если известны какая-нибудь крайняя точка и значение в ней целевой функции, то все крайние точки, в которых целевая функция принимает худшее значение, заведомо не нужны. Тогда естественно стремление найти способ перехода от данной крайней точки к лучшей, которая смежная с данной по ребру, от нее к еще лучшей (не худшей) и т.д. Для этого нужно иметь признак того, что лучших крайних точек, чем данная крайняя точка вообще нет. В этом и состоит идея наиболее широко применяемого в настоящее время симплексного метода (метода последовательного улучшения плана) для решения ЗЛП. Итак, в алгебраических терминах симплексный метод предполагает: 1) умение находить начальный опорный план; 2) наличие признака оптимальности опорного плана; 3) умение переходить к нехудшему опорному плану.

На базе этого метода составлен ряд компьютерных программ по оптимизации ЗЛП.