Основные теоремы двойственности и их экономическое содержание
Сформулируем основные теоремы двойственности (без доказательства).
Теорема 3.4 (первая теорема двойственности).
Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций равны . Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.
Экономическое содержание первой теоремы двойственности состоит в следующем: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукции, полученной при реализации оптимального плана, совпадает с суммарной оценкой ресурсов. Совпадение значений целевых функций для соответствующих планов пары двойственных задач достаточно для тог, чтобы эти планы были оптимальными. Это значит, что план производства и вектор оценок ресурсов являются оптимальными тогда и только тогда, когда цена произведенной продукции и суммарная оценка ресурсов совпадают. Оценки выступают как инструмент балансирования затрат и результатов. Двойственные оценки гарантируют рентабельность оптимального плана, т.е. равенство общей оценки продукции и ресурсов, и обусловливают убыточность всякого другого плана, отличного от оптимального. Двойственные оценки позволяют сопоставить и сбалансировать затраты и результаты системы.
Теорема 3.5 (о дополнительной нежесткости, вторая теорема двойственности).
Для того чтобы планы и пары двойственных задач были оптимальными, необходимо и достаточно выполнение условий:
,
.
Эти условия называются условиями дополнительной нежесткости. Из них следует: если какое-либо ограничение одной из задач ее оптимальным планом обращается в строгое неравенство, то соответствующая компонента оптимального плана двойственной задачи должна равняться нулю; если же какая-либо компонента оптимального плана одной из задач положительна, то соответствующее ограничение в двойственной задаче ее оптимальным планом должно обращаться в строгое равенство.
Таким образом, если
,
то
;
если
,
то
.
Точно так же, если
,
то
;
если
,
то
.
Экономически это означает, что если по некоторому оптимальному плану производства расход -го ресурса строго меньше его запаса , то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса равна нулю. Если же в некотором оптимальном плане оценок его -ая компонента строго больше нуля, то в оптимальном плане производства расход соответствующего ресурса равен запасу. Отсюда следует вывод: двойственные оценки могут служить мерой дефицитности ресурсов; дефицитный ресурс (полностью используемый по оптимальному плану производства) имеет положительную оценку, а ресурс избыточный (используемый не полностью) имеет нулевую оценку.
Теорема 3.6 (об оценках, третья теорема двойственности).
В оптимальном решении двойственной
задачи значения переменных
(оценки) численно равны частным производным
для исходной задачи, т.е.
.
(3.8)
Двойственные оценки показывают приращение функции, вызванное малым изменением свободного члена соответствующего ограничения задачи линейного программирования.
Перейдем к выяснению экономического
содержания третьей теоремы двойственности.
Для этого в равенстве (3.8) дифференциалы
заменим приращениями. Получаем
.
При
имеем
.
Отсюда величина двойственной оценки
численно равна изменению целевой функции
при изменении соответствующего свободного
члена ограничений на единицу. В прикладных
задачах двойственные оценки
часто называют скрытыми, теневыми
ценами или маргинальными оценками
ресурсов.
Пример 3.4. Используя условие примера 2.11:
1) сформулировать в экономических терминах двойственную задачу и составить ее математическую модель;
2) используя решение примера 2.11 и
соответствие между двойственными
переменными, найти компоненты оптимального
плана двойственной задачи – двойственные
оценки
.
Решение. Математическая модель прямой задачи (смотри пример 2.11) имеет вид:
;
.
Или с учетом введения балансовых неотрицательных переменных , и :
;
.
1) Сформулируем в экономических терминах двойственную задачу и составим ее математическую модель.
Пусть на предприятии появилась возможность продать ресурсы некоторой организации. Необходимо установить цены на эти ресурсы. Обозначим их через . Цены должны быть установлены исходя из следующих требований, отражающих несовпадающие интересы предприятия и организации:
а) покупающая организация стремится минимизировать общую стоимость ресурсов, т.е.
;
б) предприятие согласно продать только по таким ценам, при которых оно получит за них выручку, не меньшую той, что могло бы получить, организовав собственное производство, т.е.
.
Таким образом, математическая модель двойственной задачи имеет вид:
;
.
2) Поскольку прямая задача имеет
оптимальное решение, то и двойственная
ей задача будет иметь оптимальное
решение. В систему ограничений двойственной
задачи введем балансовые неотрицательные
переменные
.
Установим соответствие между переменными прямой и двойственной задачи
Используя решение прямой задачи и полученное соответствие между переменными, найдем оптимальный план двойственной задачи.
.
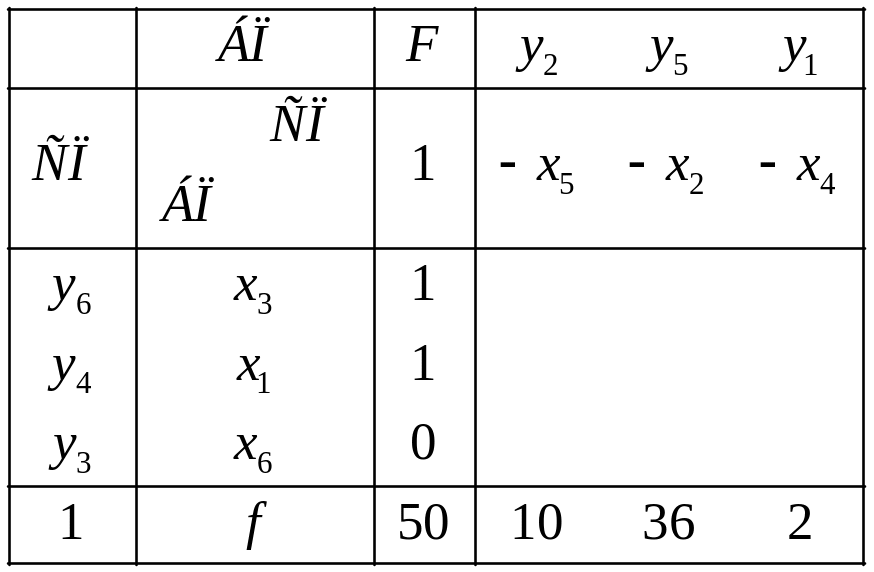Оптимальный план двойственной задачи
;
(ден.ед.).
Согласно полученным результатам имеем: ресурс первого вида должен стоить 2 ден.ед., ресурс второго вида – 10 ден.ед. При этом покупающая организация затратит минимальное количество денег на приобретение ресурсов, которое составит 50 ден.ед.
Ответ:
,
ден.ед.