Симплексный метод

Симплексный метод является универсальным методом решения задач моделей линейной оптимизации:

F = c₁x₁ + c₂x₂ + … + c_nx_n  max (min)

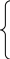a₁₁x₁ + a₁₂x₂ + … + a_1nx_n  () b₁,

a₂₁x₁ + a₂₂x₂ + … + a_2nx_n  () b₂,

… … … … … … …

a_m1x₁ + a_m2x₂ + … + a_mnx_n  () b_m,

x_j  0, j = 1, 2, …, n.

Алгоритм решения задачи симплексным методом:

1. Приведем задачу линейного программирования к каноническому виду. При необходимости перехода от неравенства к уравнению вводят дополнительные переменные.

Так, неравенство a_i1x₁ + a_i2x₂ + … + a_inx_n  b_i заменяется уравнением a_i1x₁ + a_i2x₂ +…+ a_inx_n + x_n+1 = b_i и условием неотрицательности дополнительной переменной x_n+1  0. А неравенство вида a_i1x₁ + a_i2x₂ + … + a_inx_n  b_i заменяется уравнением a_i1x₁ + a_i2x₂ + … + a_inx_n  x_n+1 = b_i и условием неотрицательности дополнительной переменной x_n+1  0.

После введения добавочных переменных систему уравнений и линейную функцию записываем в виде расширенной системы:

a₁₁x₁ + a₁₂x₂ + … + a_1nx_n + x_n+1 = b₁,

a₂₁x₁ + a₂₂x₂ + … + a_2nx_n + x_n+2 = b₂,

… … … … … … …

a_m1x₁ + a_m2x₂ + … + a_mnx_n + x_n+m = b_m,

F – c₁x₁ – c₂x₂ – … – c_nx_n = 0.

Если в каком-либо уравнении правая часть отрицательна, то это уравнение нужно умножить на (–1). Предполагаем, что все дополнительные переменные имеют тот же знак, что и свободные члены. Дополнительные переменные вводят в целевую функцию с коэффициентами, равными нулю. Система ограничений является системой m линейных уравнений с n неизвестными, и все n переменных неотрицательные ( m < n ).

Любые m переменных системы m линейных уравнений с n переменными называются базисными (или основными), если определитель матрицы коэффициентов при этих переменных отличен от нуля. Остальные n – m переменных называются свободными. Базисным решением называется всякое решение системы линейных уравнений, в котором свободные переменные имеют нулевые значения. Базисное решение системы линейных уравнений называется допустимым, если все его компоненты не отрицательны. Такое допустимое решение называют опорным решением, или опорным планом.

2. Находим допустимое базисное решение. Полученную расширенную систему заносим в первую симплексную таблицу. Последняя строка таблицы, в которой приведено уравнение для линейной функции, называется оценочной. В ней указываются коэффициенты целевой функции с противоположным знаком: . В левом столбце таблицы записываем основные переменные (базис), в заголовке таблицы заносим все переменные; во втором столбце – свободные члены расширенной системы b₁, b₂, …, b_m. Последний столбец подготовлен для оценочных отношений, необходимых при расчете наибольшего возможного значения переменной. В рабочую часть таблицы (начиная с третьего столбца) занесены коэффициенты при всех переменных из расширенной системы.

3. Найденный опорный план проверяем на выполнение критерия оптимальности при решении задачи на максимум – наличие в последней строке отрицательных коэффициентов. Если таких коэффициентов нет, то решение оптимально, достигнут max F = с_о (в левом нижнем углу таблицы), основные переменные принимают значения, записанные во втором столбце, а не входящие в базис переменные равны 0, т.е. получаем оптимальное базисное решение.

4. Если критерий оптимальности не выполнен, то наибольший по модулю отрицательный коэффициент в последней строке определяет разрешающий столбец s.

Составляем оценочные отношения для каждой строки по следующим правилам:

1) , если и ;

2) , если ;

3) 0, если и ;

4) , если и имеют одинаковые знаки.

Определяем . Если конечного минимума нет, то задача не имеет конечного оптимума . Если минимум конечен, то выбираем строку q, на которой он достигается (любую, если их несколько), и называем ее разрешающей строкой. На пересечении разрешающих строки и столбца находится разрешающий элемент .

5. Переходим к новому опорному плану. Базисное решение можно найти по правилу прямоугольника или с помощью преобразований Жордана–Гаусса.

Правило прямоугольника

Следующую таблицу заполняем по правилам:

а) в левом столбце записываем новый базис: вместо основной переменной – переменную ;

б) в столбцах, соответствующих основным переменным, проставляем нули и единицы: 1 – против “своей” основной переменной, 0 – против “чужой” основной переменной, 0 – в последней строке для всех основных переменных;

в) новую строку с номером q получаем из старой строки делением на разрешающий элемент ;

г) все остальные элементы вычисляем по правилу прямоугольника:

Далее переходим к п. 3 алгоритма.

Преобразования Жордана-Гаусса

Данный метод решения систем линейных уравнений основан на понятии эквивалентности систем уравнений. Две системы из m уравнений с n неизвестными называются эквивалентными, если имеют одни и те же решения. Следующие операции позволяют одну систему уравнений преобразовать в эквивалентную ей:

а) любые два уравнения можно менять местами;

б) уравнения можно умножать на любую постоянную величину, не равную нулю;

в) любое уравнение, умноженное на ненулевую константу, можно почленно складывать с другими уравнениями системы.

Нам необходимо получить новый опорный план, который отличается от первоначального тем, что в нем в левом столбце таблицы записываем новый базис: вместо основной переменной – переменную . Для того, чтобы переменная стала базисной, необходимо в столбец s получить единицу на месте разрешающего элемента , а все остальные элементы этого столбца сделать нулевыми. Это делается с помощью преобразований Жордана–Гаусса, которые состоят из следующих шагов:

а) разделим или умножим строку, содержащую разрешающий элемент , на такое число, чтобы стал равен единице, и запишем полученное урав-

нение в новую симплекс-таблицу.

б) умножим новую строку на постоянные различные числа и сложим почленно с остальными строками таблицы для того, чтобы в столбце s получить нули. Результат запишем в соответствующие строки новой симплекс-таблицы.

Далее переходим к п. 3 алгоритма.

Пример 4. Решить задачу об оптимальном использовании сырья симплексным методом.

Для изготовления четырех видов продукции предприятие ис­пользует три типа ресурсов. Нормы расхода ресурсов каждого типа на единицу продукции, их наличие в распоряжении предприятия, а также цена единицы продукции приведены в табл. 6.

Таблица 6

Тип ресурса	Нормы расхода ресурсов на единицу продукции				Наличие ресурса
	А	B	C	D
1 2 3	1 0 4	0 1 2	2 3 0	1 2 4	180 210 800
Цена единицы продукции	9	6	4	7

Определить, сколько продукции каждого вида следует производить, если цель предприятия состоит в максимизации прибыли (сбыт продукции обеспечен). Дать экономическую интерпретацию всех переменных симплексных таблиц.

Решение. Составим экономико-математическую модель задачи. Обозначим x₁, x₂, x₃, x₄ – число единиц продукции соответствующего вида A, B, C, D, запланированных к производству. Поскольку имеются ограничения на размеры допустимых затрат ресурсов, то переменные x₁, x₂, x₃, x₄ должны удовлетворять системе неравенств:

(1)

По смыслу задачи переменные удовлетворяют условию неотрицательности:

x₁, x₂, x₃, x₄  0. (2)

Суммарная прибыль от реализации продукции составит:

F = 9 x₁ + 6 x₂ + 4 x₃ + 7 x₄. (3)

Итак, требуется найти такой план выпуска продукции X = (x₁, x₂, x₃, x₄), удовлетворяющий системе (1) и условию (2), при котором функция (3) принимает максимальное значение

После введения дополнительных переменных систему уравнений и линейную функцию запишем в виде расширенной системы:

Эти дополнительные переменные по экономическому смыслу означают не используемое при данном плане производства количество сырья соответствующего вида.

Заполняем первую симплексную таблицу (табл. 7), в которой переменные x₅, x₆, x₇ берем за базисные. Последняя строка заполняется коэффициентами линейной функции с противоположным знаком (см. п. 2 алгоритма).

Таблица 7

Б азис	Свободный член	Переменные							Оценочное отношение	Уравнение
		основные				дополнительные
		x1	x2	x3	x4	x5	x6	x7
x5	180	1	0	2	1	1	0	0	180
x6	210	0	1	3	2	0	1	0	∞
x7	800	4	2	0	4	0	0	1	200
F	0	– 9	– 6	– 4	– 7	0	0	0

Данные столбцов, соответствующих переменным x₁, x₂, х₃, x₄ – это технико-экономические показатели, норма затрат соответствующего вида сырья на производство единицы продукции. Как видно из табл. 7, значения всех основных переменных x₁, x₂, х₃, x₄ равны нулю, а дополнительные переменные принимают свои значения в соответствии с ограничениями задачи. Эти значения переменных отвечают такому "плану", при котором ничего не производится, сырье не используется и значение целевой функции равно нулю (т.е. стоимость произведенной продукции отсутствует). Этот план, конечно, не является оптимальным.

Это видно и из 4-й строки табл. 7, так как в ней имеются четыре отрицательных числа: . Отрицательные числа не только свиде-тельствуют о возможности увеличения общей стоимости производимой продукции, но и показывают, на сколько увеличится прибыль при введении в план единицы того или другого вида продукции. Так, число – 9 означает, что при включении в план производства одного изделия вида А обеспечивается увеличение общей стоимости выпускаемой продукции на 9 денежных единиц. Если включить в план производства по одному изделию В и С или D, то общая стоимость изготовляемой продукции возрастет соответственно на 6 и 4, или 7 денежных единиц. Поэтому с экономической точки зрения наиболее целесообразным является включение в план производства изделия вида А.

Это же необходимо сделать и на основании формального признака симплексного метода. В соответствии с п. 3 алгоритма проверяем критерий оптимальности. В последней строке имеются отрицательные коэффициенты. Выбираем из них наибольший по модулю (–9), следовательно, первый столбец разрешающий, переменная x₁ перейдет в основные переменные (этот столбец отмечен стрелкой).

В соответствии с п. 4 алгоритма находим оценочные отношения и выбираем . Первая строка является разрешающей (отмечена горизонтальной стрелкой). На пересечении разрешающих строки и столбца стоит разрешающий элемент .

Найдя число 180, мы тем самым с экономической точки зрения определили какое количество изделий А предприятие может изготовлять с учетом норм расхода и имеющихся объемов сырья каж­дого вида. Так как сырья данного вида соответственно имеется 180, 210 и 800 единиц, а на одно изделие А требуется затратить сырья каждого вида соответственно 1, 0 и 4 единиц, то максимальное число изделий А, которое может быть изготовлено предприятием, равно . То есть, ограничивающим фактором для производства изделий А является имеющийся объем сырья I вида. С учетом его наличия предприятие может изготовить 180 изделий А. При этом сырье I вида будет полностью использовано. Следовательно, переменная x₅, подлежит исключению из базиса.

В соответствии с п. 5 алгоритма переходим к новому опорному плану. Строим симплексную табл. 5. Новое базисное решение системы найдем либо по правилу прямоугольника, либо с помощью преобразований Жордана-Гаусса:

Правило прямоугольника

а) в новом базисе основные переменные: x₁, x₆, x₂;

б) расставляем нули и единицы. Например, в клетке, соответствующей основной переменной х₁ по столбцу и строке, ставим 1, а в клетке, соответствующей основной переменной х₁ по строке и основной переменной х₆ – по столбцу, ставим 0 и т.п. В последней строке против всех основных переменных ставим 0;

в) первая строка получается делением на разрешающий элемент ;

г) остальные клетки заполняем по правилу прямоугольника. Получим:

Преобразования Жордана-Гаусса

Строим вторую симплексную таблицу (табл. 8), в левом столбце которой вместо исключаемой переменной запишем новую базисную переменную .

Таблица 8

Базис	Свобод. член	Переменные							Оценочное отношение	Уравнение
		x1	x2	x3	x4	x5	x6	x7
x1	180	1	0	2	1	1	0	0	∞
x 6	210	0	1	3	2	0	1	0	210
x 7	80	0	2	– 8	0	– 4	0	1	40
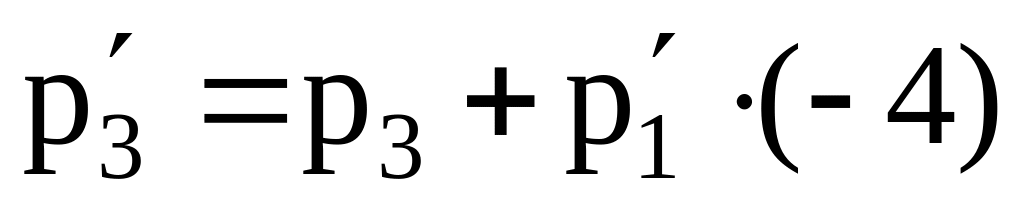
F	1620	0	– 6	14	2	9	0	0

В новой симплекс-таблице столбец при должен стать единичным (разрешающий элемент – равняться единице, а все остальные элементы – обратиться в ноль). Это достигается следующими преобразованиями строк табл. 7:

а). Первую строку из табл. 7 запишем в первую строку новой симплекс-таблицы без изменений, так как разрешающий элемент .

.

б). Вторую строку также перепишем, так как .

.

в). К третьей строке прибавим новую первую строку, умноженную на – 4, чтобы элемент, стоящий в разрешающем столбце обратился в ноль. Результат запишем в третью строку новой симплекс–таблицы.

.

г). Умножим новую первую строку на 9, сложим почленно с четвертой строкой и результат запишем в четвертую строку новой симплекс-таблицы.

.

Как видно из этой таблицы, новым опорным планом задачи является план Х= (180, 0, 0, 0, 0, 210, 80). При данном плане производства изготовляет­ся 180 изделия вида A и остается неиспользованным 210 единиц сырья II–го вида и 80 единиц сырья III вида. Стоимость всей производимой при этом плане продукции равна 1620 денежных единиц. Указанные числа записаны в столбце свободных членов табл. 8. Как видно, данные этого столбца по-прежнему представляют собой исходные параметры рассматриваемой задачи, хотя они претер­пели изменения.

Экономический смысл элементов столбца x₂ не изменился.

Данные в других столбцах изменились, а их экономическое содержание стало более сложным. Так, например, возьмем данные столбца x₃. Число 2 во 1-й строке этого столбца показывает, на сколько следует уменьшить изготовление изде­лий A, если запланировать выпуск одного изделия вида C. Число 3 во 2-й строке переменной x₃ показывает, сколько потребуется сырья II вида при включении в план производства одного изделия вида C, а число – 8 в 3-й строке – на сколько увеличится количество неиспользуемого сырья III вида.

Число 14 в 4-ой строке показывает, что если будет запланирован выпуск одного изделия вида C, то это приведет к уменьшению выпуска продукции в стоимостном выражении на 14 денежных единиц. Иными слова­ми, если включить в план производства продукции одно изделие C, то это потребует уменьшения выпуска изделия A на 2 единицы и потребует дополнительных затрат 3 единиц сырья II вида, но увеличение остатка сырья III вида на 8 единиц, а общая стоимость изготовляемой продукции в соответствии с новым планом уменьшится на 8 руб.

Таким образом, числа 3 и – 8 выступают как бы новыми "нормами" затрат сырья II и III вида на изготовление одного изделия C (как видно из табл. 7, ранее они были равны 3 и 0, что объясняется уменьшением выпуска изделий вида A).

Несколько иное экономическое содержание имеют числа, записанные в столбце переменной x₅. Число 1 в 1-й строке этого столбца показывает, что увеличение объемов сырья I вида на 1 единицу позволило бы увеличить выпуск изделий A на 1 единицу. Для этого потребо­валось бы дополнительно 4 единицы сырья III вида. Увеличение выпуска изделий A на 1 единицу приведет к росту выпуска продукции в стоимостном выражении на 9 денежных единиц. Из изложенного выше экономического содержания данных табл. 8 следует, что найденный на второй итерации план задачи не является опти­мальным.

Это видно и из 4-й строки табл. 8, поскольку в столбце переменной x₂ этой строки стоит отрицательное число – 6. Значит второй столбец разрешающий, в базис следует ввести переменную x₂, то есть в новом плане следует предусмотреть выпуск изделий В.

При определении возможного числа изготовления изделий В следует учитывать имеющееся количество сырья каждого вида, а именно: возможный выпуск изделий В определяется . Следовательно, исключению из базиса подлежит переменная x₇, иными словами, выпуск изделий В ограничен имеющимся в распоряжении предприятия сырьем III вида. С учетом имеющихся объемов этого сырья предприятию следует изготовить 40 изделий В. Третья строка табл. 8 является разрешающей, а – разрешающим элементом.

Новая симплексная таблица примет вид табл. 9.

Таблица 9

Базис	Свобод. член	Переменные							Оценочное отношение	Уравнение
		x1	x2	x3	x4	x5	x6	x7
x 1	180	1	0	2	1	1	0	0	180
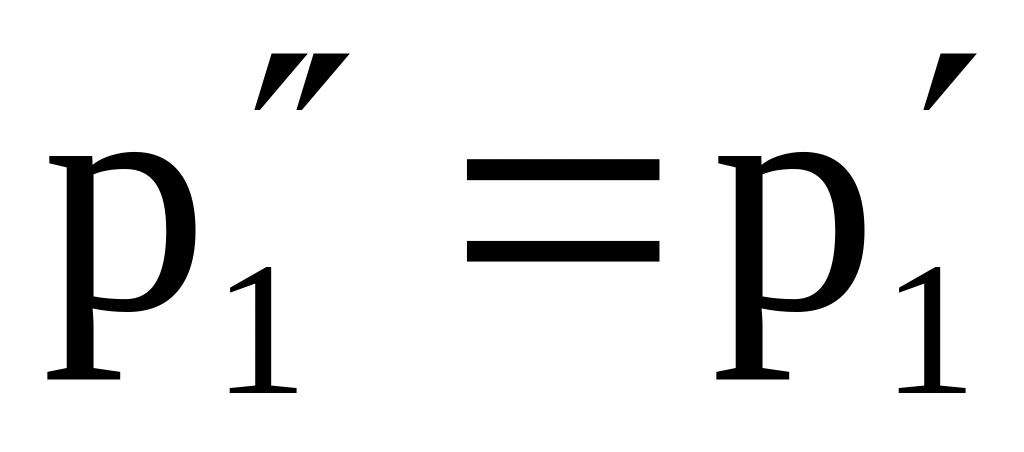
x 6	170	0	0	7	2	2	1	–1/2	85
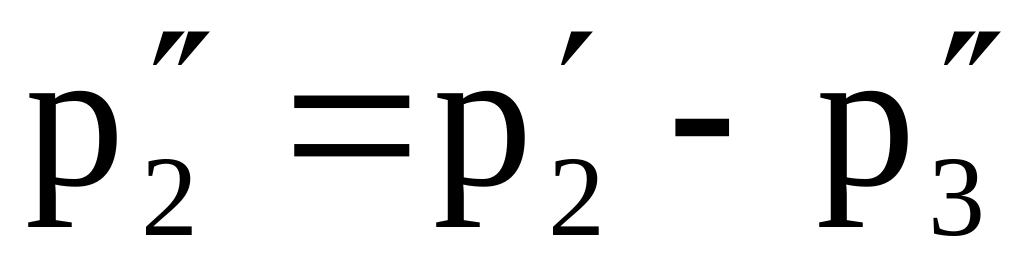
x2	40	0	1	– 4	0	– 2	0	1/2
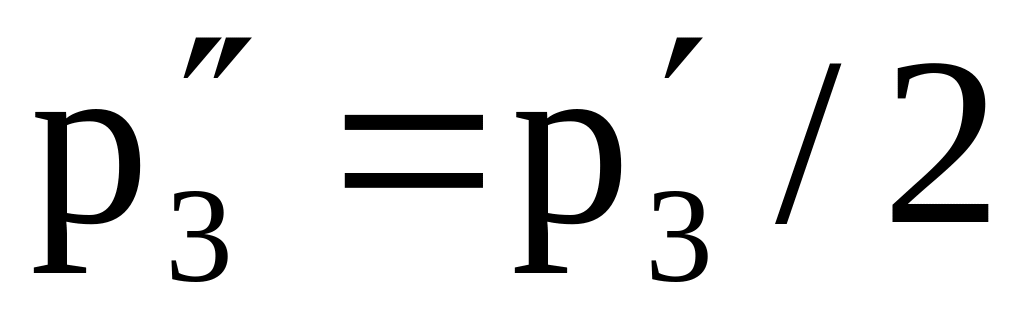
F	1860	0	0	–10	2	– 3	0	3

И на этот раз критерий оптимальности не выполнен: имеем два отрицательных элемента. Для простоты вычислений выберем в качестве разрешающего пятый столбец; вторая строка разрешающая, следовательно, – разрешающий элемент.

Переходим к следующей табл. 10.

В результате получен новый опорный план Х = (95, 210, 0, 0, 85 , 0, 0).

Проверяем, является ли данный опорный план оптимальным или нет. Для этого рассмотрим 4-ю строку табл. 10. В этой строке нет отрицательных чисел. Это означает, что найденный опорный план Х^*= (95, 210, 0, 0, 85 , 0, 0) является оптимальным и max F = 2115.

Таблица 10

Базис	Свободный член	Переменные							Уравнение
		основные				дополнительные
		x1	x2	x3	x4	x5	x6	x7
x1	95	1	0	–3/2	0	0	–1/2	1/4
x5	85	0	0	7/2	1	1	1/2	–1/4
x2	210	0	1	3	2	0	1	0
F	2115	0	0	1/2	5	0	3/2	9/4

Следовательно, план выпуска продукции, включающий изготовле­ние 95 изделий A и 210 изделий B, является оптимальным. При данном плане выпуска продукции полностью используется сырье II и ПI видов и остается неиспользованным 85 единиц сырья I вида, а стоимость произво­димой продукции равна 2115 денежных единиц.

Оптимальным планом производства продукции не предусматривает­ся изготовление изделий C и D. Введение в план выпуска продукции изделий, например, вида C привело бы к уменьшению указанной общей стоимо­сти. Это видно из 4-й строки столбца переменной x₃, где число 1/2 показы­вает, что при данном плане включение в него выпуска единицы изде­лия вида C приводит к уменьшению общей величины стоимости на 1/2 денежных единиц. Это происходит за счет уменьшения выпуска продукции вида B на 3 единицы (как показывает число 3 в третьей строке столбца переменной x₃), хотя производство продукции вида A при этом и увеличивается на 3/2, как показывает число в первой строке столбца переменной x₃.

Увеличение объема сырья первого вида на единицу не повлияет на изменение максимального значения целевой функции, не приведет к изменению оптимального плана выпуска продукции, лишь увеличит остаток этого сырья на единицу. Это показывают значения столбца переменной x₅.

Увеличение, например, объема сырья второго вида на единицу приведет к увеличению максимального значения целевой функции на 3/2 денежных единицы за счет возможности увеличения выпуска продукции вида В на 1, хотя при этом выпуск продукции вида уменьшится на 1/2, как показывают значения столбца переменной x₆.