
- •Величины, их единицы измерения и соотношения между ними (длина, масса, время, емкость, площадь).
- •Методика обучения решению текстовых задач.
- •Понятие «задача» в начальном
- •Классификация задач.
- •Приемы организации деятельности учащихся, направленные на формирование умения решать задачи.
- •Рассмотрим методику работы над задачами
- •I подход Методика работы над задачами, раскрывающими
- •Задачи, раскрывающие конкретный смысл умножения
- •Задачи, раскрывающие конкретный смысл деления
- •Методика работы над задачами, раскрывающими
- •Задача №9
- •II подход.
- •Методика работы над составными типовыми задачами
Доли величины. Дроби.
В соответствии с программой по математике в начальных классах должна быть проведена подготовка к изучению дробей в 5 классе. Это значит, что в начальных классах надо создать конкретные представления о доле и дроби.
Задачи изучения темы:
Познакомить с понятием "доля" , с образованием и обозначением долей.
Научить сравнивать доли.
Формировать умения решать задачи на нахождение доли числа и числа по доле. Отличительной особенностью данной темы является её конкретность, наглядность, иллюстративность. При сообщении сведений о долях целесообразней провести как можно больше практических работ.
Порядок изучения темы:
Выявление имеющихся представлений о долях. Как получить половину яблока? круга? квадрата? полоски?
Образование долей.
Для лучшего усвоения понятия доли на первом уроке полезно рассмотреть деление реального предмета на части (апельсин, яблоко), затем деление отвлеченных предметов (геометрических фигур).
Учитель берёт модель круга и складывает его пополам так, чтобы все видели как совпали края половинок. Разрезаем круг пополам.
-Это половина круга или одна вторая круга.
-Сколько половин (вторых долей) в целом круге? Как получить одну вторую долю
квадрата, прямоугольника?
3. Обозначение долей.
Доли записывают с помощью двух чисел: 1V2. Термины «числитель» и «знаменатель» по традиционной программе не вводятся, по другим даются. Учитель обобщает, что, если круг разделили на 3 равные части и нужно обозначить 1\3 долю, то проводят черту, число под чертой показывает на сколько частей разделили, под чертой сколько таких частей взяли.
4. Сравнение долей.
Сравнение проводится чисто практически с использованием моделей фигур или чертежа Можно предложить детям начертить 4 полоски одинаковой длины. На одной раскрасить половину, на второй 1\3, на третьей 1\4, на четвертой 1\8. Убеждаются , что самая крупная 1\2, самая мелкая 1\8. Запись: 1\2 >1\8. Делается общий вывод: из двух долей с одинаковыми числителями, но разными знаменателями больше та, у которой знаменатель меньше.
Решение задач.
Первыми вводятся задачи на нахождение доли числа.
Например. От ленты длиной 12 см отрезали 1\3 часть. Чему равна длина отрезанной части?
В качестве модели ленты используют полоску длиной 12 см.
— Как найти 1\3?
- Перегните полоску. Отрежьте 1\3 часть.
Затем полоску изображают отрезком.
Запись решения и ответа.
Делается вывод: задачи на нахождение доли числа решаются делением.
Выполняются задания вида: Сколько см в 1\2 м , в 1\4 м? Сколько минут в 1\2 часа? Далее вводятся задачи на нахождение числа по доле.
Например. Длина 1\3 ленты 10 см. Узнай длину всей ленты?
Изобразите ленту отрезком ( 10 см ).
Какая часть ленты известна ?
Как изобразить всю ленту?
Почему? Начертите.
Какой длины была лента ? Как нашли?
Делается вывод: задачи на нахождение числа по его доле решаются умножением.
На основе изучения данной темы вводится «Дробь числа».
Задачи изучения темы:
Познакомить с понятием «дробь».
Учить получать, читать, записывать обыкновенные дроби со знаменателем, не превышающим число сто.
Формировать умение решать задачи на нахождение дроби числа и числа по дроби. Работа ведется по следующему плану.
1. Подготовительный этап.
Обобщение представлений о доле как одной из равных частей.
2. Ознакомление. Образование дроби.
Возьмите круг. Разделите его на 4 равные части.
Как назвать каждую такую часть. Запишите.
Покажите 3\4 доли. Вы получили дробь 3\4.
Запишите её. Что показывает число 4?3?
Обозначение дробей.
Сравнение дробей.
Для сравнения используются иллюстрации с равными прямоугольниками.
-
1
1\2
1\2
1\4
1\4
1\4
1\4
1\8
1\8
1\8
1\8
1\8
1\8
1\8
1\8
Сколько вторых долей в прямоугольнике?
Какие еще доли получили?
Сколько четвертых долей в целом прямоугольнике? В половине?
Что больше 1V2 или 1\4, 1\2 и 2\4, 1\4 и 3\4 и т.д.
Таким образом, устанавливается, что единица содержит 2 половины(4\4, 8\8), что 1 \4 может быть получена делением 1\2 на 2 равные части или сложением. Дети убеждаются, что 1\2=2\4, 1\4=2\8. Так сравниваются дроби со знаменателями 2,4,8. затем 2,5,10 и 3,6,9. Для каждого случая выполняются различные иллюстрации.
Делаются выводы: Для двух дробей с одинаковыми числителями, но разными знаменателями больше та дробь, у которой знаменатель меньше.
Для двух дробей с разными числителями, но одинаковыми знаменателями больше та дробь, у которой числитель больше.
5. Далее конкретный смысл дроби раскрывается при решении задач на нахождение дроби числа.
Например. «У портнихи было 12 метров ленты. 2\3 ленты она отрезала на платье. Сколько метров ленты отрезала портниха?»
На чертеже изобразим всю ленту отрезком 12см, приняв 1м=1см.
Какой длины отрезок надо начертить?
Сколько метров отрезали?
Что узнаем сначала?
Как?
-Что узнаем затем ? Как?
(Чему равны 2\3 ленты. Умножением.)
- Сколько метров ленты отрезала портниха?

Затем решаются задачи на нахождение числа по его дроби.
Например. Задача. От куска проволоки отрезали 12 метров , что составляет ¾ длины всей проволоки. Найти длину всей проволоки?
Изобразим длину всей проволоки отрезком:

- Какова длина всего отрезка?
- Что обозначает число 12?
- Как изобразить на отрезке 12 метров?
(Разделить отрезок на 4 равные части, дугой показать 3\4).
- Что узнаем сначала?
(Сколько метров в одной части, если в 3частях 12метров).
- Каким действием?
(Делением)
- Что узнаем затем?
(Сколько метров вся лента, если одна часть 4 метра, а всего частей 4).
- Каким действием?
(Умножением 4*4=16м).
Подвести детей к выводам:
1 .Чтобы найти дробь числа, надо число разделить на знаменатель, а потом умножить на числитель.
2. Чтобы найти число по его дроби, надо число разделить на числитель и умножить
на знаменатель.
Задание. Приведите пример задачи и выполните решение с разбором.
Для закрепления полученных знаний предлагаются упражнения, например:
а) поставь вместо квадратов числа, чтобы равенства были верны: 1/2= /4; 2/4= /8; 3/4= /8;
б) используя рисунок, сравни дроби: 3/5 и 4/5; 6/10 и 3/5; 1и5/5;
в) сколько минут в 1/3 ч., в 1/6 ч., в 1/10 ч.
Методика изучения элементов геометрии.
Геометрический материал, изучаемый в начальной школе, не выделяется в программе в качестве самостоятельного раздела. Его изучение равномерно распределено по всему курсу математики и связанно с изучением алгебраического и арифметического материала. В целом геометрический материал представляет собой содержание подготовительной части курса геометрии, является базой для изучения систематического курса геометрии. Основными задачами его изучения являются следующие:
Сформировать у учащихся четкие представления об основных геометрических фигурах и геометрических телах, привить им элементарные навыки определения простейших геометрических понятий, навыков четкой формулировки выводов на основе наблюдений.
Формировать практические умения и навыки в выполнении построений с помощью основных инструментов; измерения геометрических величин.
Развивать логическое мышление учащихся, пространственные представления.
В начальной школе изучается следующий основной геометрический материал:
Точка. Линии. Виды линий: прямая, кривая, ломанная; звено ломаной линии, замкнутые и незамкнутые ломаные линии. Длина ломаной.
Луч. Его отличие от прямой.
Отрезок. Построение прямых линий, лучей и отрезков; обозначение отрезков при помощи букв; сравнение длин отрезков приложением и наложением; построение отрезков при помощи линейки.
Угол. Виды углов ( прямой, острый, тупой); построение углов, обозначение углов буквами.
Многоугольники: их классификация по количеству углов; обозначение многоугольников при помощи букв. Углы, вершины, стороны многоугольников.
Прямоугольник и его свойства; квадрат, как особый прямоугольник. Построение прямоугольника, квадрата на бумаге. Диагонали прямоугольника. Свойства диагонали прямоугольника (квадрата).
Виды прямоугольников: разносторонние, равнобедренные (равносторонние); прямоугольные, остроугольные, тупоугольные.
Круг. Окружность. Центр, радиус, диаметр окружности (круга).
Понятие о периметре, площади многоугольника; нахождение периметра и площади прямоугольника, многоугольника, квадрата.
Симметричные фигуры. Ось симметрии. Построение симметричных фигур. Знакомство с геометрическими телами.
11. Куб. Его изображение. Грани вершины, ребра куба.
Прямоугольный параллелепипед. Цилиндр. Конус.
Особенность изучения данного раздела заключается в том, что свойства, признаки фигур учащиеся выявляют экспериментально, через практические работы, организацию наблюдений над геометрическими объектами (моделями фигур и их изображений).
Формирование геометрических представлений состоит из следующих этапов:
Выяснение и уточнение имеющихся у детей знаний и представлений о геометрических фигурах.
Первичное знакомство с геометрической фигурой на основе наблюдений и практических работ.
У учащихся сформирована способность к восприятию формы. Это способность позволяет узнавать, различать, изображать геометрические фигуры. Для этого достаточно показать фигуру и назвать ее соответствующим термином. Такое знакомство с фигурами позволяет детям воспринимать их как целостный образ, поэтому, если применить расположение или размер фигур, которые были предложены в образце, могут быть допущены ошибки.
3. Выделение тех элементов, из которых состоит фигура и их существенных признаков.
Несущественными называются признаки, от которых не зависит форма фигуры (материал, цвет, размер, расположение на плоскости).
Существенными называются признаки, которые определяют форму фигуры.
Существенным является число элементов, из которых она состоит (число углов, сторон, вершин). Из всех геометрических понятий, изучаемых в начальной школе, определяемыми являются понятия прямоугольника и квадрата. По свойству "все углы прямые" в множестве четырехугольников дети выделяют прямоугольники (квадраты), На основе этого свойства все четырехугольники можно разбить на две группы: прямоугольников и фигур, не являющихся прямоугольниками.
Учащиеся самостоятельно выделяют свойства некоторых прямоугольников - "имеют стороны одинаковой длины". Это свойство устанавливается путем измерения и позволяет разбить множество прямоугольников на два подмножества: квадратов и прямоугольников, не являющихся квадратами. Из множества геометрических фигур ученики выделяют квадрат с помощью трех свойств: "быть четырехугольником", "иметь четыре прямых угла", "иметь равные стороны". Из множества четырехугольников квадрат выделяется по двум свойствам: "иметь четыре прямых угла", "иметь равные стороны".
Конструирование и моделирование фигуры из определенного количества полосок бумаги, проволоки, пластилина, палочек.
Распознавание новой фигуры в окружающих предметах, в составе сложной фигуры.
Разбиение множества геометрических фигур на группы. Классификация фигур.
Построение простейших геометрических фигур на клетчатой бумаге. Процесс решения задач на построение разбивается обычно на четыре этапа: анализ, построение, доказательство, исследование. В зависимости от содержания и целей, поставленных при их решении, в начале обучения число этапов можно варьировать: построение и исследование; построение и доказательство, анализ и построение. Затем число этапов можно увеличить. Например, анализ, построение и исследование проводят при решении таких задач: «Построй прямоугольник, сумма длин сторон которого 12 см. Построй разные прямоугольники с такой же суммой длин сторон».
Анализ. Учитель предлагает подобрать числа, которые могли бы быть длинами сторон искомого прямоугольника.
Построение. По данным, полученным при анализе длин сторон искомого прямоугольника, строится один из них.
Исследование. Учащиеся устанавливают. что существуют три различных прямоугольника, сумма длин сторон которого равна 12 см : 1см и 5см , 2м и 4см, З см и Зсм. Один из прямоугольников квадрат.
Упражнения в измерении.
Распознавание новой фигуры из совокупности фигур по существенным признакам.
10. Формирование элементарных навыков чтения геометрических чертежей с использованием буквенных обозначений.
Формирование навыков определения периметра, площади фигур, величины угла.
Знакомство с отдельными геометрическими телами.
Такой подход позволяет от умения видеть отдельные предметы, выделяя в них. различные признаки переходить к сравнению предметов, группировать предметы по общим признакам, делать выводы на основе наблюдений.
Геометрические фигуры изучают в определенной последовательности, выполняя с моделями различные практические действия.
Элементарная геометрическая фигура-точка. Любую другую фигуру можно рассматривать как множество точек.
В процессе различных упражнений различают понятия «точка пересечений двух линий», «линия проходит через точку», «линия соединяет 2 точки».
В геометрии прямая линия (линия, неограниченная с обеих сторон, которую можно продолжать бесконечно долго в обе стороны) называется просто «прямая».
Часть прямой линии, ограниченная с обоих концов точками начала и конца, называется отрезком. Прямую можно обозначить любой маленькой латинской буквой или 2-мя большими латинскими буквами, не отмечая их на прямой точками.
Линия может быть «прямая» и «кривая». Кривые линии могут быть замкнутые и незамкнутые.
Если из данной точки провести по линейке прямую линию, то получим геометрическую фигуру, называемую лучом.
Если провести 2 луча из одной точки то получим геометрическую фигуру, называемую углом. В этом случае угол рассматривается как фигура, которая состоит из 2-х лучей с общим началом. Дальнейшая деятельность связана с определением угла как части плоскости, ограниченной двумя лучами.
В начальных классах дети не знакомятся с единицей измерения углов. Поэтому для формирования представлений о величине угла можно воспользоваться только приёмом наложения и представлениями об угле.
Тупой угол можно ввести как угол больше прямого, острый как угол меньше прямого.
Или, если наложить модель прямого угла на углы четырехугольника, то в этом случае:
а) одна сторона прямого угла совпадает со стороной четырехугольника, другая пройдет внутри. Это значит, что данный угол четырехугольника тупой.
Если одна сторона прямого угла совпадает со стороной четырехугольника, другая пройдет вне, это значит, что угол четырехугольника острый.
Имея представление о точке, отрезке и угле, школьники могут находить эти геометрические фигуры в треугольниках, четырехугольниках, прямоугольниках и квадратах, выделяя в качестве их элементов вершины (точки), стороны (отрезки) и углы.
Ориентируясь на эти элементы, дети могут распознавать треугольники, четырехугольники и т.д., называя все эти фигуры многоугольниками. Для упражнений в распознавании многоугольников можно применять (в некоторых программах) не только плоские фигуры, но и объемные тела - призмы, пирамиды. Оперируя с объемными телами усваиваются такие термины, как грань (многоугольник), ребро (отрезок), вершины (точка).
Если конец одного отрезка является началом другого, конец второго -началом третьего и эти отрезки образуют между собой угол, то мы видим ломаную линию, которая может быть так же, как и кривая, незамкнутой и замкнутой (многоугольник).
Треугольник - это многоугольник с тремя сторонами. Треугольник - геометрическая фигура, состоящая из трех замкнутых отрезков или трех углов, имеющих попарно совпадающие стороны.
По видам углов треугольники бывают: остроугольные, прямоугольные, тупоугольные.
У остроугольного треугольника все углы острые.
У прямоугольного - один угол прямой и два острых.
У тупоугольного треугольника: один угол тупой, два острых.
По видам сторон треугольники бывают разносторонние (все три стороны разной длины), равнобедренные (две стороны равны между собой и не равны третьей стороне), равносторонние (все стороны равны между собой).
Изучение геометрического материала проводится через систему заданий, предусмотренных программой каждого года обучения. Эта система представляет собой следующие задания:
где геометрическая фигура используется как объекты для пересчитывания; усваивается необходимая терминология, формируются умения узнавать и различать фигуры;
на сравнение геометрических фигур (на основе умения выделять способствующие формированию понятия об общих и отличительных свойствах);
на выяснение геометрической формы предметов;
выбор сходных фигур;
на классификацию фигур;
б) на преобразование;
на элементарное построение фигур на клетчатой бумаге с помощью чертежных инструментов;
на элементарное построение фигур с заданными параметрами;
на составление геометрических фигур;
на нахождение геометрических фигур на чертеже;
вычислительные, связанные с нахождением периметра, площади, объема.
Таким образом, изучаемый в начальной школе геометрический материал, дает возможность учащимся познакомиться с основными элементами геометрии, формировать умения и навыки, связанные с применением чертежных и измерительных инструментов, изучать терминологию и символику графических обозначений, развивать математическую речь.
Методика изучения элементов алгебры
В курсе математики начальной школы учащиеся знакомятся с тремя основными группами алгебраического материала:
выражения (числовые и буквенные);
равенства и неравенства;
уравнения.
В математике под выражением понимают построенную по определенным правилам последовательность математических символов, обозначающих числа и действия над ними.
Выражения вида 7+4; (5+3)+10 - называют числовыми: 8-я; 50:с - буквенными или выражениями с переменной.
В методике ознакомления учащихся с понятием числового выражения можно выделить три этапа:
Iэтап. Выражения, содержащие одно арифметическое действие: 5+2; 6-4 (1 кл) 3x2; 15:5 (2 кл).
II этап. Выражения, содержащие два или больше арифметических действий одной ступени:
4+5-3 8:2x3
10-(3+4)(1 кл) 3x2x4 (2 кл)
III этап. Выражения, содержащие два и больше арифметических действий разных ступеней:
6x3+10; 4x8+16:2
Термины "выражение", "значение выражения" вводятся во 2 классе.
Выражения, содержащие несколько действий, впервые могут появиться только со скобками. Сложные выражения получаются тогда, когда вместо одного или обоих чисел, входящих в простое выражение, берут выражение, но при этом данное выражение обязательно заключают в скобки.
Понимание учащимися принципов составления выражения, усвоения всех случаев упрощения ведет к пониманию структуры выражений, а в дальнейшем к осознанному формулированию и применению правил выполнения действий.
Одна из основных задач изучения данной темы - познакомить учащихся с правилами порядка выполнения действий в выражениях и сформировать у них умения пользоваться ими.
Анализ правил, приведенных в учебниках математики для начальных классов, позволяет выделить те основные признаки выражений, на которые учащиеся могут ориентироваться при вычислении их значений. А именно, выражения без скобок и со скобками, содержащие только сложение и вычитание, или только умножение и деление; выражения, обладающие признаками наличия скобок и всех четырех арифметических действий.
Следует иметь в виду, что еще в 1 классе они познакомились с тем, что действие, записанное в скобках, выполняется первым. Необходимость введения этого правила обусловливалась изучением свойств арифметических действий.
Для подготовки учащихся к восприятию правил как общего способа действий при вычислении значений выражений нужно научить их анализировать различные числовые выражения с точки зрения тех признаков, на которые с ориентированно каждое правило.
В учебниках, разработанных Истоминой Н.Б., для этой цели разработаны специальные задания вида:
-Сравни выражения в каждой паре. Чем они похожи? Чем отличаются? Затем работа может быть направлена на формирование умения соотносить данное выражение с определенным правилом, которым следует руководствоваться при вычислении его значения.
При вычислении значений выражений некоторые учащиеся, правильно расставив порядок выполнения действий, допускают ошибки, связанные с выбором чисел, с которыми эти действия нужно выполнять.
Для предупреждения этой ошибки полезно использовать такой прием:
3 4 1 5 2
6


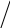 3
: 7 + (20 - 5) - (9 + б) = 9
3
: 7 + (20 - 5) - (9 + б) = 9

 9 15 15
9 15 15




 24 9
24 9
В процессе изучения данной темы учащиеся также совершенствуют вычислительные навыки. Для этой цели предлагаются упражнения на вычисление значений выражений, задания с различными способами решений, требующие от учащихся выполнения рассуждений.
Для чтения сложных выражений используют следующий алгоритм:
определяем, какое действие в выражении выполняется последним;
вспоминаем название компонентов действий;
называем, чем выражены компоненты. Формирование понятия переменной включает 3 этапа.
этап. Упражнения, раскрывающие понятие переменной, - упражнения с пропуском чисел, с "окошками".
этап. Введение букв как символов для обозначения переменной.
3 этап. Буквенная символика используется как средство обобщения
знаний о свойствах действий, взаимосвязях действий, взаимосвязях компонентов действий (по традиционной программе не используются).
Равенства и неравенства.
Равенство - это любые два числа или число и выражение, соединенные знаком равно. Равенство может быть истинным или ложным (верным или неверным). Это результат сравнения двух одинаковых чисел или выражений, имеющих одинаковое значение.
Неравенство - это результат сравнения двух неодинаковых чисел или выражений, имеющих разные математические значения.
Существуют разные способы сравнения чисел (смотри "Нумерацию чисел").
При сравнении математических выражений используется 2 способа:
1 способ. Сравнение выражений осуществляется на основе сравнения их значений. При сравнении дается памятка:
7+6 * 14-6
Найди значение математического выражения, вычислив левую часть.
Найди значение математического выражения, вычислив правую часть.
Сравни два числа.
II способ. Сравнение выражений проводится на основе знания теоретического материала. При этом детям дается установка: сравни не вычисляя. Вычисление результатов можно выполнить для проверки результата сравнения. Рассмотрим примеры:
1) 5+4 * 5-4 (сумма двух чисел всегда больше их разности) Теоретическая основа сравнения - конкретный смысл действий сложения и вычитания.
2) 8-2 * 8-3 (уменьшаемые одинаковы, вычитаемое в правой части на 1 больше, значит, разность будет на 1 меньше)
Теоретическая основа - изменение результатов в зависимости от изменения одного из компонентов.
3) 7x6= 6x7 Теоретическая основа - переместительное свойство умножения.
27x0=27x1 Теоретическая основа - правила.
8x3*8x4 8+8+8 * 8x2
Теоретическая основа - конкретный смысл действия умножения.
6) (4+2)хЗ * 4x3+2x3
Теоретическая основа - свойство действия умножения, умножение суммы на число.
Уравнение
Знакомство с уравнениями в начальной школе можно представить в виде следующей схемы;
Iчасть *+3=7 5-*=2 |
IIчасть Х+4=6 3+х=8 |
IIIчасть Х+12=45 Хх3=21 43-х=40 5хХ=40 |
IVчасть Х=312=654+79 729-х=217+163 |
*-3=5 Решение на основе знания состава числа |
Х-5=2 10-х=4 Решение- способом подбора |
х-8=32 40:х=8 35-х=20 х:4=7 Решение- на основе знания взаимосвязи между результатами и компонентами действий |
х-137=500-140 6хУ=429+120 х:18=270-50 360:х=630:7 Упрощение выражения в правой части и решение выполняется на основе знания взаимосвязей между компонентами и результатами действий |
Методика работы по обучению решению уравнений строится в 3 этапа.
I. Подготовительный этап. На этом этапе выполняются следующие виды упражнений:
решаются способом подбора примеры с пропуском числа вида: +3=7;
раскрывается связь между результатами и компонентами действий;
вводится буквенное обозначение переменной, значение буквенных выражений находят при заданных числовых значениях букв.
II Ознакомление.
В начальном курсе математики вводится уравнение как равенство, содержащее букву. Решить уравнение - значит узнать, при каких значениях буквы уравнение обращается в верное равенство. Сначала вводятся уравнения, содержащие три компонента.
Вводятся уравнения в таком порядке:
1 слагаемое;
2 слагаемое;
уменьшаемое; вычитаемое; множитель;
делимое; делитель.
Решение уравнений выполняется двумя способами: способом подбора и на основе знания взаимосвязи между результатами и компонентами действий.
Начинать необходимо со способа подбора, т.к. он формирует осознанный и математически верный подход к решению уравнений.
Ученик сразу ориентируется на то, что подобранное число надо проверить. Так, решая уравнение х+2=5, ученик пробует числа 1,2,3. Даже, если ученик сразу находит ответ, его нужно доказать.
При подборе важно определить с какого числа целесообразно начинать сравнение.
Уравнения, содержащие число в пределах 100, следует решать на основе знания взаимосвязи между результатами и компонентами действий. В процессе решения можно ввести памятку:
Прочитай уравнение.
Назови числа (компоненты).
Что известно.
Что неизвестно.
Как найти.
Реши.
Сделай проверку.
В 4 классе усложняется структура решаемых уравнений.
Даются уравнения, в которых правая часть представлена выражением (х-8=246-86)
Для того, чтобы решить уравнение, нужно преобразовать его в знакомый вид, т.е. найди значение выражения в правой части, а затем решить его на основе знания взаимосвязи. На
Это способствует формированию у детей понятий "равенство", "левая и правая части равенства». Некоторые уравнения решается на основе знания теоретического материала. Например:
99+ х=100 - знание принципа образования натуральной последовательности
292-х=200 - знание разрядного
х+20+9=829 состава чисел
35+х=35+37 - переместительное свойство сложения
Ш. Закрепление.
Даются задания творческого характера для формирования умения решать уравнения разными способами.
Несколько другой подход рассматривается по программе развивающего обучения Занкова Л.В., отраженный в учебниках, разработанных Аргинской И.И.
Впервые встречаются с уравнением в первом классе при изучении действий сложения и вычитания; в связи с необходимостью осознания связи между действиями сложения и вычитания; умножения и деления.
Даются простейшие уравнения вида: а+х=в; а-х=в; х-а=в; а-х=в- ах=в, которые решаются на основе знания взаимосвязи между результатами и компонентами действий.
Во втором классе решаются более сложные уравнения, содержащие два, три действия; решаются они на знании взаимосвязи, хотя уже здесь желательно использование других знаний.
(а+14)-7=13 (а + 14)-7 = 13
а+ 14= 13 + 7 а + (14-7) = 13
а+14 = 20 а + 7=13
А=6 а=6
Уравнение слева решается на основе знания взаимосвязи, в уравнении справа сначала применяется свойство вычитания числа из суммы, затем знание взаимосвязи.
В третьем классе цель работы меняется. Большинство заданий дается по следующему плану: предлагаются уравнение, способ которого неизвестен и
другое уравнение, в котором есть то или иное усложнение по сравнению с первым.
Основная проблема, которую нужно решить - установить, в чем заключено усложнение и найти путь преобразования, который позволит из более сложного уравнения получить более простое.
Основной способ решения уравнений на основе использования основных свойств равенств.
В соответствии с методикой, разработанной Л.Г.Петерсон, Ю.М. Колягиным, учащиеся решают уравнения на основе введения понятий "целое" и "часть".
В каждом уравнении дети находят части и целое, а затем применяют одно из правил:
целое равно сумме частей; - чтобы найти часть, надо из целого вычесть другую часть. При этом компоненты действий можно отметить на чертеже:
Х + 8=12 х-6 = 9 14-х = 5
Величины, их единицы измерения и соотношения между ними (длина, масса, время, емкость, площадь).
В величинах отражены свойства различных объектов, явлений реального мира. Так, например, свойству пространственной протяженности соответствует длина, свойству инертности - величина, называемая массой.
Понятие величины формировалось постепенно в результате абстрагирования от качественных особенностей, свойств реальных объектов, в результате чего выделились только количественные отношения. Величины - это не сама реальность, а лишь ее отображения, но они верно отражают свойства окружающей действительности.
Имеющийся у ребенка опыт позволяет осознать значимость данного понятия, связать его с реальными предметами и явлениями, перевести имеющиеся житейские понятия на язык математики. Дети встречаются с необходимостью сравнивать реальные предметы между собой по определенным признакам.
Предметы можно сравнить по размеру, цвету, форме и т.д. Среди всех характеристик реальных предметов, обладающих определенными свойствами, выделяются такие, относительно которых можно ввести отношения "больше", "меньше" (2 карандаша по длине, 2 книги - по массе неодинаковы.)
В настоящее время в математике определено несколько подходов к понятию скалярной величины: в одних случаях она определяется как функция с заданными свойствами, в других как множество с некоторой совокупностью свойств. Ни один из таких подходов не приемлем в обучении младшего школьника, так как любая аксиоматика скалярных величин обладает высоким уровнем абстракции. Задача состоит в том, чтобы выработать интуитивно понятный учащимся способ изложения, не противоречащий дальнейшим уточнениям понятия, в результате чего у детей формируется представление о величине как о некотором свойстве предметов и явлений, которое связано с измерением.
Хотя формирование представлений о каждой конкретной величине имеет свои особенности, целесообразно выделить общие этапы, которые соблюдаются при изучении каждой величины:
I. Выяснение и уточнение имеющихся представлений о данной величине. Введение понятия и знакомство с термином.
II. Сравнение однородных величин (визуально, с помощью ощущений, наложением, приложением, путем использования различных мерок).
Знакомство с единицей измерения данной величины и с измерительным прибором.
Формирование измерительных умений и навыков.
V. Сложение к вычитание однородных величин, выраженных в единицах одного наименования.
VI. Знакомство с новыми единицами измерения величины в связи с изучением нумерации по концентрам, перевод однородных величин, выраженных в единицах двух наименований , в единицы одного наименования.
VII. Сложение и вычитание величин, выраженных в единицах двух наименований.
VIII. Умножение и деление величины на число.
На примере длины отрезка на основе предметной деятельности с опорой на конкретно-чувственное восприятие представляется возможность познакомить младших школьников со свойствами, общими для большинства скалярных величин. С таких же позиций рассматриваются другие скалярные величины и их свойства.
Действия над величинами и их отношения равносильны аналогичным действиям и отношениям с их числовыми значениями.
1. Если величины а и в измерены при помощи одной и той же единицы, то отношение между ними (а и в) будут такими же, как и отношения между их числовыми значениями, и наоборот.
Например, если массы двух предметов таковы, что а= 5 кг, в= 3 кг, то а > Ь, т.е. 5 > 3.
2. Если величины а и в измерены при помощи одной и той же единицы, то, чтобы найти числовое значение суммы а + в, достаточно сложить числовые значение а и в.
Если а= 7 кг, в= 5 кг, то а+ в = 7 кг + 5 кг = 12 кг
3. Если величины aиd таковы, что d = ах, где х - неотрицательное число, то, чтобы найти числовое значение величины d, достаточно числовое значение величины а умножить на число х.
Например, если масса d в 3 раза больше массы а и а= 3 кг, той = ЗкгхЗ = 9 кг
В начальной школе можно ввести свойства отношений между величинами (термины не давать).
1. Симметричность равенства: если а = в, то в = а. Так, если длина одного отрезка равна длине второго отрезка, то н длина
второго отрезка равна длине первого отрезка.
2. Антисимметричность неравенства: если а > Ь, то Ь< а, (если одна величина, больше второй, то вторая меньше первой).
Так, если масса арбуза больше массы тыквы, то масса тыквы меньше массы арбуза.
3. Транзитивность равенства: если а = в, в = с, то а = с. Так, если площадь одной фигуры равна площади второй фигуры, а площадь
второй фигуры равна площади третьей фигуры, то площадь первой фигуры равна площади 3 фигуры.
4. Транзитивность неравенства: если а > b, b > с, то а > с.
Так, если емкость одного сосуда больше емкости второго сосуда, а емкость
второго сосуда больше емкости третьего, то емкость первого больше емкости 3. Таким образом, можно сделать следующие выводы:
Величина - это свойство предметов, которое может быть измерено и результат измерения выражен числом.
Длина, масса, емкость, время, площадь - являются величинами.
Чтобы измерить величину, надо выбрать мерку и узнать, сколько раз она содержится в измеряемой величине, т.е. сравнить с некоторой величиной того же рода, принятой чя единицу. Величины могут быть разных родов.
Если изменяется мерка, то изменяется и значение величины. Поэтому сравнивать, складывать и вычитать величины можно только тогда, когда они измерены одной и той же меркой.
Числовые значения скалярных величин получаются в результате измерения; запись числового значения величины осуществляется с указанием единицы измерения.
Ошибка - непонимание разницы между величиной и единицами измерения величины.
Например, длина - это свойство предметов, характеризующее его протяженность. Сантиметр и другие единицы измерения длины - это отрезки, которыми измеряется длина.
7. Формирование представлений о величине связанно с изучением нумерации десятичной системы счисления, с формированием представлений о числе, т.к.
1) число получаем в результате измерения (т.е один из способов образования числа);
2) усваивается структура двузначных, трехзначных и др. чисел: 12 см = 1 дм 2 см
125 дм = I м 2 дм 5 см и т.д.
3) отношения между единицами измерения так же как отношения между разрядными единицами
1 десяток = 10 единиц
1 дм -10 см и т.д.
В результате у детей формируется представление о скалярной величине как об элементе множества скалярных величин; о том, что величины эти могут быть разных родов; если они одного рода, то их можно сравнивать, складывать и вычитать, причем складывать можно в любом порядке; числовые значения скалярных величин получаются в результате измерений; запись числового значения величины осуществляется с указанием единицы измерения.
Методика работы по обучению решению уравнений строится в 3 этапа.
I. Подготовительный этап.
На этом этапе выполняются следующие виды упражнений:
решаются способом подбора примеры с пропуском числа вида : +3=7
раскрывается связь между результатами и компонентами действий
вводится буквенное обозначение переменной, значение буквенных выражений находят при заданных числовых значениях букв.
II Ознакомление.
В начальном курсе математики вводится уравнение как равенство, содержащее букву. Решить уравнение - значит узнать, при каких значениях буквы уравнение обращается в верное равенство. Сначала вводятся уравнения, содержащие три компонента.
Вводятся уравнения в таком порядке:
1 слагаемое;
2 слагаемое;
уменьшаемое;
вычитаемое;
множитель;
делимое;
делитель.
Решение уравнений выполняются двумя способами: способом подбора и на основе знания взаимосвязи между результатами и компонентами действий.
Начинать необходимо со способа подбора, т.к. он формирует осознанный и математически верный подход к решению уравнений.
Ученик сразу ориентируется на то, что подобранное число надо проверить. Так, решая уравнение х+2=5, ученик пробует числа 1,2,3.
Даже, если ученик сразу находит ответ, его нужно доказать.
При подборе важно определить с какого числа целесообразно начинать сравнение.
Уравнения, содержащие число в пределах 100, следует решать на основе знания взаимосвязи между результатами и компонентами действий.
В процессе решения можно ввести памятку:
Прочитай уравнение.
Назови числа (компоненты).
Что известно.
Что неизвестно.
Как найти.
Реши.
Сделай проверку.
В 4 классе усложняется структура решаемых уравнений.
Даются уравнения, в которых правая часть представлена выражением.
(x8=246-86)
Для того, чтобы решить уравнение, нужно преобразовать его в знакомый вид, т.е. найди значение выражение в правой части, а затем решить его на основе знания взаимосвязи.
Это способствует формированию у детей понятий "равенство", "левая и правая части равенства".
Некоторые уравнения решаются на основе знания теоретического материала.
Например:
99+х=100 - знание принципа образования натуральной последовательности.
292-х=200 знание разрядного
х+20+9=829 состава чисел
35+х=35+37 переместительное свойство сложение
III. Закрепление.
Даются задание творческого характера для формирования умения решать уравнения разными способами.
Возможны другие подходы к изучению данной темы.
Несколько другой подход рассматривается по программе развивающего обучения Занкова Л.В., отраженная в учебниках разработанных Аргинской И.И.
Впервые встречаются с уравнением в первом классе при изучении действий сложения и вычитания; в связи с необходимостью осознания связи между действиями плюс и минус; умножение и деление.
Даются простейшие уравнения вида : а+х=в; а-х=в; х-а=в; аx=в: а:х=в,
Которые решаются на основе знания взаимосвязи между результатами и компонентами действий.
Во втором классе решаются более сложные уравнения, содержащие два-три действия; решаются они на знании взаимосвязи, хотя уже здесь желательно использованием других знаний.
(а + 14) - 7 = 13 (а + 14) - 7 = 13
а + 14 = 13 + 7 а + (14 - 7) = 13
а + 14 = 20 а + 7 = 13
а = 6 а = 6
Уравнение слева решается на основе знания взаимосвязи, в уравнении справа сначала применяется свойство вычитания числа из суммы, затем знание взаимосвязи.
В третьем классе цель работы меняется. Большинство заданий дается по следующему плану: предлагаются уравнение, способ которого неизвестен и другое уравнение, в котором есть то или иное усложнение по сравнению с первым.
Основная проблема, которую нужно решить – установить, в чем заключено усложнение и найти путь преобразования, который позволит из более сложного уравнения получить более простое.
Основной способ решения уравнений на основе использования основных свойств равенств.
В соответствии с методикой, разработанной Л.Г.Петерсон, Ю.М. Колягиным, учащиеся решают уравнения на основе введения понятий "целое" и "часть".
В каждом уравнении дети находят части и целое, а затем применяют одно из правил:
целое равно сумме частей;
чтобы найти часть, надо из целого вычесть другую часть.
При этом компоненты действий можно отметить на чертеже:
Х + 8 =12 х - 6 = 9 14 - х = 5





Х 8 6 9 х 5
Х=12 - 8 х= 6 + 9 х = 14 - 5
Х = 4 х = 15 х = 9
Величины, их единицы измерения и соотношения между ними (длина, масса, время, емкость, площадь).
В величинах отражены свойства различных объектов, явлений реального мира. Так, например, свойству пространственной протяженности соответствует длина, свойству инертности - величина, называемая массой.
Понятие величины формировалось постепенно в результате абстрагирования от качественных особенностей, свойств реальных объектов, в результате чего выделились только количественные отношения. Величины - это не сама реальность, а лишь ее отображения, но они верно отражают свойства окружающей действительности.
Имеющийся у ребенка опыт позволяет осознать значимость данного понятия, связать его с реальными предметами и явлениями, перевести имеющиеся житейские понятия на язык математики. Дети встречаются с необходимостью сравнивать реальные предметы между собой по определенным признакам.
Предметы можно сравнить по размеру, цвету, форме и т.д. Среди всех характеристик реальных предметов, обладающих определенными свойствами, выделяются такие, относительно которых можно ввести отношения "больше", "меньше" (2 карандаша по длине, 2 книги - по массе неодинаковы.)
В настоящее время в математике определено несколько подходов к понятию скалярной величины: в одних случаях она определяется как функция с заданными свойствами, в других как множество с некоторой совокупностью свойств. Ни один из таких подходов не приемлем в обучении младшего школьника, так как любая аксиоматика скалярных величин обладает высоким уровнем абстракции. Задача состоит в том, чтобы выработать интуитивно понятный учащимся способ изложения, не противоречащий дальнейшим уточнениям понятия, в результате чего у детей формируется представление о величине как о некотором свойстве предметов и явлений, которое связано с измерением.
Хотя формирование представлений о каждой конкретной величине имеет свои особенности, целесообразно выделить общие этапы, которые соблюдаются при изучении каждой величины:
I. Выяснение и уточнение имеющихся представлений о данной величине. Введение понятия и знакомство с термином.
II. Сравнение однородных величин (визуально, с помощью ощущений, наложением, приложением, путем использования различных мерок).
III. Знакомство с единицей измерения данной величины и с измерительным прибором.
IV. Формирование измерительных умений и навыков.
V. Сложение и вычитание однородных величин, выраженных в единицах одного наименования.
VI. Знакомство с новыми единицами измерения величины в связи с изучением нумерации по концентрам, перевод однородных величин, выраженных в единицах двух наименований , в единицы одного наименования.
VII. Сложение и вычитание величин, выраженных в единицах двух наименований.
VIII. Умножение и деление величины на число.
На примере длины отрезка на основе предметной деятельности с опорой на конкретно-чувственное восприятие представляется возможность познакомить младших школьников со свойствами, общими для большинства скалярных величин. С таких же позиций рассматриваются другие скалярные величины и их свойства.
Действия над величинами и их отношения равносильны аналогичным действиям и отношениям с их числовыми значениями.
Если величины а и в измерены при помощи одной и той же единицы, то отношение между ними (а и в) будут такими же, как и отношения между их числовыми значениями, и наоборот.
Например, если массы двух предметов таковы, что а= 5 кг, в= 3 кг, то
а > b, т.е. 5 > 3.
Если величины а и в измерены при помощи одной и той же единицы, то, чтобы найти числовое значение суммы а + в, достаточно сложить числовые значение а и в.
Если а= 7 кг, в= 5 кг, то а + в = 7 кг + 5 кг = 12 кг
Если величины а и d таковы, что d = ах, где х - неотрицательное число, то, чтобы найти числовое значение величины d, достаточно числовое значение величины а умножить на число х.
Например, если масса d в 3 раза больше массы а и а= 3 кг, то d = 3 кг х 3 = 9 кг
В начальной школе можно ввести свойства отношений между величинами (термины не давать).
Симметричность равенства: если а = в, то в = а.
Так, если длина одного отрезка равна длине второго отрезка, то и длина второго отрезка равна длине первого отрезка.
Антисимметричность неравенства: если а > b, то b< а, (если одна величина, больше второй, то вторая меньше первой).
Так, если масса арбуза больше массы тыквы, то масса тыквы меньше массы арбуза.
Транзитивность равенства: если а = в, в = с, то а = с.
Так, если площадь одной фигуры равна площади второй фигуры, а площадь второй фигуры равна площади третьей фигуры, то площадь первой фигуры равна площади 3 фигуры.
Транзитивность неравенства: если а > b, b > c, то а > с.
Так, если емкость одного сосуда больше емкости второго сосуда, а емкость второго сосуда больше емкости третьего, то емкость первого больше емкости 3.
Таким образом, можно сделать следующие выводы:
Величина - это свойство предметов, которое может быть измерено и результат измерения выражен числом.
Длина, масса, емкость, время, площадь - являются величинами.
Чтобы измерить величину, надо выбрать мерку и узнать, сколько раз она содержится в измеряемой величине, т.е. сравнить с некоторой величиной того же рода, принятой за единицу. Величины могут быть разных родов.
Если изменяется мерка, то изменяется и значение величины. Поэтому сравнивать, складывать и вычитать величины можно только тогда, когда они измерены одной и той же меркой.
Числовые значения скалярных величин получаются в результате измерения; запись числового значения величины осуществляется с указанием единицы измерения.
Ошибка - непонимание разницы между величиной и единицами измерения величины.
Например, длина - это свойство предметов, характеризующее его протяженность. Сантиметр и другие единицы измерения длины - это отрезки, которыми измеряется длина.
7. Формирование представлений о величине связанно с изучением
нумерации десятичной системы счисления, с формированием
представлений о числе, т.к.
число получаем в результате измерения (т.е один из способов образования числа);
усваивается структура двузначных, трехзначных и др. чисел:
12 см = 1 дм 2 см
125 дм = 1 м 2 дм 5 см и т.д.
отношения между единицами измерения так же как отношения между разрядными единицами
1 десяток = 10 единиц
1 дм - 10 см и т.д.
В результате у детей формируется представление о скалярной величине как об элементе множества скалярных величин; о том, что величины эти могут быть разных родов; если они одного рода, то их можно сравнивать, складывать и вычитать, причем складывать можно в любом порядке; числовые значения скалярных величин получаются в результате измерений; запись числового значения величины осуществляется с указанием единицы измерения.
