
- •1. Предмет теории вероятностей. Исходные понятия теории вероятностей (вероятность, испытание, событие, совместные и несовместные события).
- •2. Классификация событий (достоверные, невозможные и случайные события).
- •3. Классическое, статистическое и геометрические определения вероятности.
- •4. Элементы комбинаторики (размещения, перестановки, сочетания).
- •5. Теорема сложения вероятностей несовместных и совместных событий.
- •6. Элементарные события, полная группа событий. Противоположные события, вероятность противоположных событий.
- •7. Независимые события, умножение вероятностей независимых событий. Вероятность появления хотя бы одного события
- •8. Зависимые события, условная вероятность, умножение вероятностей зависимых событий.
- •9. Формула полной вероятности, формулы Байеса.
- •Формула Бейеса (Байеса)
- •10. Повторные испытания. Схема Бернулли.
- •11. Формула Пуассона для повторных испытаний.
- •12. Понятие случайной величины, дискретная и непрерывная случайные величины. Закон распределения вероятностей дискретной случайной величины, способы его задания.
- •13. Законы распределения дискретной случайной величины: биномиальный и Пуассона.
- •14. Статистические характеристики дискретной случайной величины.
- •15. Свойства математического ожидания дискретной случайной величины.
- •16. Свойства дисперсии дискретной случайной величины, основные формулы.
- •Свойства функции распределения вероятностей случайной величины
- •18. Функция распределения плотности вероятностей непрерывной случайной величины, ее числовые характеристики мат. Ожидание, дисперсия, среднее квадратичное отклонение.
- •19. Вероятность попадания значения непрерывной случайной в заданный интервал.
- •20. Равномерное распределение плотности вероятности непрерывной случайной величины.
- •22. Вероятность попадания значений непрерывной случайной величины в заданный интервал для нормального распределения плотности вероятностей.
- •23. Расчет вероятности заданного отклонения нормальной случайной величины. Правило трех сигм.
- •Правило трех сигм
- •26. Понятия генеральной совокупности, выборки и степени ее свободы, связных и несвязных выборок, нулевой и альтернативной гипотез.
- •Зависимые(связанные) и независимые (несвязанные) выборки
- •28. Непараметрические критерии, критерии знаков и Вилкоксона, их сходство и различия.
- •Алгоритм подсчета g – критерия знаков.
- •29. Параметрические критерии Стьюдента и Фишера, их сходство и различия.
- •30. Критерий согласия χ 2- Пирсона, его особенности и процедура принятия статист. Вывода.
Свойства функции распределения вероятностей случайной величины
1. Значения
функции распределения вероятностей
принадлежат отрезку ![]() :
:
![]() .
2. Функция
распределения вероятностей – неубывающая
функция, то есть:
.
2. Функция
распределения вероятностей – неубывающая
функция, то есть:
![]() ,
если
,
если ![]() .
Следствие
1. Вероятность
того, что случайная величина примет
значение, заключенное в интервале
.
Следствие
1. Вероятность
того, что случайная величина примет
значение, заключенное в интервале ![]() ,
равна приращению функции распределения
вероятностей на этом интервале:
,
равна приращению функции распределения
вероятностей на этом интервале:
![]() .
Следствие
2. Вероятность
того, что непрерывная случайная величина
примет одно определенное значение,
равна нулю.
Используя последнее
следствие, легко убедиться в справедливости
следующих равенств:
.
Следствие
2. Вероятность
того, что непрерывная случайная величина
примет одно определенное значение,
равна нулю.
Используя последнее
следствие, легко убедиться в справедливости
следующих равенств:
![]() .
3. Если
возможные значения непрерывной случайной
величины принадлежат интервалу
,
то:
.
3. Если
возможные значения непрерывной случайной
величины принадлежат интервалу
,
то:
![]() ,
если
,
если ![]() ;
;
![]() ,
если
,
если ![]() .
Следствие. Если
возможные значения непрерывной случайной
величины расположены на всей числовой
оси, то справедливы следующие предельные
соотношения:
.
Следствие. Если
возможные значения непрерывной случайной
величины расположены на всей числовой
оси, то справедливы следующие предельные
соотношения:
![]() ;
;
![]() .
График
.
График
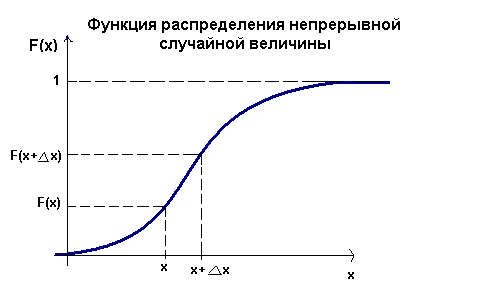
18. Функция распределения плотности вероятностей непрерывной случайной величины, ее числовые характеристики мат. Ожидание, дисперсия, среднее квадратичное отклонение.
Плотностью
распределения вероятностей непрерывной
случайной величины
называют
функцию ![]() –
первую производную от функции
распределения вероятностей
:
–
первую производную от функции
распределения вероятностей
:
![]() .
Таким
образом, функция распределения
вероятностей является первообразной
для плотности распределения
вероятностей.
Теорема. Вероятность
того, что непрерывная случайная
величина
примет
значение, принадлежащее интервалу
,
равна определенному интегралу от
плотности распределения, взятому в
соответствующих пределах:
.
Таким
образом, функция распределения
вероятностей является первообразной
для плотности распределения
вероятностей.
Теорема. Вероятность
того, что непрерывная случайная
величина
примет
значение, принадлежащее интервалу
,
равна определенному интегралу от
плотности распределения, взятому в
соответствующих пределах:
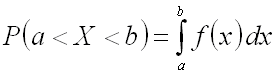 .
Следовательно,
зная плотность распределения
вероятности
,
можно найти функцию распределения
по
формуле
.
Следовательно,
зная плотность распределения
вероятности
,
можно найти функцию распределения
по
формуле
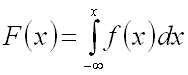 .
.
Свойства плотности распределения вероятностей
1. Плотность
распределения вероятностей –
неотрицательная функция:
![]() .
2. Несобственный
интеграл от плотности распределения
вероятностей в пределах от
.
2. Несобственный
интеграл от плотности распределения
вероятностей в пределах от ![]() до
до ![]() равен
единице:
равен
единице:
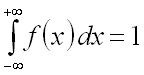 .
.
Вероятностный
смысл плотности распределения
вероятности. Вероятность
того, что непрерывная случайная величина
примет значение, принадлежащее
интервалу ![]() ,
приближенно равна (с точностью до
бесконечно малых высшего порядка
относительно
,
приближенно равна (с точностью до
бесконечно малых высшего порядка
относительно ![]() )
произведению плотности распределения
вероятности в точке на длину интервала
:
)
произведению плотности распределения
вероятности в точке на длину интервала
:
![]() .
.
Числовые характеристики непрерывных случайных величин
Математическим
ожиданием непрерывной случайной
величины
,
возможные значения которой принадлежат
отрезку ![]() ,
называют определенный интеграл
,
называют определенный интеграл
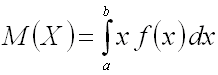 .
Если
возможные значения принадлежат всей
числовой оси, то
.
Если
возможные значения принадлежат всей
числовой оси, то
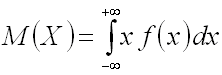 (предполагается,
что несобственный интеграл, стоящий в
правой части равенства, существует).
Дисперсией
непрерывной случайной величины называют
математическое ожидание квадрата ее
отклонения.
Если возможные непрерывной
случайной величины
принадлежат
отрезку
,
то
(предполагается,
что несобственный интеграл, стоящий в
правой части равенства, существует).
Дисперсией
непрерывной случайной величины называют
математическое ожидание квадрата ее
отклонения.
Если возможные непрерывной
случайной величины
принадлежат
отрезку
,
то
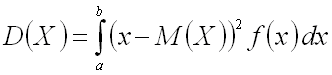 .
Если
возможные значения принадлежат всей
числовой оси, то
.
Если
возможные значения принадлежат всей
числовой оси, то
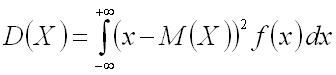 (предполагается,
что несобственный интеграл, стоящий в
правой части равенства, существует).
Средним
квадратическим отклонением непрерывной
случайной величины называют,
как и для величины дискретной, квадратный
корень из дисперсии:
(предполагается,
что несобственный интеграл, стоящий в
правой части равенства, существует).
Средним
квадратическим отклонением непрерывной
случайной величины называют,
как и для величины дискретной, квадратный
корень из дисперсии:
![]() .
.
