17.2. Поиск минимума функции нескольких переменных

Минимум функции нескольких переменных может быть найден численными методами на компьютере. Существуют алгоритмы такого поиска. Например, известный алгоритм градиентного спуска. Рассмотрим метод прямого поиска минимума функции нескольких переменных. Существует стандартная процедура- DIRECTSEARCH такого поиска. Как построен алгоритм? Рассмотрим рис.18

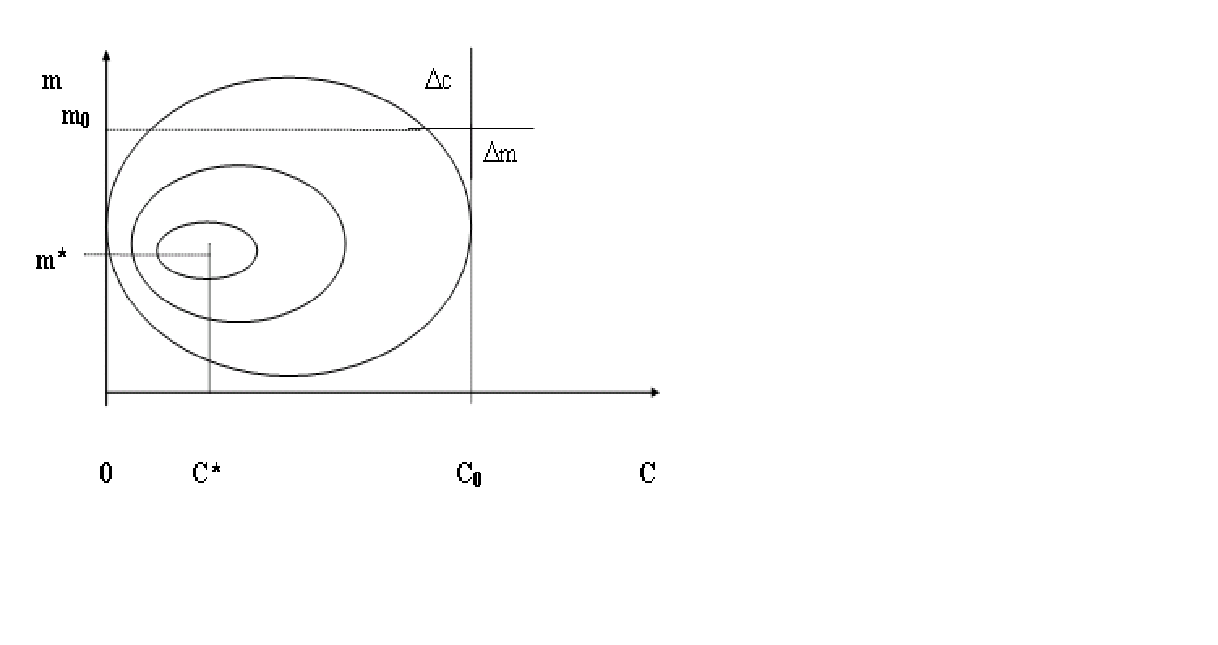
Рис.18.

На рисунке 18 изображены изолинии функции σ(c,m)=const. Выберем произвольную начальную точку m₀, c₀. У нас есть алгоритм (формула), позволяющая вычислить функцию σ(c,m). Вычислим значение этой функции в начальной точке. Зададим некоторый шаг c, m и вычислим значения σ (c,m) ещё в четырёх точках: σ(c₀,m₀+m), σ(c₀,m₀ -m), σ(c₀+c,m₀), σ(c₀ -c,m₀), то есть, определим значения функции σ для некоторой расстановки типа крест. Затем выберем из этих значений минимальное. В данном случае это будет σ(c₀, m₀ - c) и переместим центр расстановки в эту точку. Далее процедура вычислений повторяется. Крест будет ползти в сторону минимума. Если минимальное значение получается в центральной точке креста - шаг дробится. Алгоритм процедуры прямого поиска становится понятнее, если рассмотреть обращение к процедуре DIRECTSEARCH.

DIRECTSEARCH (N(число переменных), RHO(параметр уменьшения шага поиска), DL(наименьший шаг), MF(процедура вычисления значений функции), M(максимальное число вычислений функции), MX(начальный шаг), D(координаты минимума), MFS(значение функции в точке минимума), P₁ (логическая переменная, если P₁ - истинно, то найден минимум, если P₁ - ложно выход из процедуры осуществлён при достижении количества вычислений функции больше значения M).

Структура линий уровня функции σ нам не известна - функция может содержать несколько минимумов. Эта проблема решается следующим образом: задаём несколько значений начальных точек, в нашем случае - 4. Вычислим координаты четырёх точек минимума. А затем выберем из них ту, в которой значение σ наименьшее.

В рассмотренном случае, мы считаем функцию σ функцией двух переменных. Однако, как мы сейчас увидим, эта задача может быть сведена к поиску функции одной переменной. Действительно, если для пары годографов, задано некоторое произвольное значение параметра С, то оптимальное значение m степени однородной аппроксимирующей функции может быть вычислено. Возьмём произвольную точку прямого годографа х₁, t₁. Зададим некоторое значение С. Соответствующая точка х₂ (образ точки х₁) , при заданном значении С может быть найдена по формуле:

Возьмём значение t₂ в точке x₂. Известно, что:

отсюда:

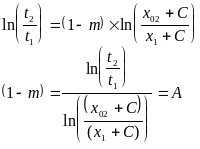
m = 1 - A

Взяв несколько точек прямого годографа вычислим , для каждой пары точек можно вычислить своё значение m_i, а затем вычислить среднеарифметическое значение:

После этого для заданного С и вычисленного m необходимо найти среднеквадратическое отклонение прямого наблюдённого от преобразованного прямого σ (С, m). В этом случае σ является функцией только одного переменного С. Таким образом можно вести поиск минимума функции σ (С) передвигаясь только по одной координате С. Это уменьшает время счёта примерно в пять раз. Точность вычислений при этом не теряется. Итак, минимум найден. Пусть это будут значения m^*, C^*.