Введение
Электрическая цепь включает резистивные (R,G) и динамические (L,C) пассивные элементы, а также источники энергии: независимые источники напряжения E и тока J, управляемые источники напряжения ИНУН, ИНУТ и тока ИТУН, ИТУТ. Соединение элементов рассматривается как обобщенная электрическая ветвь и ее частные случаи (рис. 1).
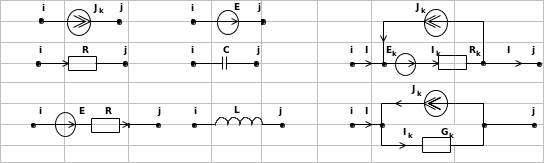
Рис. 1
Д
ля
каждого элемента схемы можно на основании
законов Ома и Кирхгофа записать уравнения
электрического равновесия:
- резистивный элемент R
,
,
,
j-
i+
;
- индуктивный элемент L
,
,
,
- емкостной элемент C
,
,
,
-
короткозамкнутая ветвь
i-
j=
,
- источник тока I =J,
- источник напряжения
i-
j+
=
,
- обобщенная ветвь
,
— R-
ветвь
i-
j=
,
— G-
ветвь
i-
j)
.
Все эти уравнения можно рассматривать как математические модели линейных элементов – двухполюсников.
Состояние электрической цепи зависит не только от элементов схемы, но и от способа их соединения. Для узлов и контуров схемы записывают уравнения электрического равновесия на основании законов Кирхгофа. Они выражают связь между напряжениями и токами ветвей и называются топологическими.
Для сложных электрических цепей, состоящих из большого числа линейных двухполюсников, целесообразно перейти от электрической цепи (рис. 2) к графу (рис. 3). При этом узлы (место соединения трёх и более ветвей) схемы соответствуют вершинам графа, а её ветви – его рёбрам.
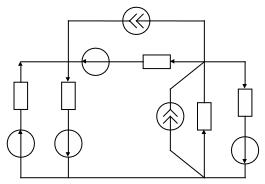
J3
1 E3 R3 IR3 2
IR1 IR2 IR5
R1 R2
R5
J4 R4
E1 E2 IR4
E5
3
Рис. 2
Ветви, содержащие идеальные источники тока, на графе не показывают, так как по определению они имеют бесконечно большое сопротивление.
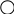1
3 2
1 2 4 5
3
Рис. 3
Такой граф называется ориентированным (направленным) графом. Каждая ветвь его рассматривается как обобщённая электрическая ветвь (рис. 4), для которой справедлив закон Ома в матричной форме записи
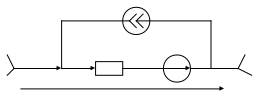J
I IR R E
U
Рис. 4
U = R(I + J) – E,
I = G(U + E) – J,
где U – вектор – столбец напряжений обобщённых ветвей размерностью b×1, b – число обобщённых ветвей; R и J – диагональные матрицы сопротивлений и проводимостей ветвей размерностью b×1; I – вектор – столбец токов обобщённых ветвей размерностью b×1; J – вектор – столбец токов источников токов размерностью b×1; E – вектор – столбец ЭДС источников напряжения размерностью b×1.
Формализованный переход от графической модели к математической реализуется в виде матрицы инциденций А размерностью (q-1)×b, у которой строки соответствуют узлам, а столбцы – ветвям. Здесь q – число вершин графа, b – число его дуг. Элементы этой матрицы имеют значения +1, -1 и 0, если дуга выходит из вершины, входит в вершину и не связана с этой вершиной.
Тогда первое уравнение Кирхгофа можно представить в виде
AI = 0.
Получить независимую систему уравнений второго закона Кирхгофа можно при помощи дерева графа схемы (на рис. 3 это выделенные ветви 1 и 5). Дерево содержит все узлы графа, но ни одного контура, и ветви связи, дополняющие до исходного графа. Число ветвей дерева d = q – 1, число ветвей связи k = b – (q - 1). Ветви связи 2, 3, 4 образуют главные контуры, направление обхода контура определяется направлением ветви связи.
Тогда второе уравнение Кирхгофа в матричной форме имеет вид
BU = 0,
где В – матрица главных контуров размерностью k × b, т.е. строки соответствуют контурам, а столбцы – ветвям. Элементы этой матрицы имеют значения +1, если ветвь входит в контур и её направление совпадает с направлением обхода контура; -1, если не совпадает; 0, если ветвь не содержится в контуре.
Если в качестве неизвестных выбрать потенциалы независимых узлов (например, φ1 и φ2), то необходимо решать матричное уравнение
AGATφ = AJ – AJE, (1)
где G – диагональная матрица проводимостей ветвей.
Если в качестве неизвестных выбрать контурные токи (токи ветвей связи), то необходимо решать матричное уравнение
BRBTI = BE – BRJ. (2)
Токи ветвей связаны с контурными токами соотношением Ib = BTI.
Для схемы рис. 2 (φ3 = 0; дерево графа ветви 1 и 5; ветви связи – 2, 3, 4; главные контуры – ветви 2 и 1; 3, 1 и 5; 4 и 5) матрицы, входящие в эти уравнения, имеют вид
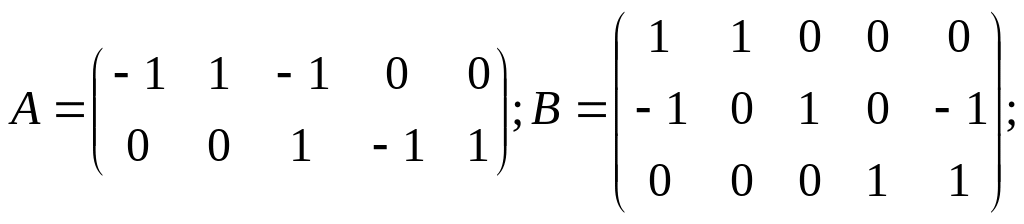
Пусть Е1 = 3 В, Е2 = Е3 = 2 В, Е5 = 1 В; J3 = 1 A, J4 = 0,5 A;
R1 = 4 Ом, R2 = 6 Ом, R3 = 2 Ом, R4 = 8 Ом, R5 = 10 Ом.
Рассмотрим решение матричных уравнений (1) и (2) в среде MATLAB.
>> A=[-1 1 -1 0 0;0 0 1 -1 1]
A =
-1 1 -1 0 0 - матрица соединений
0 0 1 -1 1
>> B=[1 1 0 0 0;-1 0 1 0 -1;0 0 0 1 1]
B =
1 1 0 0 0
-1 0 1 0 -1 - матрица главных контуров
0 0 0 1 1
>> RB=[4 6 2 8 10]
RB =
4 6 2 8 10 - матрица сопротивлений ветвей
>> R=diag(RB)
R =
4 0 0 0 0
0 6 0 0 0 - диагональная матрица сопротивлений
0 0 2 0 0
0 0 0 8 0
0 0 0 0 10
>> RK=B*R*B'
RK =
10 -4 0
-4 16 -10 - матрица контурных сопротивлений
0 -10 18
>> E=[3;2;2;0;1]
E =
3
2 - матрица ЭДС ветвей
2
0
1
>> J=[0;0;-1;-0.5;0]
J =
0
0 - матрица источников токов
-1.0000
-0.5000
0
>> EK=B*E-B*R*J
EK =
5 - матрица контурных ЭДС
0
5
>> IB=RK^(-1)*EK - токи ветвей связи
IB =
0.7161 ток I2
0.5402 ток I3
0.5779 ток I4
>> IB=RK\EK - токи ветвей связи
IB =
0.7161
0.5402
0.5779
>> IB=inv(RK)*EK - токи ветвей связи
IB =
0.7161
0.5402
0.5779
>> I=B'*IB - токи обобщённых ветвей
I =
0.1759 ток I1
0.7161
0.5402
0.5779
0.0377 ток I5
Токи сопротивлений рассчитываются по формулам:
IR1 = I2 – I3 = 0,716 – 0,540 = 0,156 A;
IR2 = I2 = 0,716 A;
IR3 = I3 – J3 = 0,540 – 1 = - 0,46 A;
IR4 = I4 – J4 = 0,578 - 0,5 = 0,078 A;
I5 = I4 – I3 = 0,578 -0,540 = 0,038 A.
Расчёт потенциалов узлов:
>> GB=[1/4 1/6 1/2 1/8 1/10]
GB =
0.2500 0.1667 0.5000 0.1250 0.1000 - проводимости ветвей
>> G=diag(GB)
G =
0.2500 0 0 0 0
0 0.1667 0 0 0 - диагональная матрица
0 0 0.5000 0 0 проводимостей ветвей
0 0 0 0.1250 0
0 0 0 0 0.1000
>> GY=A*G*A'
GY =
0.9167 -0.5000 - матрица узловых
-0.5000 0.7250 проводимостей
>> JY=A*J-A*G*E
JY =
2.4167 - матрица узловых токов
-1.6000
>> fu=GY^(-1)*JY - матрица узловых потенциалов
fu =
2.2965 потенциал первого узла
-0.6231 потенциал второго узла
>> fu=GY\JY
fu =
2.2965
-0.6231
>> fu=inv(GY)*JY
fu =
2.2965
-0.6231
Таким образом, если А – матрица коэффициентов системы уравнений размерностью n×n, В – вектор – столбец свободных членов размерностью n×1, х – вектор – столбец неизвестных размерностью n×1, то решение системы уравнений А*х = В возможно по одному любому из следующих выражений: x = inv(A)*B; x =A\B и x = A-1*B при условии, что det(A) ≠ 0.
Решение систем линейных уравнений возможно также с помощью функций solve ( ). Например, требуется решить систему уравнений
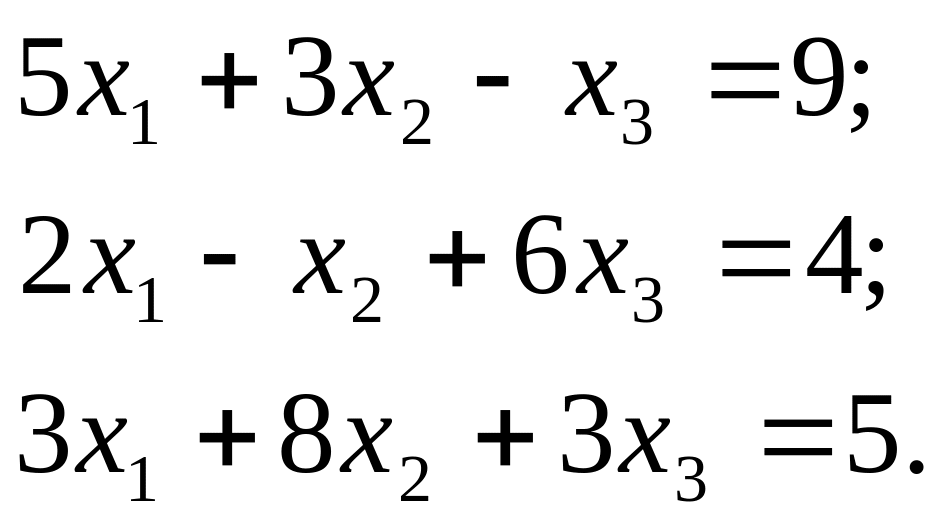
>> syms x1 x2 x3; - определение символьных переменных
>> X=solve('5*x1+3*x2-x3=9','2*x1-x2+6*x3=4','3*x1+8*x2+3*x3=5')
X =
x1: [1x1 sym]
x2: [1x1 sym]
x3: [1x1 sym]
>> X.x1 - вывод решения
ans =
13/7
>> X.x2
ans =
-10/119
>> X.x3
ans =
4/119
>> vpa(X.x1,4) - вывод решения с заданным числом знаков ответа
ans =
1.857
>> vpa(X.x2,4)
ans =
-.8403e-1
>> vpa(X.x3,4)
ans =
.3361e-1
Если матрица А – разрежённая матрица, то целесообразно применять итерационные методы (метод наименьших квадратов, сопряжённых градиентов и др.) решения таких систем уравнений и соответствующих им функций. Эти же функции применяются и для решения обычных систем линейных алгебраических уравнений:
bccg( ) – двунаправленный метод сопряжённых градиентов
>> x1=bicg(A,B); - выдаёт результат с погрешностью по умолчанию 10-6
bicg converged at iteration 3 to a solution with relative residual 8.1e-016
>> x2=bicg(A,B,0.0001); - выдаёт результат с заданной погрешностью
bicg converged at iteration 3 to a solution with relative residual 8.1e-016
>> x3=bicg(A,B,0.0001,15); - выдаёт результат с заданной погрешностью
при заданном числе итераций
bicg converged at iteration 3 to a solution with relative residual 8.1e-016
>> X=[x1,x2,x3]
X =
1.8571 1.8571 1.8571
-0.0840 -0.0840 -0.0840
0.0336 0.0336 0.0336
во всех случаях получен одинаковый ответ;
cgs( ) – квадратичный метод сопряжённых градиентов
>> cgs(A,B)
cgs converged at iteration 3 to a solution with relative residual 3.3e-015
ans =
1.8571
-0.0840
0.0336
pcg( ) – метод сопряжённых градиентов
>> pcg(A,B)
pcg stopped at iteration 3 without converging to the desired tolerance 1e-006
because the maximum number of iterations was reached.
The iterate returned (number 2) has relative residual 0.44
ans =
2.0856
0.3726
-0.0385
bicgstab( ) – устойчивый двунаправленный метод
>> bicgstab(A,B)
bicgstab converged at iteration 2.5 to a solution with relative residual 1.8e-016
ans =
1.8571
-0.0840
0.0336
lsqr( ) – метод наименьших квадратов
>> lsqr(A,B)
lsqr stopped at iteration 3 without converging to the desired tolerance 1e-006
because the maximum number of iterations was reached.
The iterate returned (number 3) has relative residual 1.6e-015
ans =
1.8571
-0.0840
0.0336
gmres( ) – метод минимизации обобщённой невязки
>> gmres(A,B)
gmres converged at iteration 3 to a solution with relative residual 8e-017
ans =
1.8571
-0.0840
0.0336
qmr( ) – квазиминимизация невязки
>> qmr(A,B)
qmr converged at iteration 3 to a solution with relative residual 2e-016
ans =
1.8571
-0.0840
0.0336
Более подробное описание этих функций приведено в [4].
Эти же функции можно применять при расчётах электрических цепей символическим методом (решение систем линейных алгебраических уравнений с комплексными коэффициентами):
>> A=[1+2i -4+4i 0+i;-4-10i 5+5i 10+i;5+i 7+5i 9-5i]
A =
1.0000 + 2.0000i -4.0000 + 4.0000i 0 + 1.0000i
-4.0000 -10.0000i 5.0000 + 5.0000i 10.0000 + 1.0000i
5.0000 + 1.0000i 7.0000 + 5.0000i 9.0000 - 5.0000i
>> B= [100+60i;220-100i;-50i]
B =
1.0e+002 *
1.0000 + 0.6000i
2.2000 - 1.0000i
0 - 0.5000i
>> X=A\B
X =
-7.1841 +17.7280i
-11.2561 -26.7692i
-5.4121 + 9.4609i
>> lsqr(A,B)
lsqr stopped at iteration 3 without converging to the desired tolerance 1e-006
because the maximum number of iterations was reached.
The iterate returned (number 3) has relative residual 5.1e-015
ans =
-7.1841 +17.7280i
-11.2561 -26.7692i
-5.4121 + 9.4609i
Порядок выполнения работы
1. Для электрической цепи, заданной в виде графа (рис. 5), записать матрицы соединений, главных контуров, источников ЭДС и токов, диагональные матрицы сопротивлений и проводимостей ветвей. Номиналы элементов схем приведены в таблице 1, 2.
2. Решить матричные уравнения метода контурных токов и узловых потенциалов с помощью различных операторов. Токи сопротивлений проверить по уравнению энергетического баланса.
Вопросы для самопроверки
1. Приведите примеры линейных элементов электрических цепей и их
математических моделей.
2. Как формируются матрицы инциденций и главных контуров?
3. Какие операторы используются для решения систем линейных
алгебраических уравнений?
4. При каких условиях система линейных алгебраических уравнений имеет
решение?
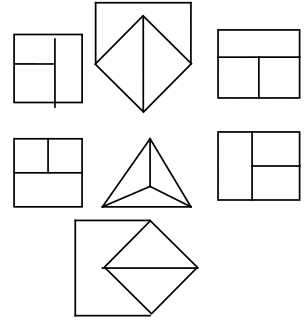
2 3
1 2 3
1 3 1 2
а) 4 б) 4 в) 4
1
2 1
3
1 4 2 4
4
г) 3 2 3 е)
1 д)
2 4
3
ж)
Рис. 1
Таблица 1
Ветвь |
Граф схемы |
|||||||||||||
а |
б |
в |
г |
д |
е |
ж |
||||||||
узлы |
узлы |
узлы |
узлы |
узлы |
узлы |
узлы |
||||||||
1 |
1 |
2 |
2 |
3 |
3 |
4 |
3 |
2 |
3 |
4 |
4 |
1 |
4 |
3 |
2 |
1 |
3 |
4 |
2 |
2 |
1 |
1 |
3 |
1 |
4 |
2 |
4 |
1 |
3 |
3 |
1 |
4 |
3 |
1 |
3 |
2 |
3 |
4 |
4 |
2 |
4 |
3 |
2 |
1 |
4 |
2 |
3 |
1 |
4 |
4 |
1 |
1 |
4 |
1 |
2 |
3 |
1 |
3 |
2 |
5 |
4 |
3 |
3 |
4 |
4 |
2 |
2 |
1 |
2 |
3 |
1 |
2 |
1 |
4 |
6 |
2 |
4 |
2 |
1 |
3 |
1 |
2 |
4 |
3 |
1 |
3 |
2 |
4 |
2 |
Таблица 2
№ |
R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
RV |
|
Ом |
||||||
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
5 8 3 7 2 9 10 6 7 8 6 5 8 3 5 8 4 3 2 9 6 7 8 5 8 |
25 23 21 32 16 18 16 24 27 17 13 19 12 21 24 23 25 29 14 15 13 18 17 15 19 |
20 19 12 14 16 18 17 19 15 13 11 27 21 13 18 17 18 19 22 27 21 17 25 14 12 |
11 9 7 9 5 7 10 11 12 16 8 14 9 11 14 7 8 9 5 9 10 9 6 7 8 |
19 20 21 22 23 18 15 13 12 14 16 18 19 20 6 16 14 18 12 22 21 18 16 14 15 |
14 13 12 11 10 11 12 13 14 15 10 9 17 15 10 11 9 10 8 19 18 21 12 21 22 |
100 150 120 130 90 100 110 130 120 200 160 140 180 170 100 120 200 120 190 140 150 160 170 180 190 |
Таблица 3
№ |
Е1 |
Е3 |
Е5 |
J1 |
J4 |
J6 |
B |
A |
|||||
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
-50 25 44 28 -31 66 -46 54 -12 19 22 24 -28 37 34 39 -50 28 19 24 -36 38 44 27 -31 |
10 -12 14 -16 18 -20 19 -17 15 -13 11 -10 12 -14 16 -18 20 -21 19 -17 15 -13 11 -13 15 |
31 29 -27 25 23 21 -19 20 22 24 -26 28 30 31 -19 117 21 23 -25 27 29 18 -16 34 24 |
1 0.5 1 -1.5 1.2 -0.4 0.7 -2 1.3 -1.5 -1.1 1.3 1 -1.3 0.5 0.8 0.9 1 -1.8 1.4 -1.2 2 -2.1 1.1 -1.4 |
0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 |
1 0 1 0 0.5 0 0.6 0 1 0 0.6 0 0.4 0 0.3 0 0.2 0 0.1 0 0.8 0 0.5 0 0.7 |